在工程实践中,经常遇到类似的问题:
我们做了n次实验,获得了一组数据
然后,我们希望知道x和y之间的函数关系。所以我们将其描绘在XOY直角坐标系下,得到下面这么一张点云图:
然后,我们发现,x和y「可能」是线性的关系,因为我们可以用一条直线大致的将所有的样本点串连起来,如下图:
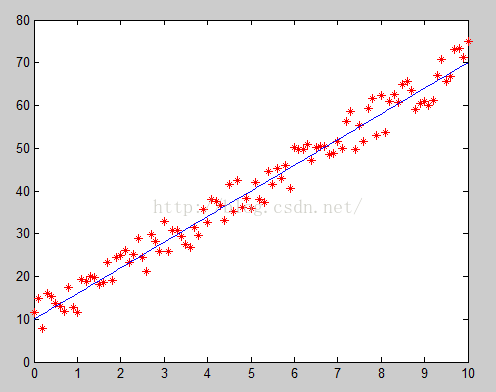
所以,我们可以「猜测」。接下来的问题,就是求出a和b的值。
这看起来是一个很简单的问题,a和b是两个未知数,我们只需要随意找出两个样本点,列出方程组:
两个未知数,两个方程,就可以求解出a和b的值。
然而,在这里是不对的,或者说是不准确的。为什么呢?因为 这个函数关系,是我们「猜测」的,并不一定是客观正确的(虽然也许是正确的)。所以我们不能这么简单粗暴的方程组求解。
那怎么办呢?既然是「猜测」的,那么就存在误差。那么我们将这个函数关系稍加修正为:
这里, 分别是第i次实验的因变量、自变量、误差。
既然是「猜测」,那我们当然希望猜得准一点。那怎么衡量准确呢?自然和e有关系。
上式变型后可得:
在这里,a和b才是自变量,e是函数值。
这里是最容易搞糊涂的地方,为什么a,b是自变量,而不是x,y?
这就要提及「曲线拟合」的概念。所谓「拟合」就是说我们要找到一个函数,来「匹配」我们在实验中获得的样本值。放到上面的例子,就是我们要调整a和b的值,来使得这个函数和实验中获得的数据更加「匹配」。所以,a和b才是「曲线拟合」过程中的自变量。
接下来,继续如何让误差更小的问题。
「最小二乘法」的思想核心,就是定义一个损失函数:
显然,如果我们调整a和b,使得Q达到最小,那么「曲线拟合」的误差也会最小。
这里,Q是a,b的函数。根据高等数学的只是,Q的最小值点必然是其导数为0的点。
所以,我们令:
求解上述方程组,则可以解得a和b的值。这就是最小二乘法的整个过程。
最后说明:
(1)最小二乘法英文名Least Squares,其实翻译成「最小平方法」,更容易让人理解。其核心就是定义了损失函数;
(2)评价误差的方法不止一个,还有诸如 等(当然这就不是最小二乘法了);
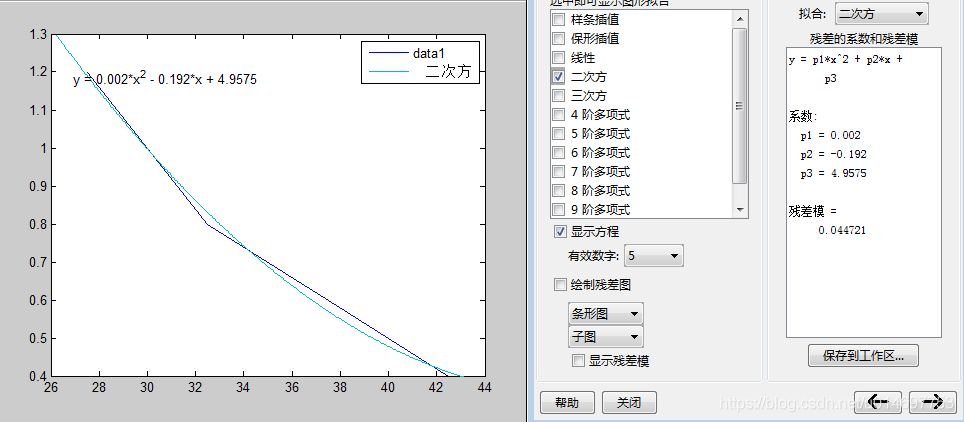
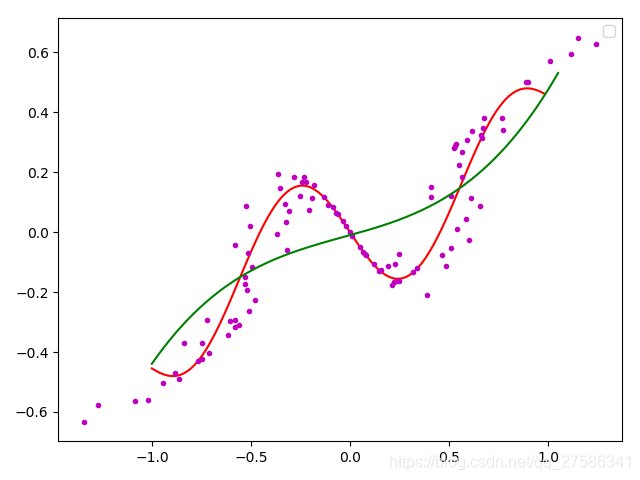
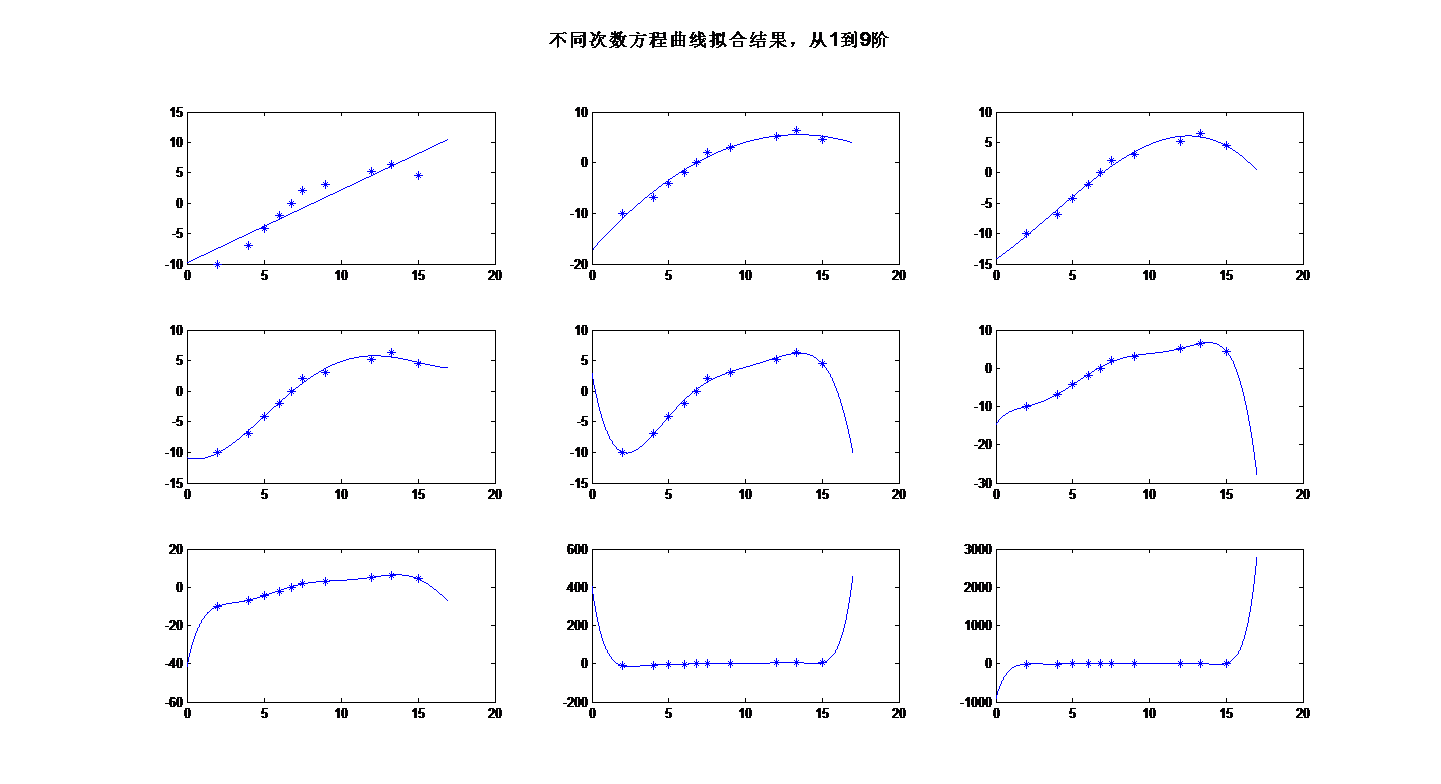
(3)最小二乘法不仅可以用于一次函数的拟合,还可以用于更高次函数的拟合;
(4)最小二乘法既是一种曲线拟合的方法,也可用于最优化。