最小二乘法曲线拟合原理

一、最小二乘法原理

对于给定的一组数据（xi,yi），假定它满足n次多项式：
在这里插入图片描述
为了求取各阶参数的最优解，对于每个xi，通过n次多项式计算的值和yi之间的差值的平方和应该最小，即：

由于其拟合函数为多项式，这样的曲线拟合问题又叫多项式拟合问题，特别的，当n=1时，一次多项式拟合又叫直线拟合。将a0，a1…an作为变量，对上式进行偏分求导，得到n+1组方程：
在这里插入图片描述
可以简化为：MA=B，则A=M-1B；或者通过消元法求解各个a的值。其中：

二、最小二乘法矩阵表示

对于给定的一组数据（x1,y1），其矩阵表示为：
在这里插入图片描述
对于m个点对来说，可以组合成矩阵的模式：

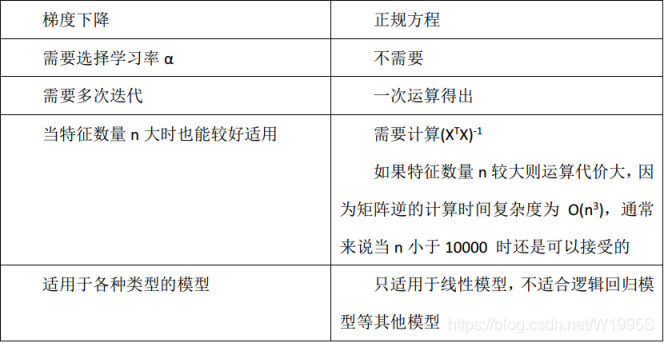
利用矩阵表示为XA=Y，其中此种超定方程的最小二乘解为：

三、代码实现（基于第一种表示）

以两次多项式为例，各阶求和函数，2阶：

double average2(double* x0, double* y0, int Num)
{	double addsum = 0;double addaverage = 0;	for (int i = 0; i < Num; i++)	{				addsum = addsum + x0[i] * y0[i];}addaverage = addsum / Num;	return addaverage;
}

3阶：

double average3(double* x0, double* y0, double* z0, int Num)
{double addsum = 0;	double addaverage = 0;	for (int i = 0; i < Num; i++)	{ addsum = addsum + x0[i] * y0[i] * z0[i]; 	}	addaverage = addsum / Num;	return addaverage;
}

其它阶次的函数可参考实现。多项式系数求解：

bool calcPolFit2(double * ValidX, double * ValidY, int Num)
{int validNum = Num;	arma::mat matM(3, 3);	arma::vec matB(3, 1);	arma::vec result(3, 1);//组织矩阵M	matM(0, 0) = average4(ValidX, ValidX, ValidX, ValidX, validNum);	matM(0, 1) = average3(ValidX, ValidX, ValidX, validNum);	matM(0, 2) = average2(ValidX, ValidX, validNum);	matM(1, 0) = matM(0, 1);	matM(1, 1) = matM(0, 2);	matM(1, 2) = average1(ValidX, validNum);	matM(2, 0) = matM(0, 2);	matM(2, 1) = matM(1, 2);	matM(2, 2) = 1;//组织矩阵B	matB(0) = average3(ValidX, ValidX, ValidY, validNum);	matB(1) = average2(ValidX, ValidY, validNum);	matB(2) = average1(ValidY, validNum);	result = inv(matM)*matB;	A = result(0);	B = result(1);	C = result(2);		return true;
}