最小二乘法曲线拟合以及Matlab实现
在实际工程中,我们常会遇到这种问题:已知一组点的横纵坐标,需要绘制出一条尽可能逼近这些点的曲线(或直线),以进行进一步进行加工或者分析两个变量之间的相互关系。而获取这个曲线方程的过程就是曲线拟合。
目录
- 最小二乘法直线拟合原理
- 曲线拟合
- Matlab实现代码
最小二乘法直线线拟合原理
首先,我们从曲线拟合的最简单情况——直线拟合来引入问题。如果待拟合点集近似排列在一条直线上时,我们可以设直线 y = a x + b y=ax+b y=ax+b 为其拟合方程,系数 A = [ a , b ] A=[a,b] A=[a,b] 为待求解项,已知:
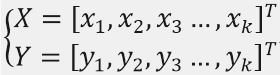 。
。
用矩阵形式表达为: Y = X 0 A Y=X_{0}A Y=X0A,其中:
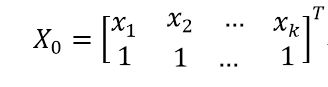
要求解A,可在方程两边同时左乘 X 0 X_{0} X0 的逆矩阵,如果它是一个方阵且非奇异的话。
但是,一般情况下 X 0 X_{0} X0 连方阵都不是,所以我们在此需要用 X 0 X_{0} X0 构造一个方阵,即方程两边同时左乘 X 0 X_{0} X0 的转置矩阵,得到方程: X 0 T Y = X 0 T X 0 A X_{0}^{T}Y=X_{0}^{T}X_{0}A X0TY=X0TX0A 。
此时,方程的系数矩阵 X 0 T X 0 X_{0}^{T}X_{0} X0TX0 为方阵,所以两边同时左乘新系数矩阵 X 0 T X 0 X_{0}^{T}X_{0} X0TX0 的逆矩阵,便可求得系数向量A ,即: ( X 0 T X 0 ) − 1 X 0 T Y = A (X_{0}^{T}X_{0})^{-1}X_{0}^{T}Y=A (X0TX0)−1X0TY=A 。
方程 A = ( X 0 T X 0 ) − 1 X 0 T Y A=(X_{0}^{T}X_{0})^{-1}X_{0}^{T}Y A=(X0TX0)−1X0TY 右边各部分均已知,所以可直接求解得到拟合直线的方程系数向量A。
曲线线拟合
当样本点的分布不为直线时,我们可用多项式曲线拟合,即拟合曲线方程为n阶多项式
y = ∑ i = 0 n a i x i = a n x n + a n − 1 x n − 1 + . . . + a 1 x + a 0 y=\sum_{i=0}^{n}a_ix^i=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0 y=∑i=0naixi=anxn+an−1xn−1+...+a1x+a0 。
用矩阵形式表示为: Y = X 0 A Y=X_0A Y=X0A ,其中:

待求解项为系数向量 A = [ a n , a n − 1 , . . . , a 2 , a 1 , a 0 ] T A=[a_n,a_{n-1},...,a_2,a_1,a_0]^T A=[an,an−1,...,a2,a1,a0]T。
曲线拟合方程 Y = X 0 A Y=X_0A Y=X0A 的求解方法与上面直线的求解方法一样,也是在方程 Y = X 0 A Y=X_0A Y=X0A 两边同左乘 X 0 X_0 X0的转置矩阵得到: X 0 T Y = X 0 T X 0 A X_{0}^{T}Y=X_{0}^{T}X_{0}A X0TY=X0TX0A,
再同时在新方程两边同时左乘 X 0 T X 0 X_{0}^{T}X_{0} X0TX0 的逆矩阵,得到: ( X 0 T X 0 ) − 1 X 0 T Y = A (X_{0}^{T}X_{0})^{-1}X_{0}^{T}Y=A (X0TX0)−1X0TY=A
上式左边各部分均已知,所以可直接求解得拟合曲线方程的系数向量A。
Matlab实现代码
%by hanlestudy@163.com
clear
clc
x=[2,4,5,6,6.8,7.5,9,12,13.3,15];
y=[-10,-6.9,-4.2,-2,0,2.1,3,5.2,6.4,4.5];
[~,k]=size(x);
for n=1:9X0=zeros(n+1,k);for k0=1:k %构造矩阵X0for n0=1:n+1X0(n0,k0)=x(k0)^(n+1-n0);endendX=X0';ANSS=(X'*X)\X'*y';for i=1:n+1 %answer矩阵存储每次求得的方程系数,按列存储answer(i,n)=ANSS(i);endx0=0:0.01:17;y0=ANSS(1)*x0.^n ;%根据求得的系数初始化并构造多项式方程for num=2:1:n+1 y0=y0+ANSS(num)*x0.^(n+1-num);endsubplot(3,3,n)plot(x,y,'*')hold onplot(x0,y0)
end
suptitle('不同次数方程曲线拟合结果,从1到9阶')
运行结果
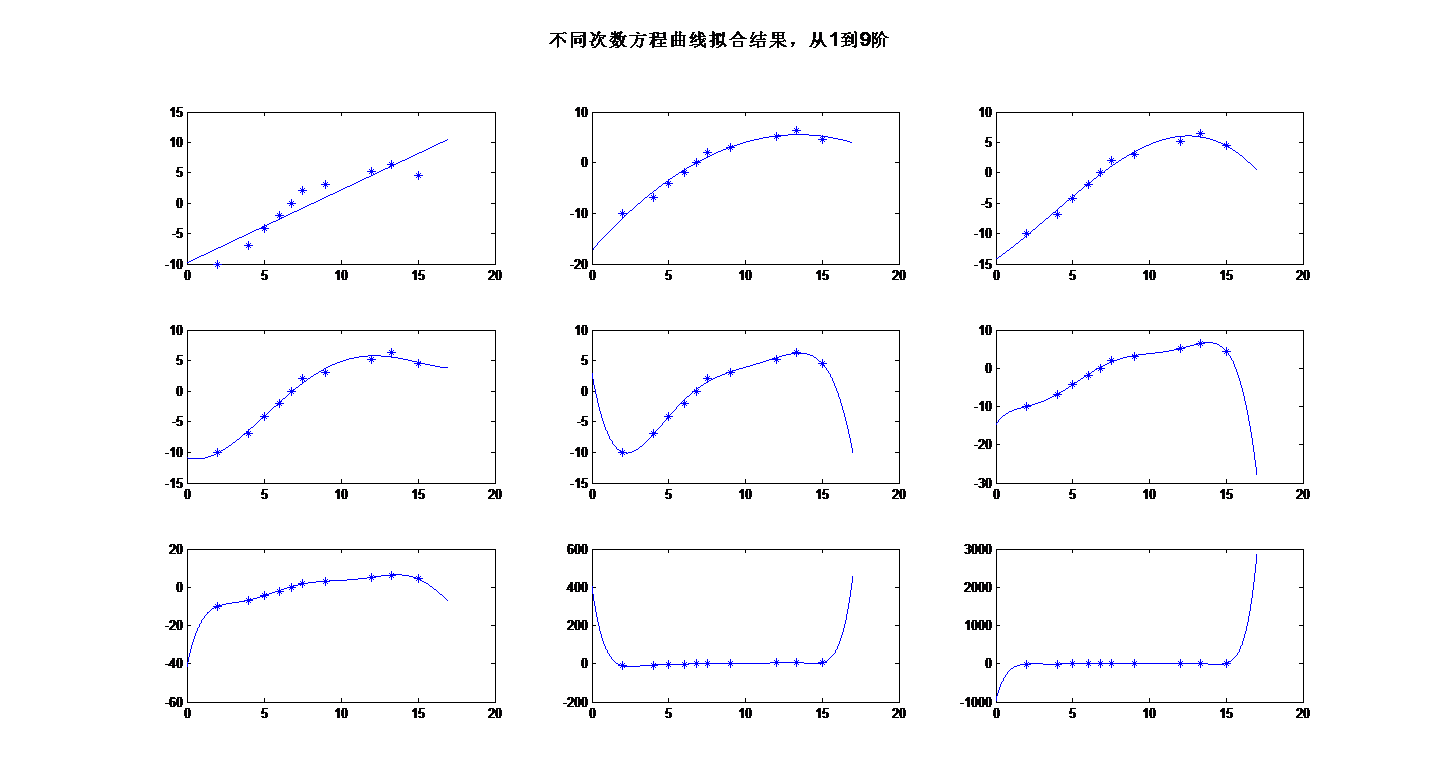
拟合曲线结果:
可以看出看来,当多项式的阶数过小是,曲线并不能很好地反映出样本点的分布情况;但阶数过高时,会出现过拟合的情况。
系数矩阵answer:
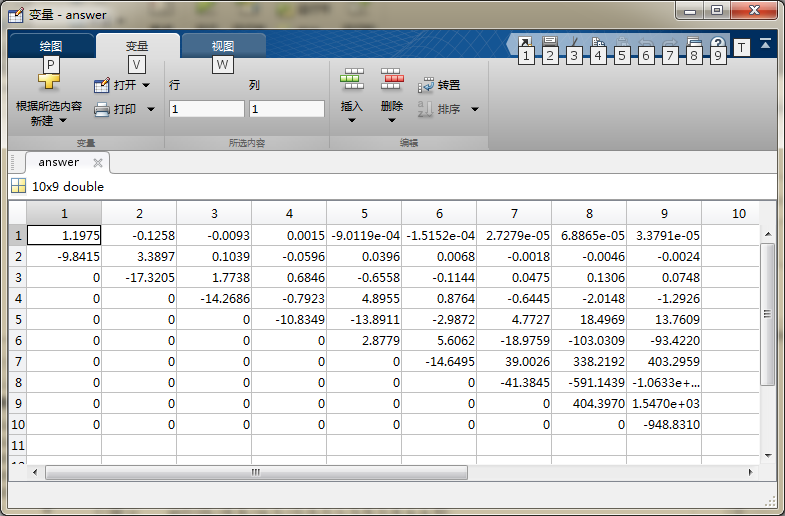
Matlab自带函数——polyfit
在matlab中,也有现成的曲线拟合函数polyfit,其也是基于最小二乘原理实现的,具体用法为:ans=polyfit(x,y,n). 其中x,y为待拟合点的坐标向量,n为多项式的阶数。
下面代码是用polyfit函数来做曲线拟合:
clear
clc
x=[2,4,5,6,6.8,7.5,9,12,13.3,15];
[~,k]=size(x);
y=[-10,-6.9,-4.2,-2,0,2.1,3,5.2,6.4,4.5];
for n=1:9ANSS=polyfit(x,y,n); %用polyfit拟合曲线for i=1:n+1 %answer矩阵存储每次求得的方程系数,按列存储answer(i,n)=ANSS(i);endx0=0:0.01:17;y0=ANSS(1)*x0.^n ; %根据求得的系数初始化并构造多项式方程for num=2:1:n+1 y0=y0+ANSS(num)*x0.^(n+1-num);endsubplot(3,3,n)plot(x,y,'*')hold onplot(x0,y0)
end
suptitle('不同次数方程曲线拟合结果,从1到9阶')
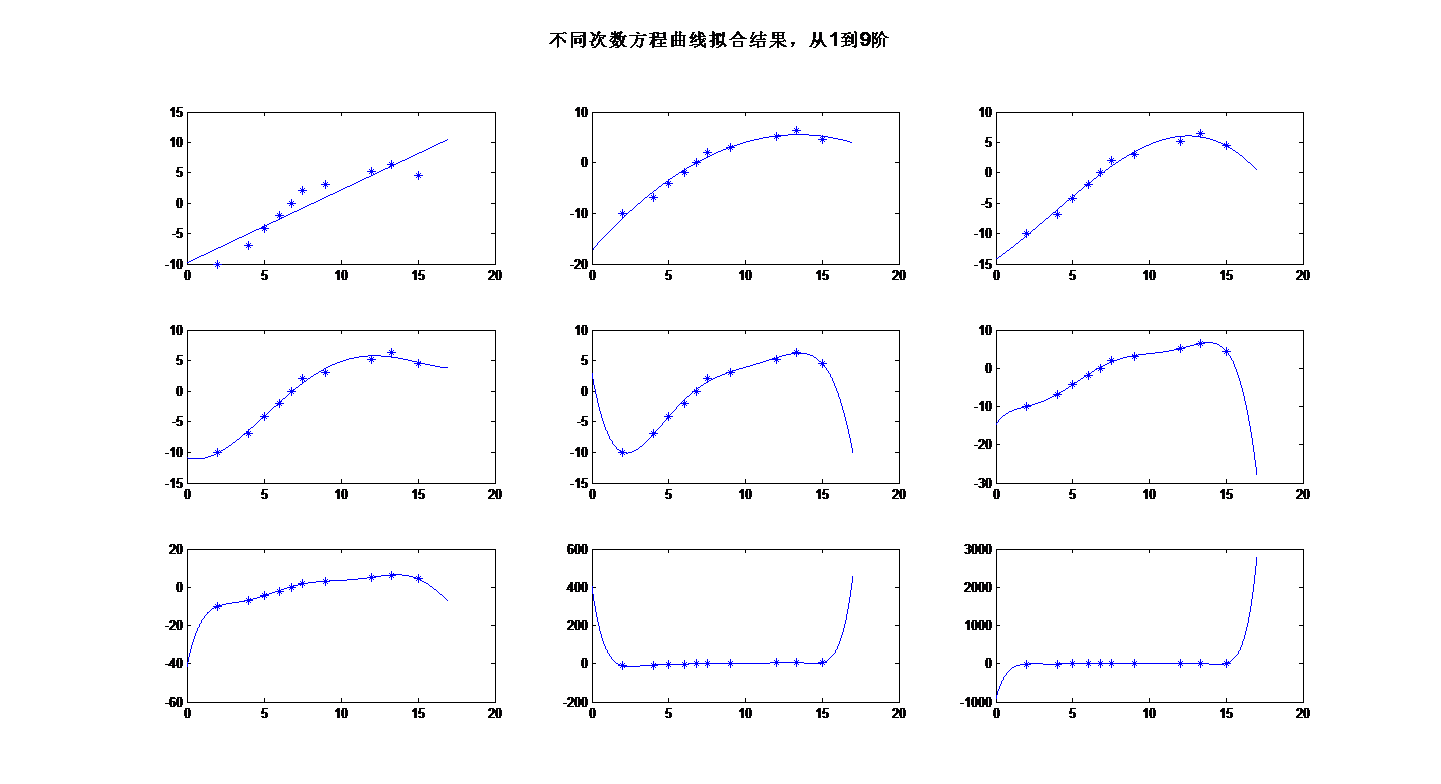
运行结果:
用polyfit拟合的结果与第一份代码运行的结果基本一样
申明
本文为本人原创,转载请注明出处!