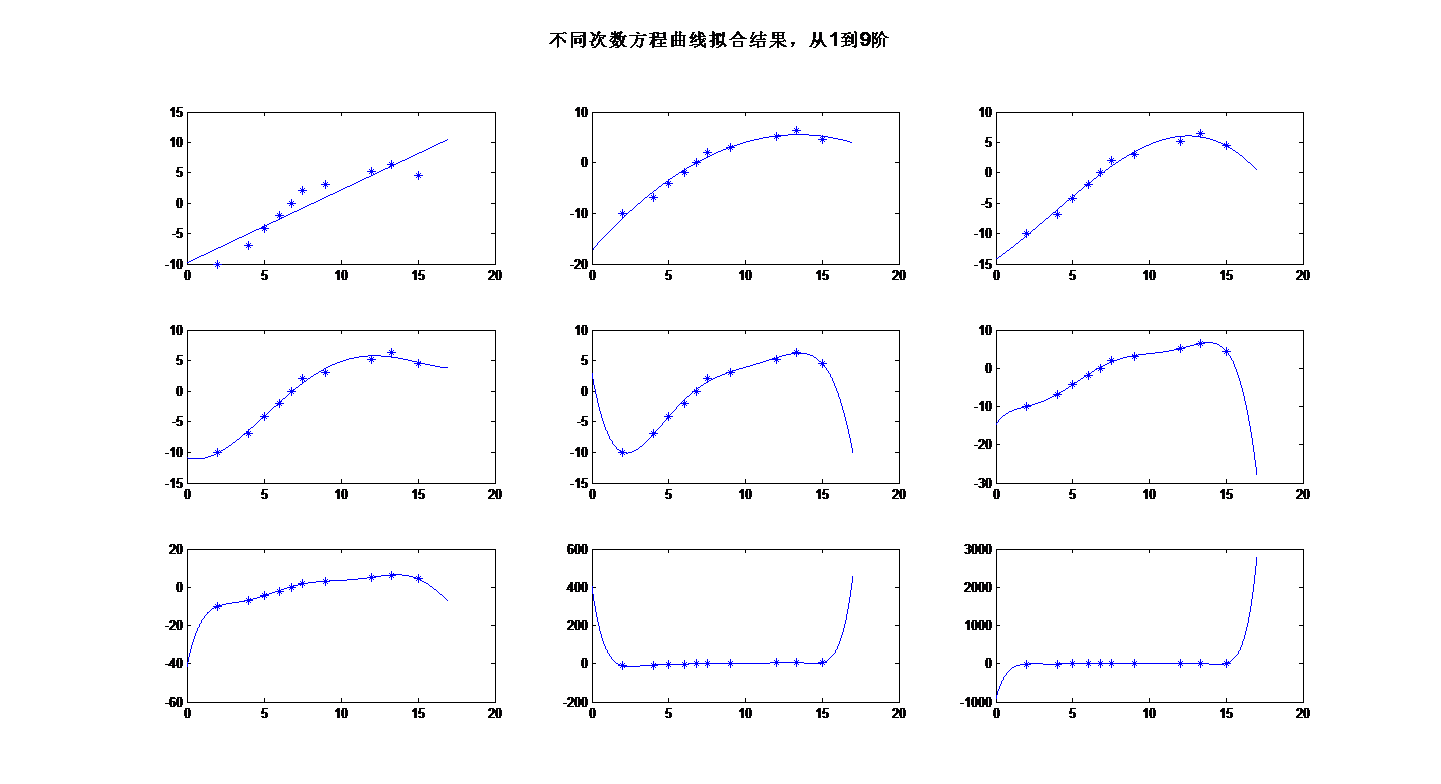
原文链接：https://www.jianshu.com/p/1c4f3edbaa47

首先最小二乘法是面对不连续的离散点。

它的本质是求某些参数，估计值在整体下可以使误差ε最小。

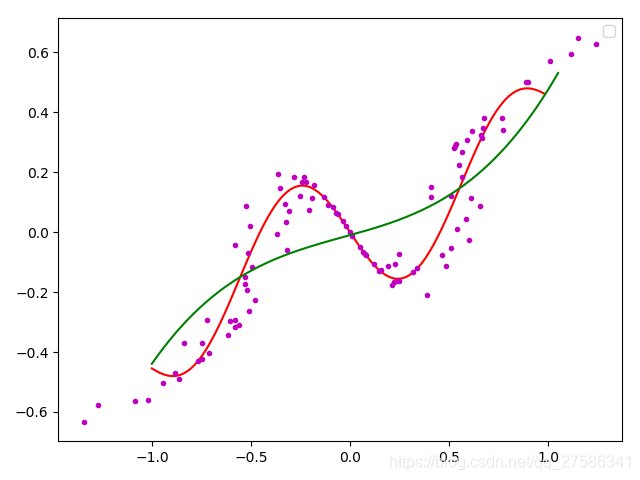
对于离散点的直线拟合、曲线拟合是在满足误差最小的基础上，得出可以用数学函数式表达的可视化线图。

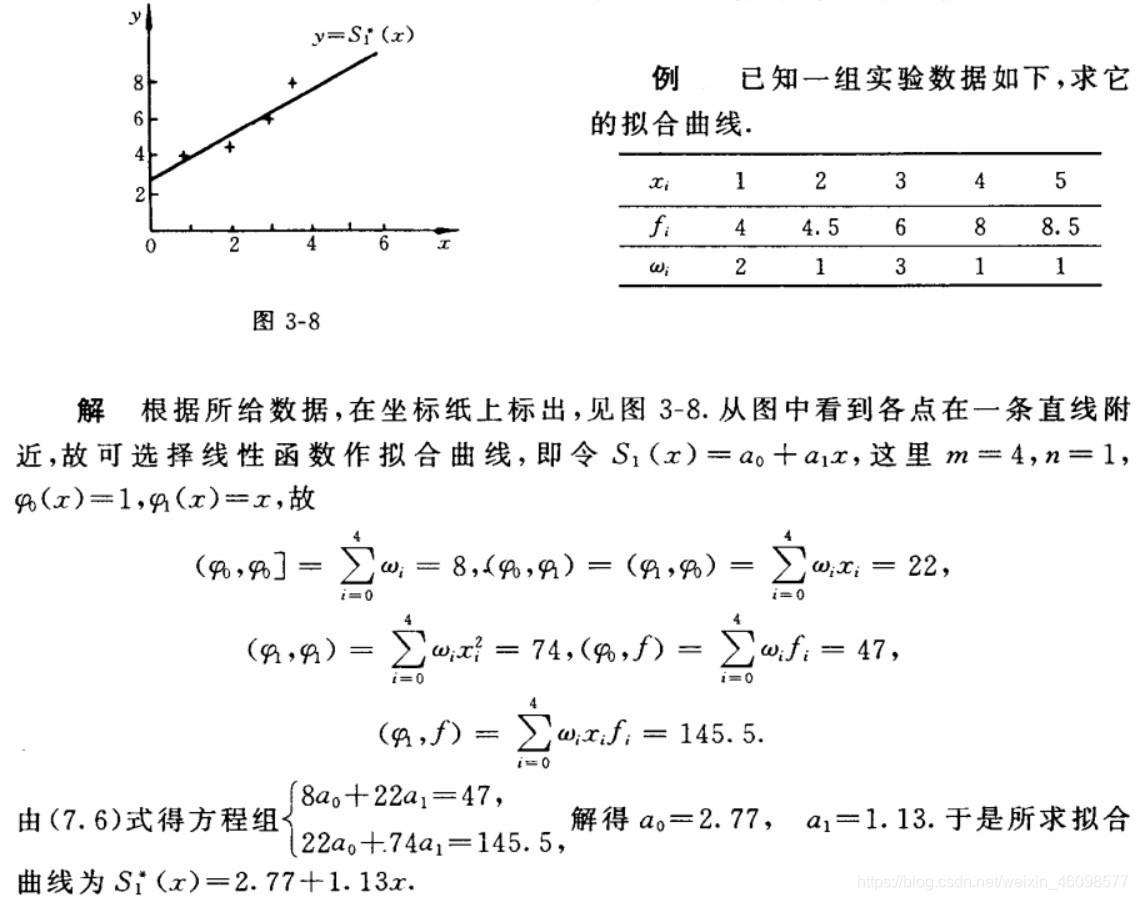
直线拟合的例子：

天气温度和冰淇淋销量的关系图：

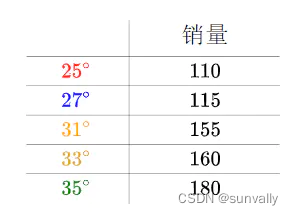
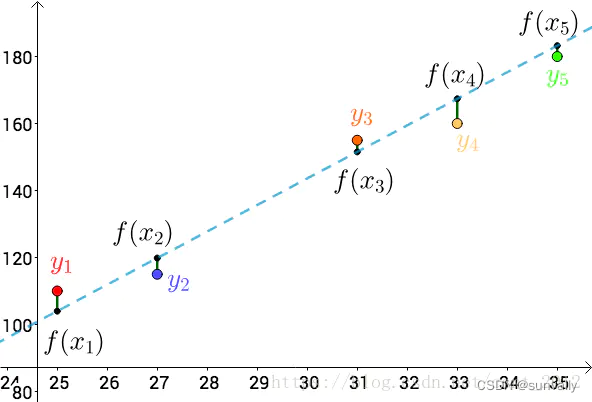
标记在坐标轴上：

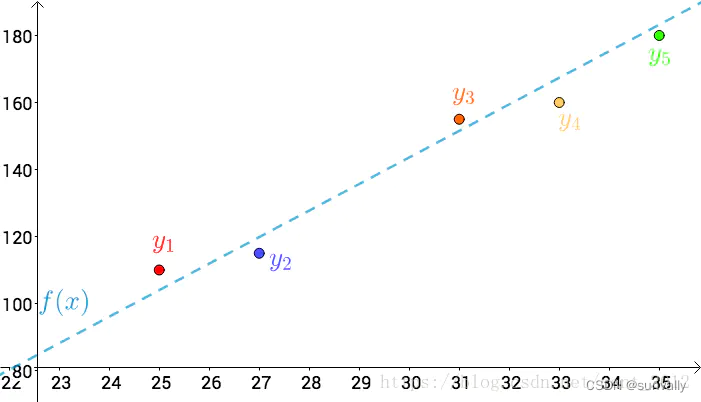
假设这种线性关系为：f(x)=ax+b

分别标号：i,x,y

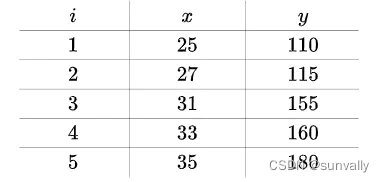
总误差的平方为：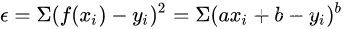
通过最小二乘法的思想：

在误差式子中，不同的a,b会导致不同的\epsilon ，根据多元微分的知识，

当它们的偏微分等于0时，\epsilon 可取最小值。

上述方程组为线性方程组，求解方程组，得出a,b的值。

求得函数图像为：

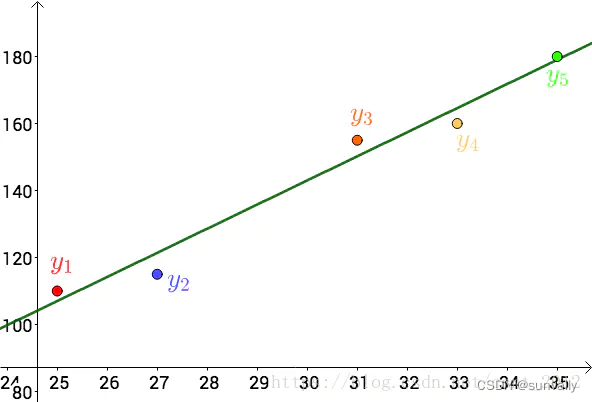
以上是直线拟合的主线步骤。

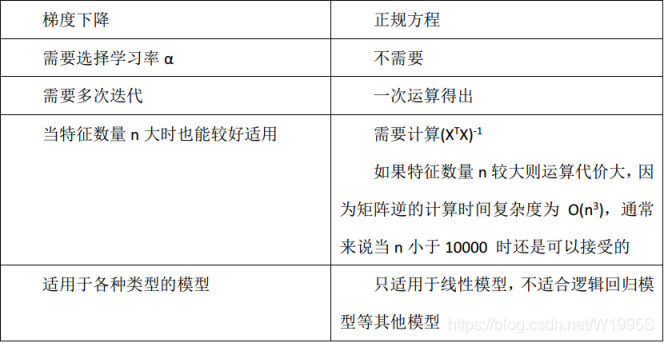
对于如何求解线性方程组，接下来我们一块学习。

拟合直线函数：

1、表示X,Y的向量

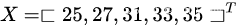
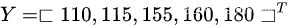
2、函数参数向量

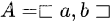
3、构造矩阵X0

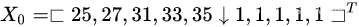
4、矩阵等式

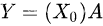
5、对矩阵构造方阵

方程两边同时左乘X0的转置矩阵，得到方程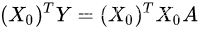

6、求系数向量

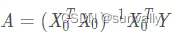
作者：KingKit
链接：https://www.jianshu.com/p/1c4f3edbaa47
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。