1 什么是最小二乘

在科学实验的统计方法研究中，往往要从一组实验数据 $(x_i,y_i)(i=0,1,2,\dots ,m)$ 中寻找自变量 $x$ 与因变量 $y$ 之间的函数关系 $y=F(x)$. 由于观测数据往往不准确，因此不要求 $y=F(x)$ 经过所有点$(x_i,y_i)$，而只要求在给定点 $x_i$ 上误差${\delta }_i=F(x_i)-y_i(i=0,1,2,\dots ,m)$按某种标准最小。若记 $\delta =({\delta }_0,{\delta }_1,\dots ,{\delta }_m{)}^T$，就是要求向量 $\delta$ 的范数最小，通常采用计算较为简单的欧式范数 $\Vert \delta {\Vert }_2$ 作为误差衡量的标准。

关于最小二乘的一般提法是：对给定的一组数据 $(x_i,y_i)(i=0,1,2,\dots ,m)$，要求在函数类 φ { φ 0 , φ 1 , … , φ n } φ\{φ_0,φ_1,…,φ_n\} φ{φ0​,φ1​,…,φn​}中找到一个函数 $y=S^{\ast }(x)$，使误差平方和最小，即
$$\Vert \delta {\Vert }_2^2=\sum _{i=0}^m{\delta }_i^2=\sum _{i=0}^m[S^{\ast }(x_i)-y_i{]}^2=mi{n}_{S(x)\in \phi }\sum _{i=0}^m[S(x_i)-y_i{]}^2----(Formula.1)$$

其中，
$$S(x)=a_0{\phi }_0(x)+a_1{\phi }_1(x)+\cdots +a_1{\phi }_1(x),(n<m)----(Formula.2)$$

这就是一般的最小二乘逼近，用几何语言说，就称为曲线拟合的最小二乘法。

2 最小二乘原理

用最小二乘法求拟合曲线时，首先要确定 $S(x)$ 的形式。这不单纯是数学问题，还与所研究问题的运动规律及所得观测数据 $(x_i,y_i)$ 有关；通常要从问题的运动规律及给定数据描图，确定 $S(x)$ 的形式，并通过实际计算选出较好的结果。$S(x)$的一般表达式为 $Formula.2$ 式表示的线性形式。为了使问题的提法更有一般性，通常把最小二乘法中$\Vert \delta {\Vert }_2^2$都考虑为加权平方和
$$\Vert \delta {\Vert }_2^2=\sum _{i=0}^m\omega (x_i){\left[S(x_i)-f(x_i)\right]}^2----(Formula.3)$$
这里，$\omega (x)\ge 0$是$[a,b]$上的权函数，它表示不同点$(x_i,f(x_i))$处的数据比重不同，通常表示在点 $(x_i,f(x_i))$ 处重复观测的次数。用最小二乘法求拟合曲线的问题，就是在形如 $(Formula.2)$ 式的 $S(x)$ 中求一函数 $y=S^{\ast }(x)$，使 $Formula.3$ 式取得最小。可以将这个问题转化为求多元函数
$$I(a_0,a_1,\dots ,a_n)=\sum _{i=0}^m\omega (x_i){\left[\sum _{j=0}^n{a}_j{\phi }_j(x_i)-f(x_i)\right]}^2-----(Formula.4)$$
的极小值点 $(a_0^{\ast },a_1^{\ast },\dots ,a_n^{\ast })$ 的问题。

由求多元函数极值的必要条件，有
$$\frac{\partial I}{\partial a_k}=2\sum _{i=0}^m\omega (x_i)\left[\sum _{j=0}^n{a}_j{\phi }_j(x_i)-f(x_i)\right]{\phi }_k(x_i)=0,(k=0,1,\dots ,n)----(Formula.5)$$
若记
$$({\phi }_j,{\phi }_k)=\sum _{i=0}^m\omega (x_i){\phi }_j(x_i){\phi }_k(x_i)----(Formula.6)$$
$$(f,{\phi }_k)=\sum _{i=0}^m\omega (x_i)f(x_i){\phi }_k(x_i)\equiv d_k,(k=0,1,\dots ,n)----(Formula.7)$$
则 $Formula.4$ 可改写为
$$\sum _{j=0}^n({\phi }_k,{\phi }_j)a_j=d_k,(k=0,1,\dots ,n)----(Formula.8)$$
$Formula.8$ 式称为法方程，矩阵形式为
$$Ga=d----(Formula.9)$$
其中，$a=(a_0,a_1,...,a_n{)}^T$，$d=(d_0,d_1,...,d_n{)}^T$
$$G=\left[\begin{array}{cccc}({\phi }_0,{\phi }_0)& ({\phi }_0,{\phi }_1)& \cdots & ({\phi }_0,{\phi }_n)\\ ({\phi }_1,{\phi }_0)& ({\phi }_1,{\phi }_1)& \cdots & ({\phi }_1,{\phi }_n)\\ ⋮& ⋮& \ddots & ⋮\\ ({\phi }_n,{\phi }_0)& ({\phi }_n,{\phi }_1)& \cdots & ({\phi }_n,{\phi }_n)\end{array}\right]$$
由于 ${\phi }_0,{\phi }_1,...,{\phi }_n$ 线性无关，因此 $|G|\ne 0$，方程组 $Formula.8$ 存在唯一解
$$a_k=a_k^{\ast }，（k=0,1,...,n）----(Formula.10)$$
从而得到函数 $f(x)$ 的最小二乘解为
$$S^{\ast }(x)=a_0^{\ast }{\phi }_0(x)+a_1^{\ast }{\phi }_1(x)+...+a_n^{\ast }{\phi }_n(x)----(Formula.11)$$
可以证明 $S^{\ast }(x)$ 对于任何形如 $Formula.2$ 式的 $S(x)$ ，都有
$$\sum _{i=0}^m\omega (x_i)[S^{\ast }(x_i)-f(x_i){]}^2\le \sum _{i=0}^m\omega (x_i)[S(x_i)-f(x_i){]}^2----(Formula.12)$$

也就是说，只要对一组数据的法方程进行求解，就可以得到唯一一组多项式的系数解。如何求解方程组，将会在后续的博客中给出。

3 最小二乘应用示例

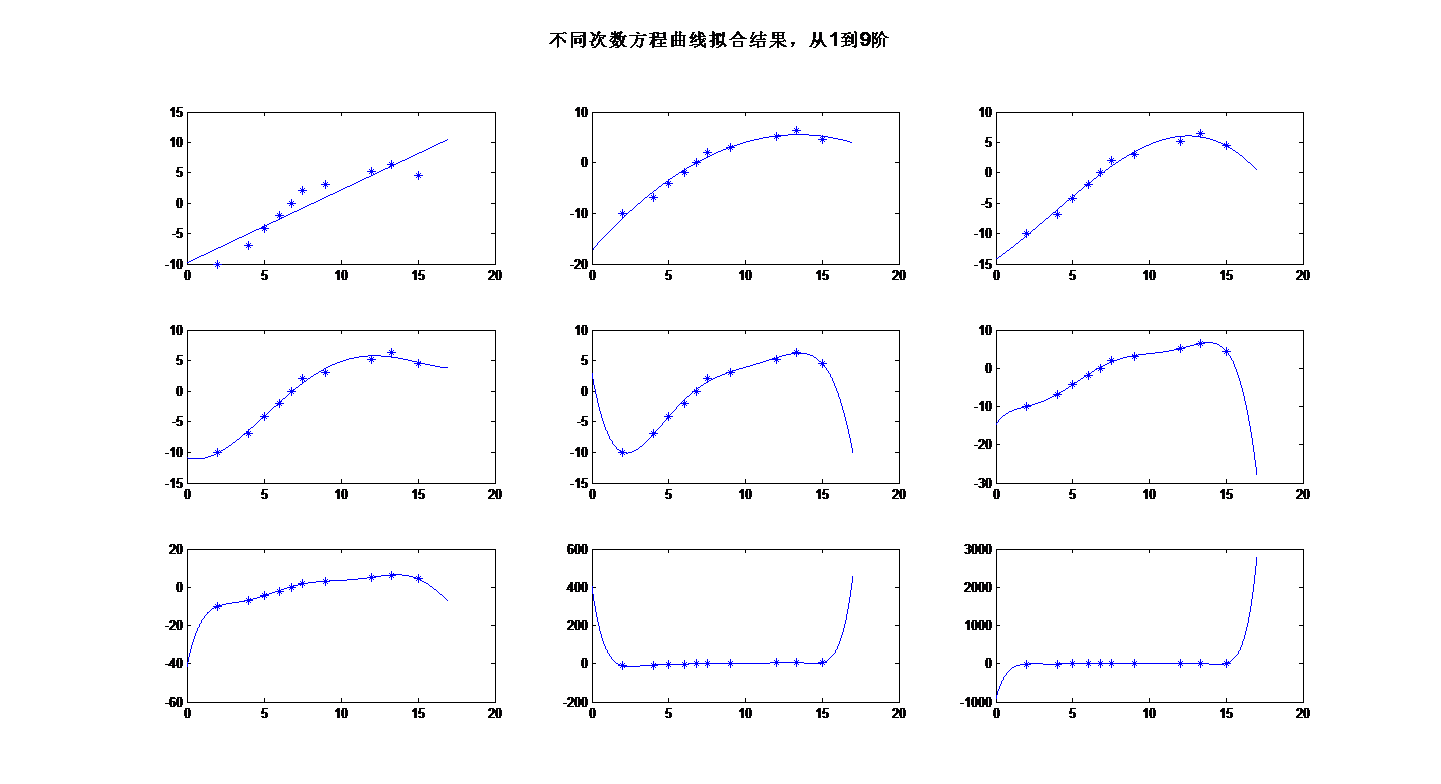
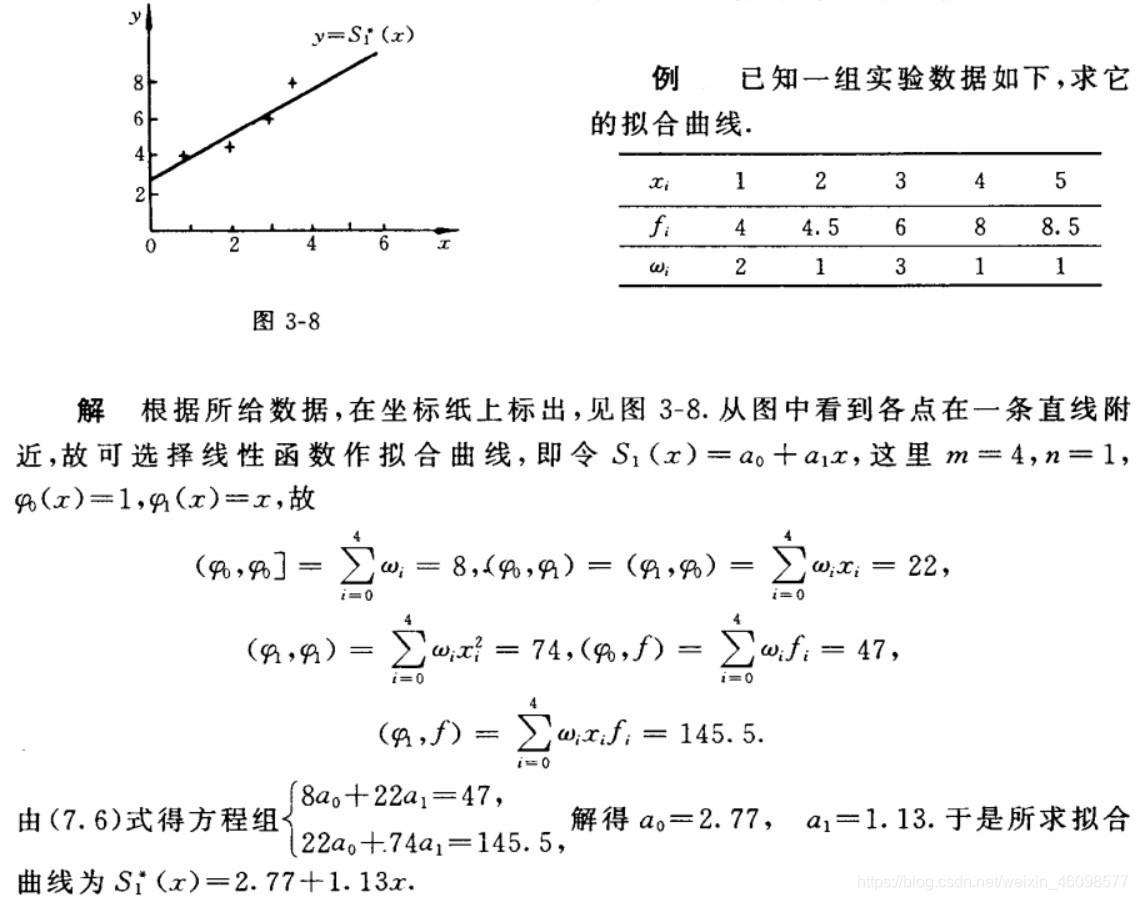
下面通过一个例题进一步理解曲线的最小二乘

4 法方程到底是什么

相信不少人对于法方程 $Ga=d$ 中 $G$ 的元素到底是什么存在疑问，那么 $G$ 中的$\phi$ 到底是什么呢？下面通过分析一阶、二阶、三阶多项式拟合的法方程，帮助大家理解这个问题。

回顾一下 $G$
$$G=\left[\begin{array}{cccc}({\phi }_0,{\phi }_0)& ({\phi }_0,{\phi }_1)& \cdots & ({\phi }_0,{\phi }_n)\\ ({\phi }_1,{\phi }_0)& ({\phi }_1,{\phi }_1)& \cdots & ({\phi }_1,{\phi }_n)\\ ⋮& ⋮& \ddots & ⋮\\ ({\phi }_n,{\phi }_0)& ({\phi }_n,{\phi }_1)& \cdots & ({\phi }_n,{\phi }_n)\end{array}\right]$$

需要明确的一点是：若以 $x$ 为自变量，则 ${\phi }_0(x)=x^0=1，{\phi }_1(x)=x^1，{\phi }_2(x)=x^2，\dots ，{\phi }_n(x)=x^n$.

已知一组数据点 P = { p 1 ( x 1 , y 1 ) , p 2 ( x 2 , y 2 ) , … , p m ( x m , y m ) } P=\{p_1 (x_1,y_1 ),p_2 (x_2,y_2 ),…,p_m (x_m,y_m )\} P={p1​(x1​,y1​),p2​(x2​,y2​),…,pm​(xm​,ym​)}，每个点只观测一次，即 $\omega (x)\equiv 1$. 分别对其进行一阶、二阶、三阶多项式拟合，对应的拟合函数与法方程如下：

拟合阶数	拟合函数	法方程
1	$S(x)=a_0+a_{1}x$	$\left[\begin{array}{ccc}{\sum }_{i=1}^m{x}_i^0& {\sum }_{i=1}^m{x}_i^1& \\ {\sum }_{i=1}^m{x}_i^1& {\sum }_{i=1}^m{x}_i^2& \end{array}\right]$$\left[\begin{array}{c}{a}_0\\ a_1\end{array}\right]$=$\left[\begin{array}{c}{\sum }_{i=1}^m{x}_i^0{y}_i^1\\ {\sum }_{i=1}^m{x}_i^1{y}_i^1\end{array}\right]$ (详细)
1	$S(x)=a_0+a_{1}x$	$\left[\begin{array}{cc}m& \sum x\\ \sum x& \sum x^2\end{array}\right]$ $\left[\begin{array}{c}{a}_0\\ a_1\end{array}\right]$=$\left[\begin{array}{c}\sum y\\ \sum xy\end{array}\right]$
2	$S(x)=a_0+a_{1}x+a_2{x}^2$	$\left[\begin{array}{ccc}m& \sum x& \sum x^2\\ \sum x& \sum x^2& \sum x^3\\ \sum x^2& \sum x^3& \sum x^4\end{array}\right]$ $\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\end{array}\right]$=$\left[\begin{array}{c}\sum y\\ \sum xy\\ \sum x^{2}y\end{array}\right]$
3	$S(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3$	$\left[\begin{array}{cccc}m& \sum x& \sum x^2& \sum x^3\\ \sum x& \sum x^2& \sum x^3& \sum x^4\\ \sum x^2& \sum x^3& \sum x^4& \sum x^5\\ \sum x^3& \sum x^4& \sum x^5& \sum x^6\end{array}\right]$ $\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\\ a_3\end{array}\right]$=$\left[\begin{array}{c}\sum y\\ \sum xy\\ \sum x^{2}y\\ \sum x^{3}y\end{array}\right]$
…	…	…

为了便于理解，首先给出一阶多项式详细的法方程。

对比不同阶数的法方程可以看出，$G$ 中的每个元素以一定规律对自变量的 $k$ 次幂进行求和得到，低阶的法方程是高阶的法方程的一个 “子集”，且矩阵 $G$ 为对称正定矩阵。

相关链接

基于Eigen库的线性方程组/矩阵方程求解(方法汇总)

最小二乘曲线拟合的C++实现

---

参考资料：

《数值分析》李庆扬