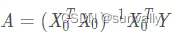说明,本文章的源代码来着于网络,本人已在实际项目中反复使用过,证明没问题。
1.简介
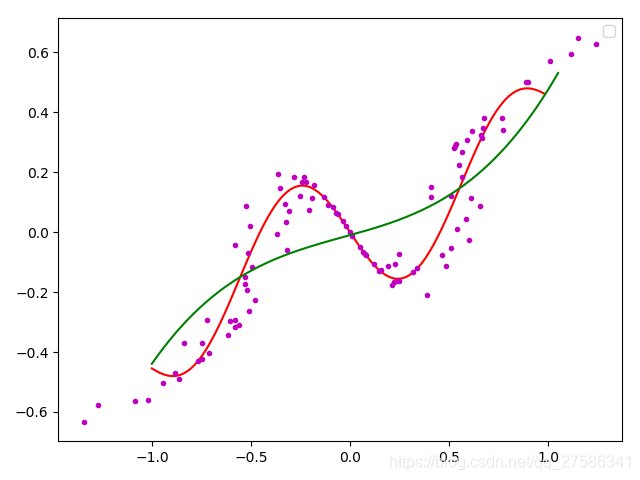
已知曲线上的n个点,可以使用某条曲线去拟合,使得整体上所有的点都逼近曲线,可以使用不同的角度去判断整体逼近,最小二乘法是使用偏差平方和最小的方式。
2.C语言实现
static void gauss_solve(int n,double A[],double x[],double b[]);double *tempx = NULL,*tempy = NULL,*sumxx = NULL,*sumxy = NULL,*ata = NULL;/*==================polyfit(n,x,y,poly_n,a)===================*/
/*=======拟合y=a0+a1*x+a2*x^2+……+apoly_n*x^poly_n========*/
/*=====n是数据个数 xy是数据值 poly_n是多项式的项数======*/
/*===返回a0,a1,a2,……a[poly_n],系数比项数多一(常数项)=====*/
void polyfit(int n,double x[],double y[],int poly_n,double p[])
{int i,j;//double *tempx,*tempy,*sumxx,*sumxy,*ata;#if 0tempx = (double *)calloc(n , sizeof(double));sumxx = (double *)calloc((poly_n*2+1) , sizeof(double));tempy = (double *)calloc(n , sizeof(double));sumxy = (double *)calloc((poly_n+1) , sizeof(double));ata = (double *)calloc( (poly_n+1)*(poly_n+1) , sizeof(double) );
#elsetempx = (double *) mymalloc( SRAMIN ,n*sizeof(double));sumxx = (double *) mymalloc( SRAMIN ,(poly_n*2+1)*sizeof(double));tempy = (double *) mymalloc( SRAMIN ,n*sizeof(double));sumxy = (double *) mymalloc( SRAMIN ,(poly_n+1)*sizeof(double));ata = (double *) mymalloc( SRAMIN ,(poly_n+1)*(poly_n+1)*sizeof(double));
#endiffor (i=0;i<n;i++){tempx[i]=1;tempy[i]=y[i];}for (i=0;i<2*poly_n+1;i++){for (sumxx[i]=0,j=0;j<n;j++){sumxx[i]+=tempx[j];tempx[j]*=x[j];}}for (i=0;i<poly_n+1;i++){for (sumxy[i]=0,j=0;j<n;j++){sumxy[i]+=tempy[j];tempy[j]*=x[j];}}for (i=0;i<poly_n+1;i++){for (j=0;j<poly_n+1;j++){ata[i*(poly_n+1)+j]=sumxx[i+j];}}gauss_solve(poly_n+1,ata,p,sumxy);#if 0free(tempx);free(sumxx);free(tempy);free(sumxy);free(ata);
#else myfree( SRAMIN,tempx); myfree( SRAMIN,sumxx);myfree( SRAMIN,tempy);myfree( SRAMIN,sumxy);myfree( SRAMIN,ata);
#endif
}/*============================================================*/高斯消元法计算得到 n 次多项式的系数n: 系数的个数ata: 线性矩阵sumxy: 线性方程组的Y值p: 返回拟合的结果
/*============================================================*/
static void gauss_solve(int n,double A[],double x[],double b[])
{int i,j,k,r;double max;for (k=0;k<n-1;k++){max=fabs(A[k*n+k]); // find maxmum r=k;for (i=k+1;i<n-1;i++){if (max<fabs(A[i*n+i])){max=fabs(A[i*n+i]);r=i;}}if (r!=k){for (i=0;i<n;i++) //change array:A[k]&A[r]{max=A[k*n+i];A[k*n+i]=A[r*n+i];A[r*n+i]=max;}max=b[k]; //change array:b[k]&b[r]b[k]=b[r];b[r]=max;}for (i=k+1;i<n;i++){for (j=k+1;j<n;j++)A[i*n+j]-=A[i*n+k]*A[k*n+j]/A[k*n+k];b[i]-=A[i*n+k]*b[k]/A[k*n+k];}} for (i=n-1;i>=0;x[i]/=A[i*n+i],i--){for (j=i+1,x[i]=b[i];j<n;j++)x[i]-=A[i*n+j]*x[j];}
}
3 实验验证
使用VC验证:
int main(int argc, char* argv[])
{double P[6];double xx[4] = {27.5,32.5,37.5,42.5};double yy[4] = {1.2,0.8,0.6,0.4};// 拟合 y = p1*x^2 + p2*x + p3 // 特别注意这里是的顺序 !!!polyfit(4, xx, yy, 2, P);printf("y = %f*x^2 + %f*x + %f\r\n\r\n",P[2],P[1],P[0]);return 0;
}输出结果:
![]()
这里我们为了验证准确性,我们使用matlab也拟合一遍,看结果是否一致。
xx = [27.5 32.5 37.5 42.5];
yy = [1.2 0.8 0.6 0.4];
plot(xx,yy);
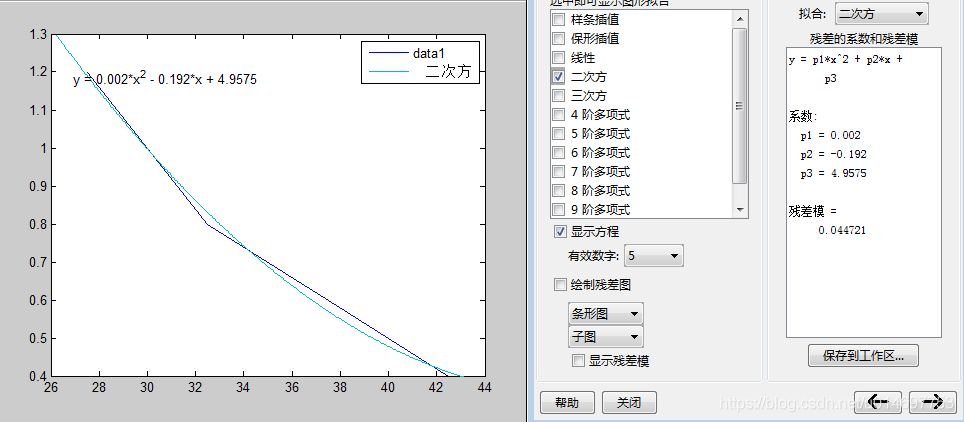
可以看到,最终matlab拟合的曲线和C语言运行拟合的曲线完全一致,另外本人在实际工程中也多次使用验证过没问题的。