线性回归----最小二乘法

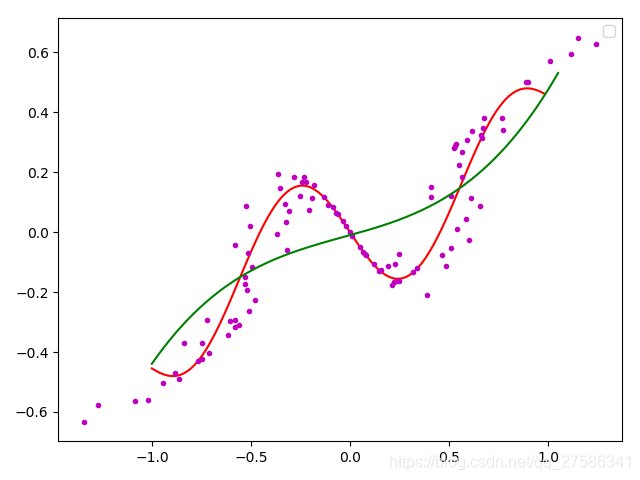
线性回归：就是把离散的数据拟合到一条直线上，获得一个直线方程来近似的描述这些离散的数据

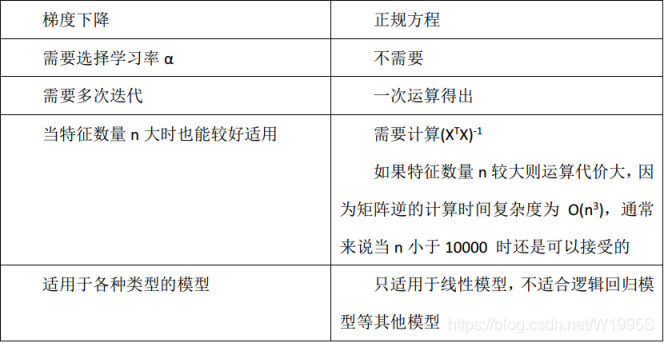
最小二乘法：是用数学公式直接求解线性回归方程的参数的方法。

例：使用美国汽车油耗数据中的排量disp作为X，油耗MPG作为Y。

线性回归：就是把离散的数据拟合到一条直线上，获得一个直线方程来近似的描述这些离散的数据

回归分析的基本原理是归纳与预测信息，也就是说，通过已有的信息（就是已知的数据集）去推测出新的未知的信息。

线性回归使用最佳的拟合直线（也就是回归线）在因变量（Y）和一个或多个自变量（X）之间建立一种关系，如果变量Y与变量X之间的相关关系表现为线性组合，那么绘制的X-Y散点图就会近似的聚集在一条直线附件，对于单自变量的简单线性回归，即一元线性回归，Y是X的线性函数，其线性回归方程是：

Y=cX+b(c表示直线的斜率，b表示截距)

b和c即为该线性函数的参数。当从分散的数据点中拟合处参数c和b之后，对于一个给定的X值，就可以预测出对应的Y值。

如果有多个自变量X1，X2，X3，...，而Y与这些自变量之间也存在着线性相关关系，那么这就是一个多元线性回归问题，它对应的线性回归方程为:

Y=c1X1+c2X2+c3X3+...+cnXn+b

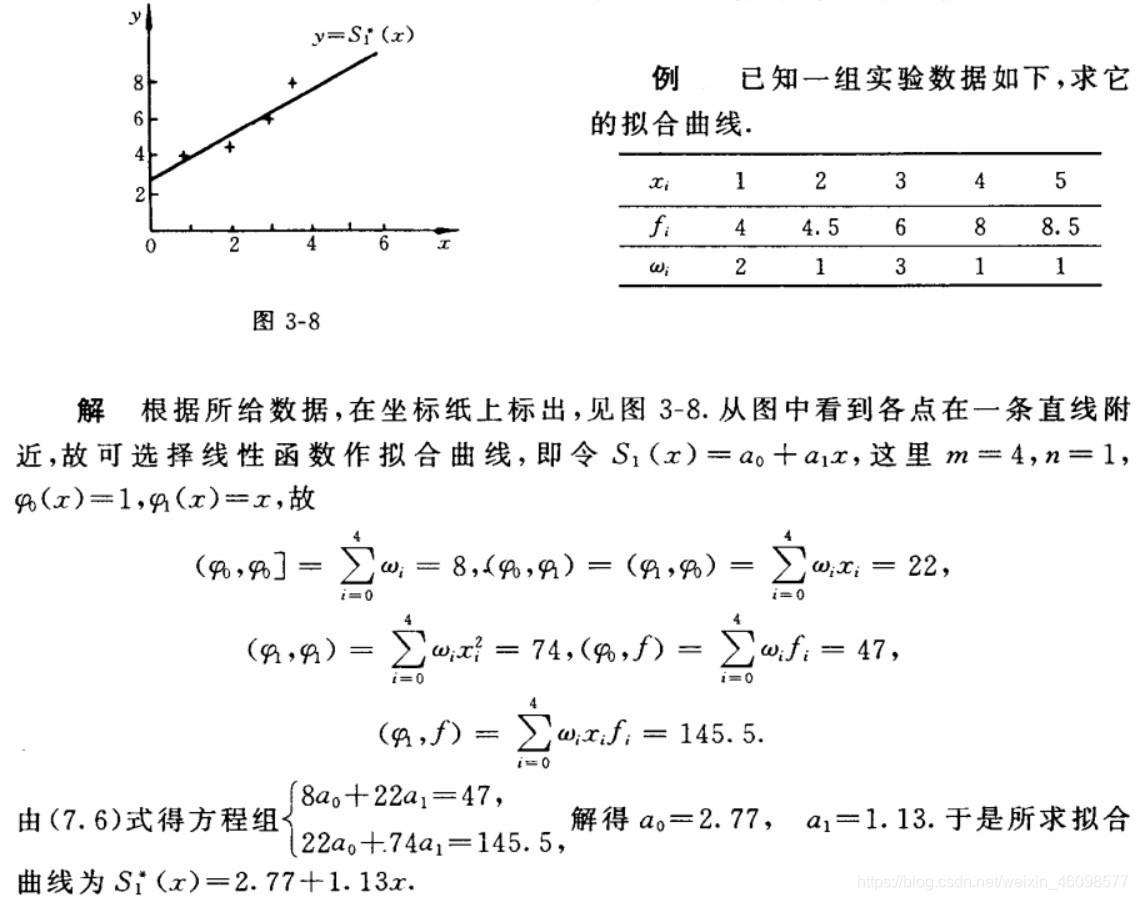
最小二乘法：是用数学公式直接求解线性回归方程的参数的方法。

以一元线性回归方程为例：通过X和Y及相关表示参数c和b。

例：使用美国汽车油耗数据中的排量disp作为X，油耗MPG作为Y。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt#读取文件，以空格分隔各行，原始数据不包括表头
data = pd.read_csv('auto-mpg.csv',sep = '\s+',header = None)#给各列数据设置表头
data.columns = ['MPG','cyl','disp','hp','wt','acc','year','orig','name']df=data[data['hp']!='?']               #排除hp不详的数据
df=df[['disp','MPG']].copy()            #选取要计算的列df['x_xbar']=df.disp-df.disp.mean()    #添加一列X-X.mean()
df['y_ybar']=df.MPG - df.MPG.mean()    #添加一列Y-Y.mean()c = sum(df.x_xbar*df.y_ybar)/sum(df.x_xbar**2)    #计算c
b = df.MPG.mean()-c*df.disp.mean()     #计算bequation = 'MPG={:.4f}*disp+{:.4f}'.format(c,b)   #格式化生成公式
print(equation)def graph(formula,x_range):            #定义一个按公式画线的函数x = np.array(x_range)y = eval(formula)plt.plot(x,y,color = 'r')plt.figure()                           #准备画图
plt.scatter(df.disp,df.MPG)            #画数据点的散点图
graph('x*c+b',range(70,450))           #画y=cx+b的线
plt.text(200,30,equation)              #在图上添加公式
plt.title("MPG vs.displacement")       #设置图的标题
plt.xlabel("disp")                     #设置x轴标签
plt.ylabel("MPG")                      #设置y轴标签
plt.show()                             #显示图形