1、概述

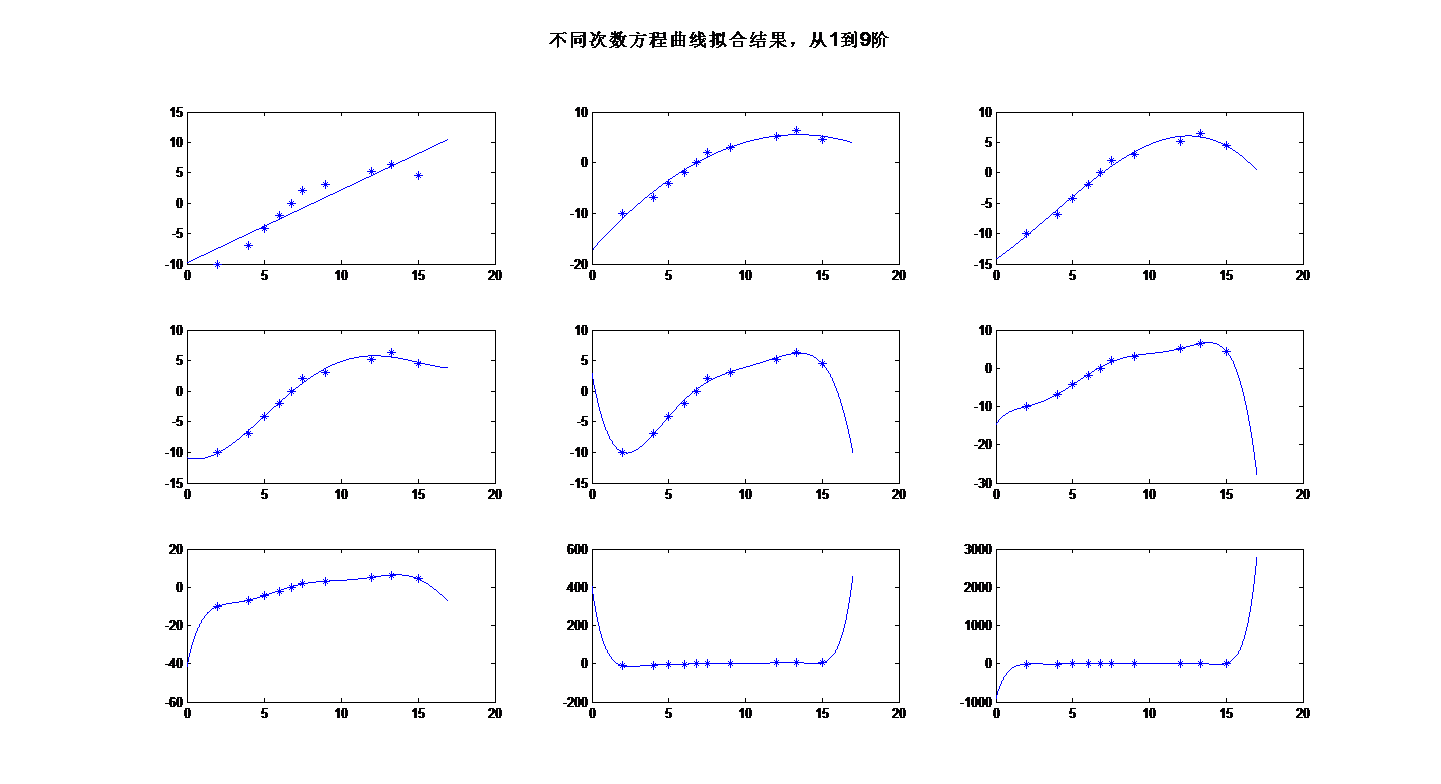
最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差（真实目标对象与拟合目标对象的差）的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

• 最小二乘法还可用于曲线拟合。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。
  选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小
• 最小二乘法也是一种优化方法，求得目标函数的最优值。并且也可以用于曲线拟合，来解决回归问题。回归学习最常用的损失函数是平方损失函数，在此情况下，回归问题可以著名的最小二乘法来解决。

简而言之，最小二乘法同梯度下降类似，都是一种求解无约束最优化问题的常用方法，并且也可以用于曲线拟合，来解决回归问题。

监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。

最小二乘法处理的一般模型表达式如下：

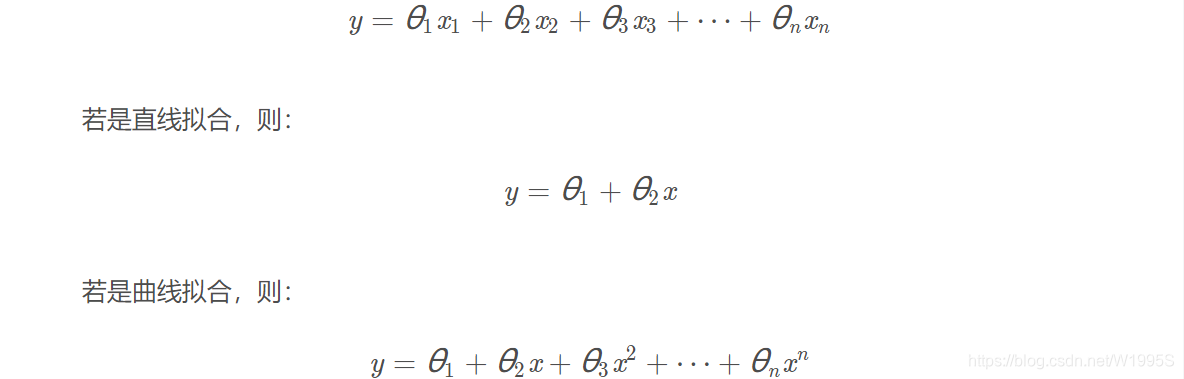
视问题复杂度而定x取几次方。这里可能有人有疑问，最小二乘不是处理线性问题吗？怎么 x^n都出来了？

注意，我们的目的是求取一个非线性方程，但当我们用最小二乘求解时，我们针对的是θ变量，而不是x ，也就是说，机器学习中，这里的x 是输入，是已知量，y 是输出，是预测量， θ 才是我们要学习的变量，所以这还是一个线性问题。

2、定义误差

当然是真实值与拟合值的差

但为啥要平方（2范数）呢？绝对值（1范数）不可以吗？

因为误差是长度，还要取绝对值，计算起来麻烦，就干脆用平方来代表误差。而且平方要比绝对值更能得到最短距离，即使得误差最小化，也就是更能使得拟合函数逼近真实函数。

2.1怎样最小化误差

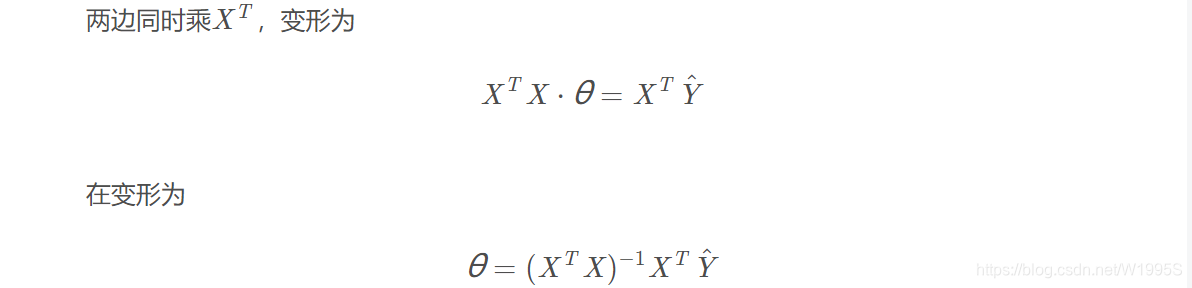
2.2 什么情况下能用这矩阵形式求解

从上面的最后一个式子可以看出，只有当矩阵$X^{T}X$可逆时，该式才成立，最小二乘法则可用，也就是说无法用直接求一阶导数方式，计算出最优解，这时就需要用梯度下降法来迭代逼近最优解。

2.3直线拟合最小二乘法

在这里，最小二乘法就是求解Q 的最小值，因为误差Q 最小，对应θ 值最优；所有我们将上式看成一个Q 关于θ 变量的函数，问题转成一个求极小值问题：

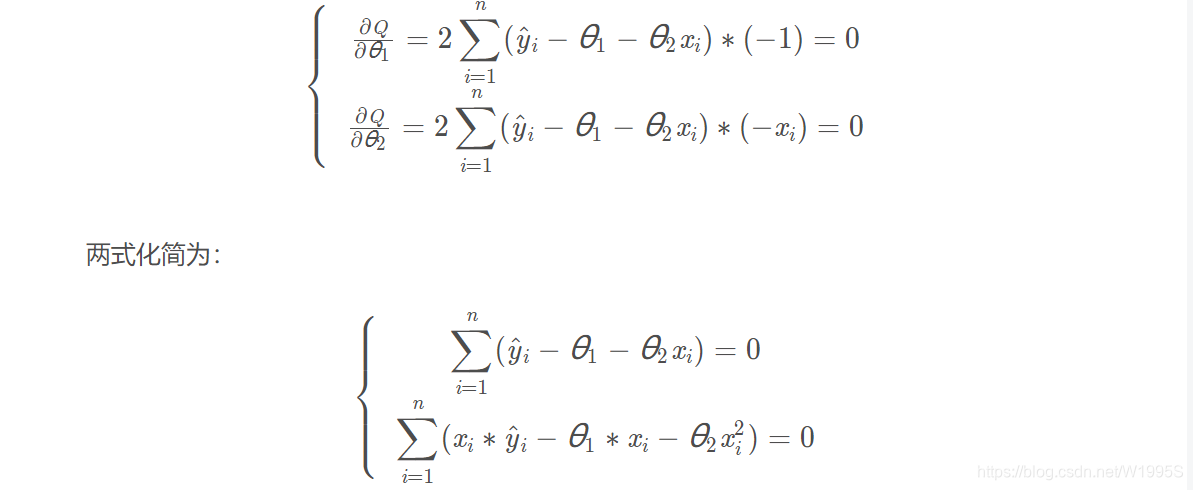
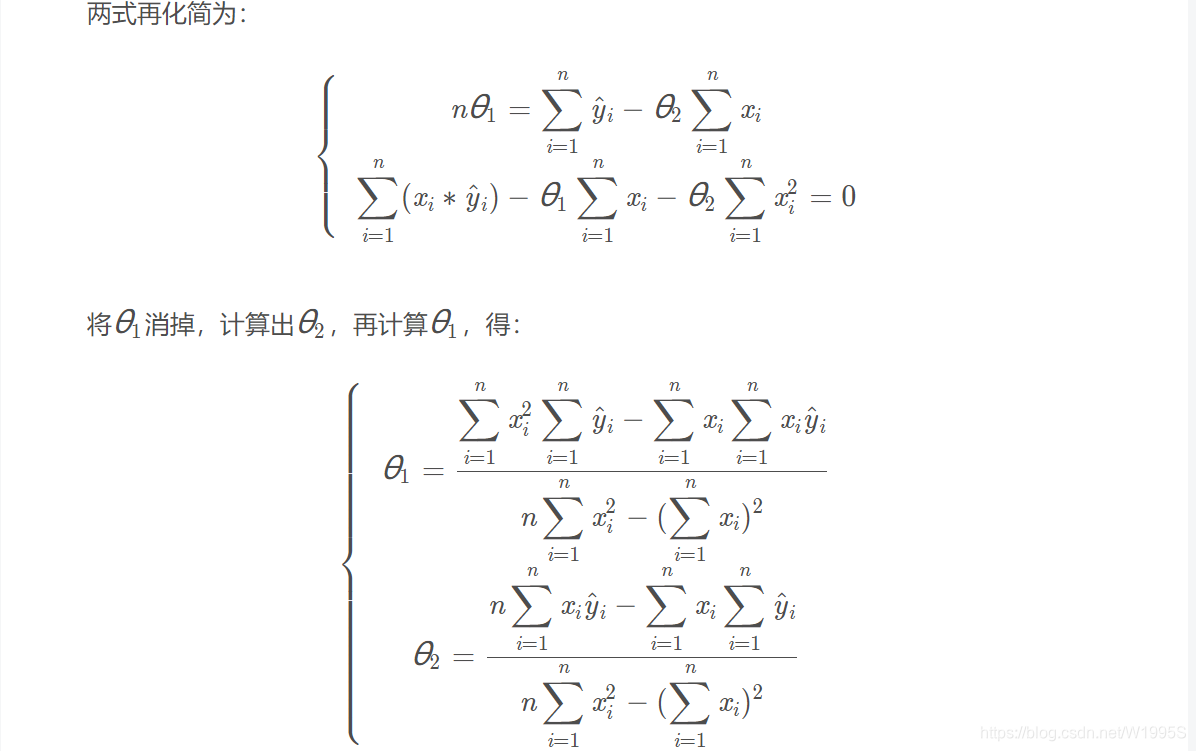
3、和梯度下降法比较

最小二乘法跟梯度下降法都是通过求导来求损失函数的最小值， 首先它们都是机器学习中，计算问题最优解的优化方法，但它们采用的方式不同，前者采用暴力的解方程组方式，直接，简单，粗暴，在条件允许下，求得最优解；而后者采用步进迭代的方式，一步一步的逼近最优解。实际应用中，大多问题是不能直接解方程求得最优解的，所以梯度下降法应用广泛。

最小二乘法和梯度下降法在线性回归问题中的目标函数是一样的(或者说本质相同)，都是通过最小化均方误差来构建拟合曲线。

二者的不同点可见下图(正规方程就是最小二乘法)：

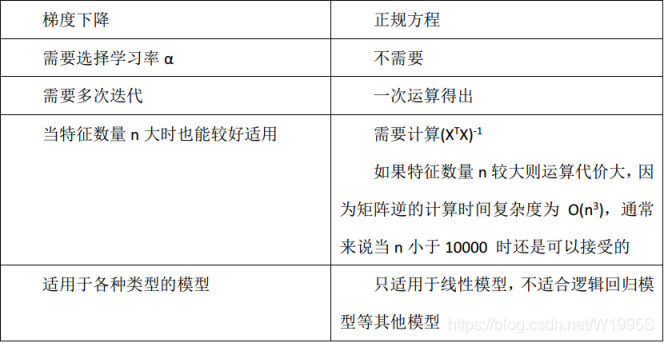
需要注意的一点是最小二乘法只适用于线性模型(这里一般指线性回归)；而梯度下降适用性极强，一般而言，只要是凸函数，都可以通过梯度下降法得到全局最优值(对于非凸函数，能够得到局部最优解)。

梯度下降法只要保证目标函数存在一阶连续偏导，就可以使用。

4、最小二乘法与正态分布