最小二乘法入门（Matlab直线和曲线拟合）

参考博客：https://blog.csdn.net/wokaowokaowokao12345/article/details/72850143

多的就不多说了，持续脱发中！！！

最小二乘法历史起源之类的：https://baike.baidu.com/item/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98%E6%B3%95/2522346?fr=aladdin

WiKi上说的：“"Least squares approximation" redirects here. It is not to be confused with Least-squares function approximation.”

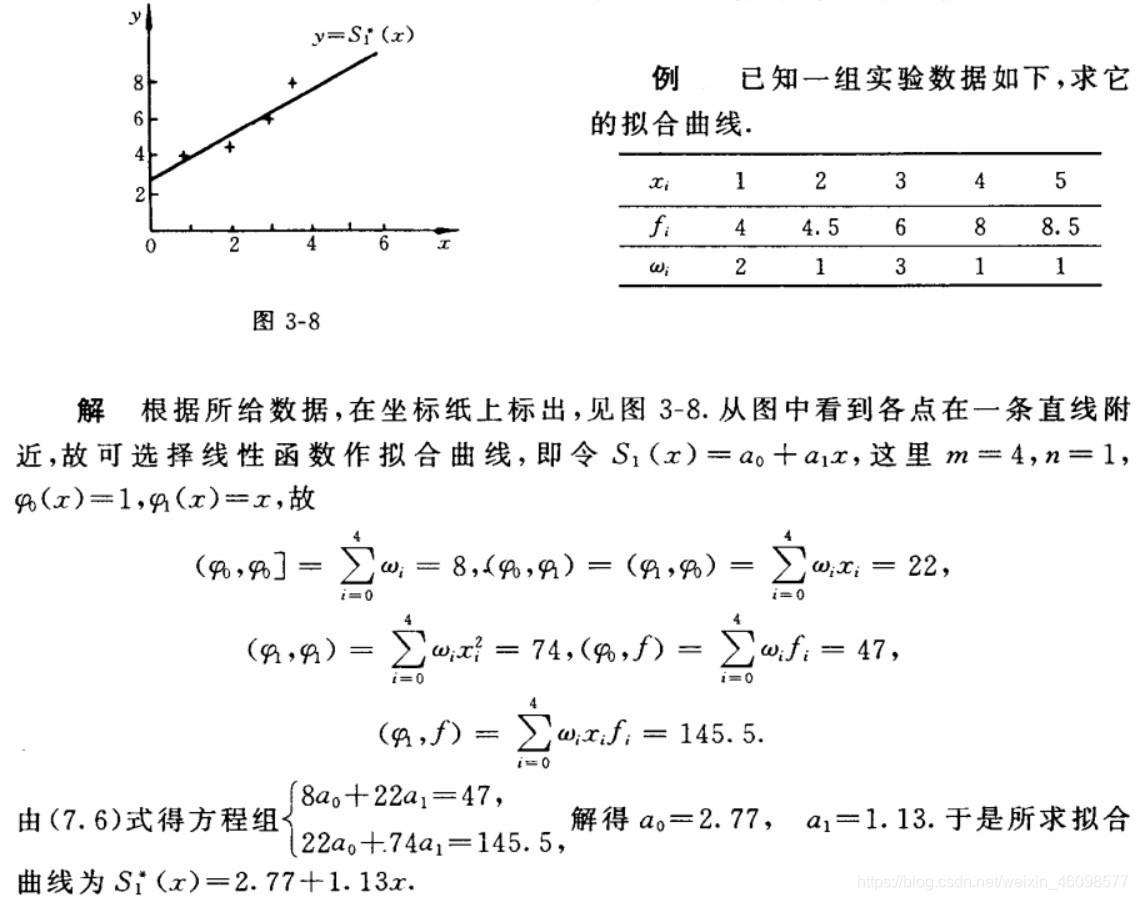
最小二乘法做线性规划的理论好像高中就学了。最小二乘法做直线拟合，实际上就是现在给定了 n 个序列 xi ，而在 xi 下有对应的 yi ，这样也就组成了 n 个（x,y）这样的坐标点。最小二乘法就是要找到一条直线 L ，让这 n 个点与直线 L 的距离（残差，不是点到直线的垂线段距离）平方和最小。不知道叙述的准不准确，大概就是这样一个思想。

根据最小二乘原理（参考博客）：

采用斜截式描述的直线方程： $y=kx+b$ ,这种直线不适用于与y轴平行的直线。假设测得的数据对共 $n>2$ 组， $(x_{_{_{1}}},y_{1}),(x_{_{_{2}}},y_{2}),(x_{_{_{3}}},y_{3}),...(x_{_{_{n}}},y_{n}),$ $n>2$ 也就是说为了求解这个直线方程实际上只需要两个数据对，也就是两点确定一条直线，但是这样的直线对于实际的测量是不准确的，当 n>2 的时候，在理论上求解则因为条件数超出了方程未知数，因此是无解的，所以叫做超定方程。由于真值（理论值）是（ $y=kx_{i}+b$ ）,则将数据对代入，残差即为 $y_{i}-y=y_{i}-kx_{i}-b$ ，由最小二乘方程：

$minf=\sum_{i=1}^{n}(y_{i}-kx_{i}-b)^{2}$

其实这里应该证明 $f$ 是否存在最小值，根据方程可以看出，对于单变量，这是一个开口向上的抛物线，简单的证明就在这里说了。大家都知道为了求解方程的最小值，一种方法就是对方程求导，导数为 0 的地方就是极值，对于抛物线来说也是最值。这里变量有两个 $k,b$ ，通过求偏导得出下述方程：

真的不是我懒得打公式，CSDN公式编辑器抽风了，求和打不出来！！！！！这里的截图也是前面参考博客的。将上式展开得到：

实际上，上述计算 k , b 的方程就是最小二乘线性拟合精华了。

依据上述模型，自己写了点Matlab代码供大家参考：

function [k,t] = user_define(ind,dp)
if length(ind)~= length(dp)disp('数组长度不等，请检查！');       % 要求 x,y 一一对应
end
% 最小二乘法的系数设置，参考数学模型a = ind*ind';b = sum(ind);c = ind*dp';d = sum(dp);
% 求解斜率k
k = (length(ind).*c-b*d)./(length(ind).*a-b*b);
% 求解截距t
t = (a.*d-c.*b)/(a*length(ind)-b.*b);
end

这个函数实际上就是对模型写的，当然还可以调用 Matlab 内置的函数 polyfit ：

% 设将要拟合的直线为 y = 2x+3，该直线为理想情况
% 现对直线上 x>0 随机取点20个，分别对应x[20] y[20]
clear
clc
%y = 2*x +3;
a = [1,5];  % 直线上的点（1，5）
b = [5,13];     % 直线上的点（5，13）
% 初始化参数，以提升计算效率
% 否则会提示警告：“变量似乎会随着迭代次数改变而变化，请预分配内存，以提高运行速度”
% t = zero(1,20);
% p = zero(1,20);
t(1) = 0;
p(1) = 0;
% 生成的t(i)和p（i）为直线上的随机点
for i = 1:20t(i) = rand(1,1)*5;p(i) = 2*t(i)+3;
end% 对采集到的离散的t(i),p(i)加入wng(1,size(t),1)的高斯白噪声，生成的序列作为含误差的测量序列
t = sort(t);
p = sort(p);
% 采用带绝对值的高斯白噪声
% t_g = t + abs(wgn(1,20,0));
% p_g = p + abs(wgn(1,20,0));
% 使用（-1，1）的随机数来给测试序列添加噪声
% t_g = t + (rand(1,20)*2-1);
% p_g = p + (rand(1,20)*2-1);
% 高斯白噪声
t_g = t + wgn(1,20,0);
p_g = p + wgn(1,20,0);
% 最小二乘法对 t_g 和 p_g 拟合
% 这里才开始最小二乘法
% 首先使用Matlab内置的最小二乘函数 polyfit 进行多项式拟合，具体自己查help
% 注：type函数可帮助查看源代码
line1 = polyfit(t_g,p_g,1);
t_g2 = 1:0.1:5;
p_g2 = polyval(line1,t_g2);
plot(t_g,p_g,'o',t_g2,p_g2);
legend('拟合的曲线');
hold on
ideal_line = 2*t_g2+3;
plot(t_g2,ideal_line,'b');
legend('样本点','拟合的曲线','原直线');