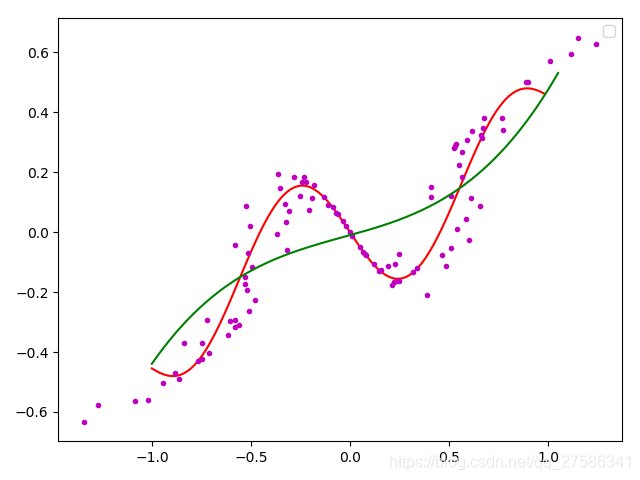
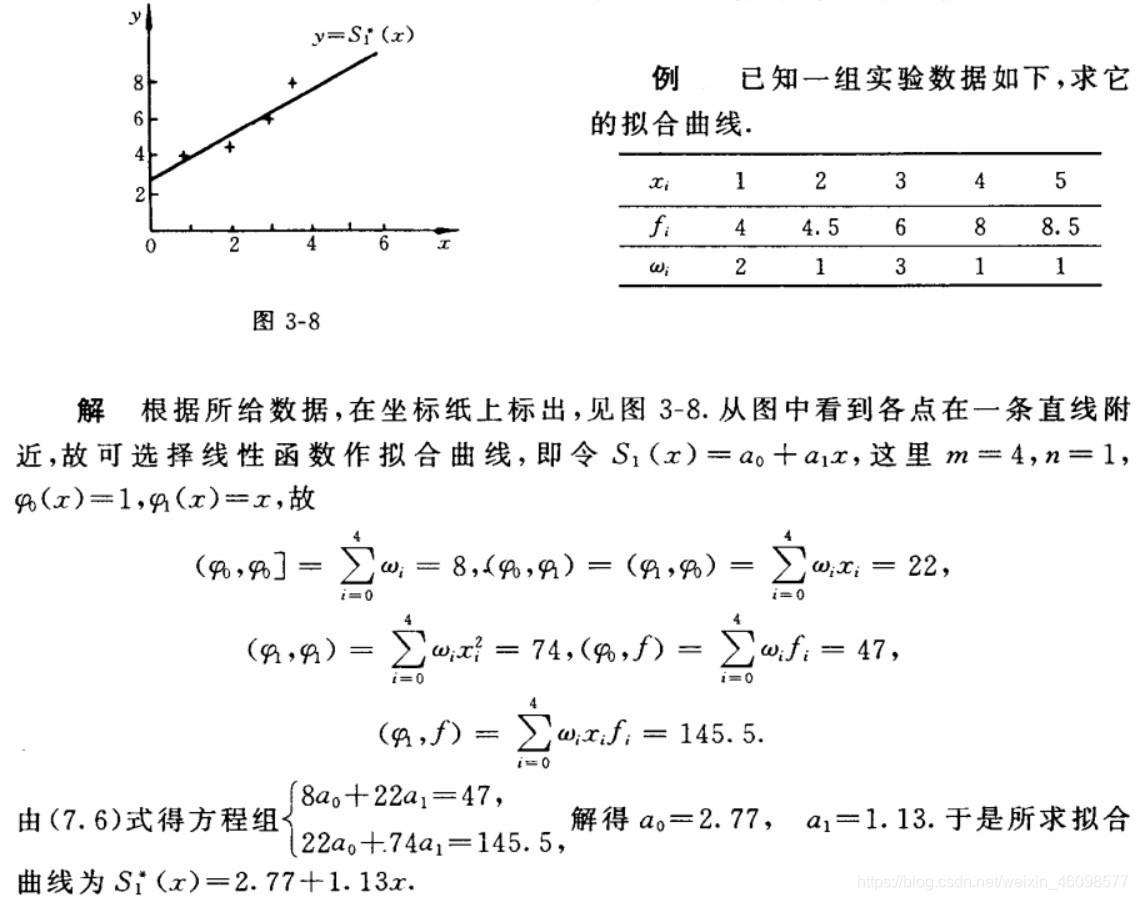
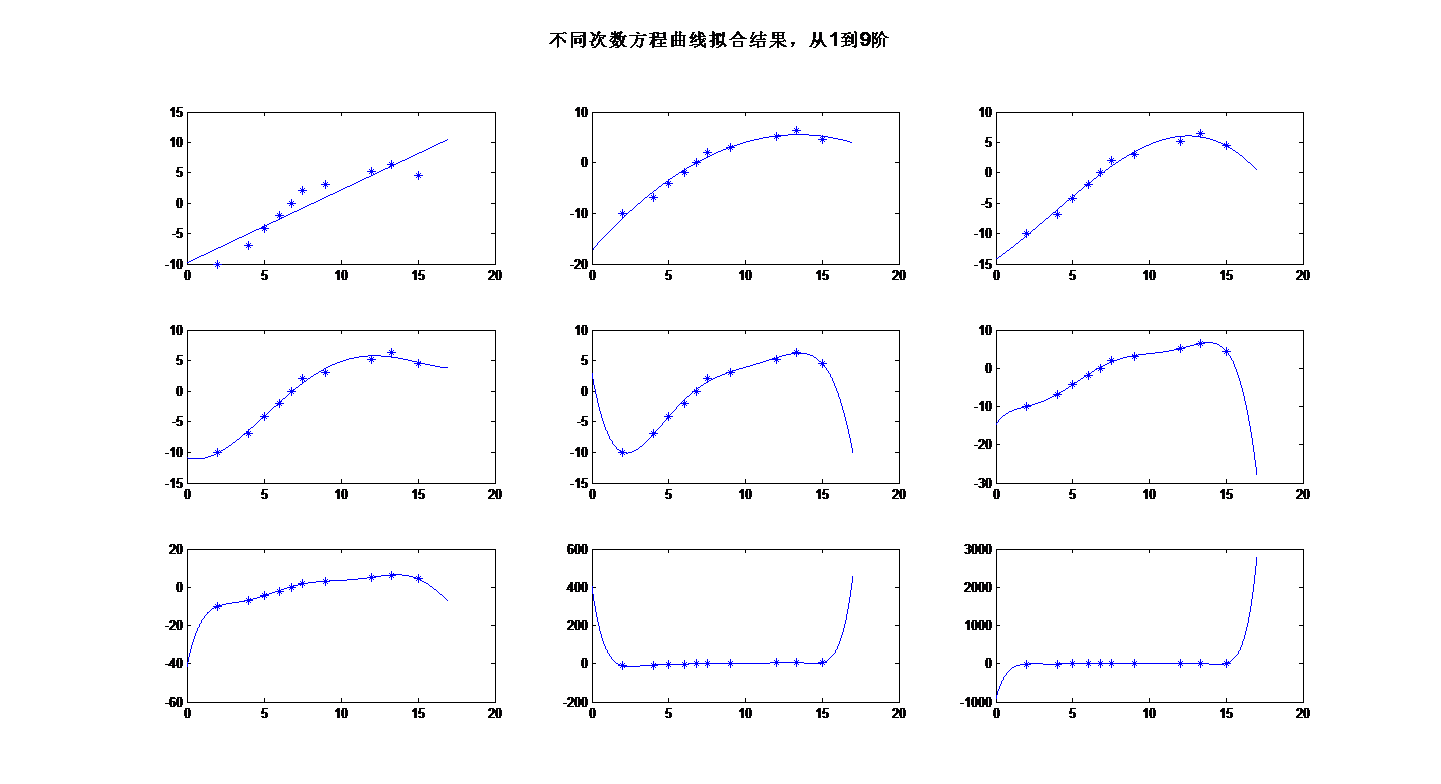
最近由于项目要求，应用了最小二乘法线性拟合和2次曲线拟合算法，现总结如下：
最小二乘法线性拟合应用已有的采样时间点，再现这些点所描述的线性变化，即求出一个线性方程y=ax+b(这个算法的主要问题也就是如何用给定的数据求线性方程系数a和b)
//最小二乘法线性拟合,线性方程求系数,Xval时间数据，Yval每个时间点上的值数据，n数据的个数，Aval线性方程系数a,Bval线性方程系数b
BOOL DlgDataAnalyse::TwoCurveCompose(double *Xval,double *Yval,long n,double *Aval,double *Bval)
{
double mX,mY,mXX,mXY;
mX=mY=mXX=mXY=0;
for (int i=0;i<n;i++)
{
mX+=Xval[i];
mY+=Yval[i];
mXX+=Xval[i]*Xval[i];
mXY+=Xval[i]*Yval[i];
}
if(mX*mX-mXX*n==0)return FALSE;
*Aval=(mY*mX-mXY*n)/(mX*mX-mXX*n);
*Bval=(mY-mX*(*Aval))/n;
return TRUE;
}
最小二乘法2次曲线拟合应用已有的采样时间点，再现这些点所描述的2次曲线的变化，即求出一个二次曲线方程y=ax2+bx+c (这个算法的主要问题也就是如何用给定的数据求方程系数abc)
今天使用拟合的最小二乘法，求出了给定的一组坐标系上的点对最接近的直线的。
其具体理论如下：
在科学实验数据处理中，往往要根据一组给定的实验数据
，求出自变量x与因变量y的函数关系
，这是
为待定参数，由于观测数据总有误差，且待定参数ai的数量比给定数据点的数量少(即n＜m)，因此它不同于插值问题.这类问题不要求
通过点
，而只要求在给定点
上的误差
的平方和
最小.当
时，即
(5.8.1)
这里
是线性无关的函数族，假定在
上给出一组数据
，
以及对应的一组权
，这里
为权系数，要求
使
最小，其中
(5.8.2)
这就是最小二乘逼近，得到的拟合曲线为y=s(x)，这种方法称为曲线拟合的最小二乘法.
(5.8.2)中实际上是关于
的多元函数，求I的最小值就是求多元函数I的极值，由极值必要条件，可得
(5.8.3)
根据内积定义(见第三章)引入相应带权内积记号
(5.8.4)
则(5.8.3)可改写为
这是关于参数的线性方程组，用矩阵表示为
(5.8.5)
(5.8.5)称为法方程.当
线性无关，且在点集
上至多只有n个不同零点，则称
在X上满足Haar条件，此时(5.8.5)的解存在唯一(证明见［3］).记(5.8.5)的解为
从而得到最小二乘拟合曲线
(5.8.6)
可以证明对
，有
故(5.8.6)得到的
即为所求的最小二乘解.它的平方误差为
(5.8.7)
均方误差为
在最小二乘逼近中，若取
，则
，表示为
(5.8.8)
此时关于系数
的法方程(5.8.5)是病态方程，通常当n≥3时都不直接取
作为基。
//最小二乘法二次曲线拟合算法,Xval时间数据，Yval每个时间点上的值数据，M代表几次曲线(如：2次的话就是3)，N数据的个数，A二次曲线方程的系数(A[2]代表a,A[1]代表b,A[0]代表c)
BOOL DlgDataAnalyse::CalculateCurveParameter(double *Xval,double *Yval,long M,long N,double *A)
{
//X,Y -- X,Y两轴的坐标
//M -- 次数，表示几次曲线
//N -- 采样数目
//A -- 结果参数
register long i,j,k;
double Z,D1,D2,C,P,G,Q;
CDoubleArray B,T,S;
B.SetSize(N);
T.SetSize(N);
S.SetSize(N);
if(M>N)M=N;
for(i=0;i<M;i++)
A[i]=0;
Z=0;
B[0]=1;
D1=N;
P=0;
C=0;
for(i=0;i<N;i++)
{
P=P+Xval[i]-Z;
C=C+Yval[i];
}
C=C/D1;
P=P/D1;
A[0]=C*B[0];
if(M>1)
{
T[1]=1;
T[0]=-P;
D2=0;
C=0;
G=0;
for(i=0;i<N;i++)
{
Q=Xval[i]-Z-P;
D2=D2+Q*Q;
C=Yval[i]*Q+C;
G=(Xval[i]-Z)*Q*Q+G;
}
C=C/D2;
P=G/D2;
Q=D2/D1;
D1=D2;
A[1]=C*T[1];
A[0]=C*T[0]+A[0];
}
for(j=2;j<M;j++)
{
S[j]=T[j-1];
S[j-1]=-P*T[j-1]+T[j-2];
if(j>=3)
{
for(k=j-2;k>=1;k--)
S[k]=-P*T[k]+T[k-1]-Q*B[k];
}
S[0]=-P*T[0]-Q*B[0];
D2=0;
C=0;
G=0;
for(i=0;i<N;i++)
{
Q=S[j];
for(k=j-1;k>=0;k--)
Q=Q*(Xval[i]-Z)+S[k];
D2=D2+Q*Q;
C=Yval[i]*Q+C;
G=(Xval[i]-Z)*Q*Q+G;
}
C=C/D2;
P=G/D2;
Q=D2/D1;
D1=D2;
A[j]=C*S[j];
T[j]=S[j];
for(k=j-1;k>=0;k--)
{
A[k]=C*S[k]+A[k];
B[k]=T[k];
T[k]=S[k];
}
}
return TRUE;
}
