最小二乘法多项式曲线拟合及其python实现
- 多项式曲线拟合问题描述
- 最小二乘法
- 针对overfitting,加入正则项
- python实现
- 运行结果
多项式曲线拟合问题描述
 问题描述:给定一些数据点,用一个多项式尽可能好的拟合出这些点排布的轨迹,并给出解析解
问题描述:给定一些数据点,用一个多项式尽可能好的拟合出这些点排布的轨迹,并给出解析解
判断拟合的好坏常用的误差衡量方法是均方根误差,要求均方根误差先要求平方和误差:
 然后计算均方根误差:
然后计算均方根误差:
 多项式拟合问题本质是一个优化问题,目标函数是使RMS误差最小。
多项式拟合问题本质是一个优化问题,目标函数是使RMS误差最小。
本文关注于最小二乘法优化。
最小二乘法
 最小二乘法推导:RMS误差与E(W)成正比,E(W)最优等价于RMS最优
最小二乘法推导:RMS误差与E(W)成正比,E(W)最优等价于RMS最优
E(W):
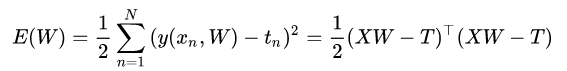
对E(W)求导:

令导数=0:
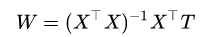
通过给定X和T,可以直接求得W,W就是多项式拟合中的系数矩阵。
针对overfitting,加入正则项
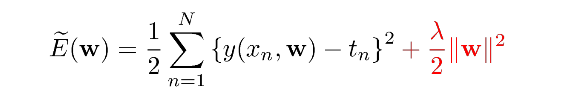 求导:
求导:
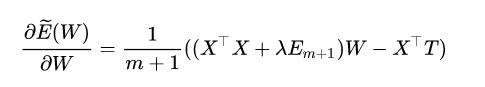
求出W:
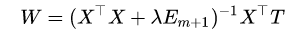
python实现
import numpy as np
import math
import matplotlib.pyplot as plt
SAMPLE_NUM=200#要生成的sample个数
M=9#多项式阶数#产生带有高斯噪声的信号
mid, sigma = 0, 0.3 # 设置均值和方差
noise = np.random.normal(mid, sigma, SAMPLE_NUM).reshape(SAMPLE_NUM,1) #生成SAMPLE_NUM个数据#产生SAMPLE_NUM个序号(范围是2pi)
x = np.arange(0, SAMPLE_NUM).reshape(SAMPLE_NUM,1)/(SAMPLE_NUM-1)*(2*math.pi)#generate y and y_noise, and both y's and y_noise's shape is (SAMPLE_NUM*1)
y=np.sin(x)
y_noise=np.sin(x)+noise#绿色曲线显示x - y,散点显示x - y_noise
plt.title("")
plt.plot(x,y,'g',lw=4.0)
plt.plot(x,y_noise,'bo')#generate Matrix X which has M order
X=x
for i in range(2,M+1):X = np.column_stack((X, pow(x,i)))#add 1 on the first column of X, now X's shape is (SAMPLE_NUM*(M+1))
X = np.insert(X,0,[1],1)
#print(X)#calculate W, W's shape is ((M+1)*1)#
#W=np.linalg.inv((X.T.dot(X))).dot(X.T).dot(y_noise)#have no regularization
W=np.linalg.inv((X.T.dot(X))+np.exp(-8) * np.eye(M+1)).dot(X.T).dot(y_noise)#introduce regularization
y_estimate=X.dot(W)#红色曲线显示x - y_estimate
plt.plot(x,y_estimate,'r',lw=4.0)
plt.show()
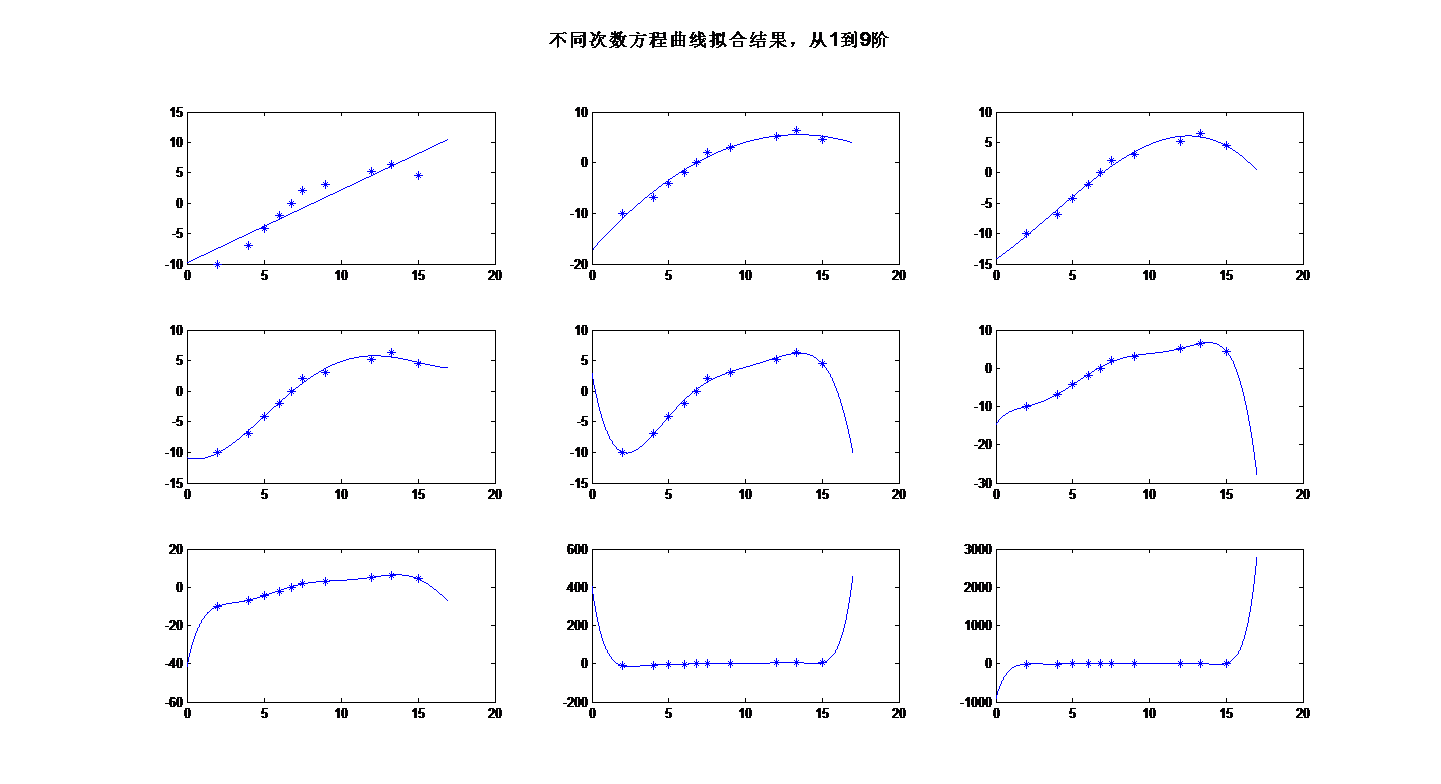
运行结果
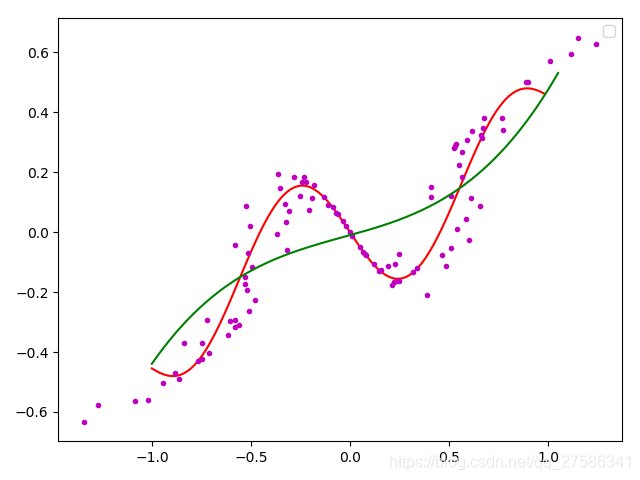
绿色曲线 x-y
蓝色散点 x-y_noise
红色曲线 x-y_eatimate
-
sample number=10,3th

-
sample number=10,9th

-
sample number=15,9th

-
sample number=100,9th

-
sample number=10,9th 加入正则项

加入正则项会有效缓解overfitting问题。