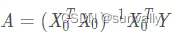1.倒置字符串

倒置字符串

要将每一个单词逆序输出，首先可以将整个字符串内容都逆序输出，然后再将字符串中的每一个单词再进行逆序。

例如：逆序 i like beijing.

先逆序成：.gnijieb ekil i

再将每个单词逆序： beijing. like i

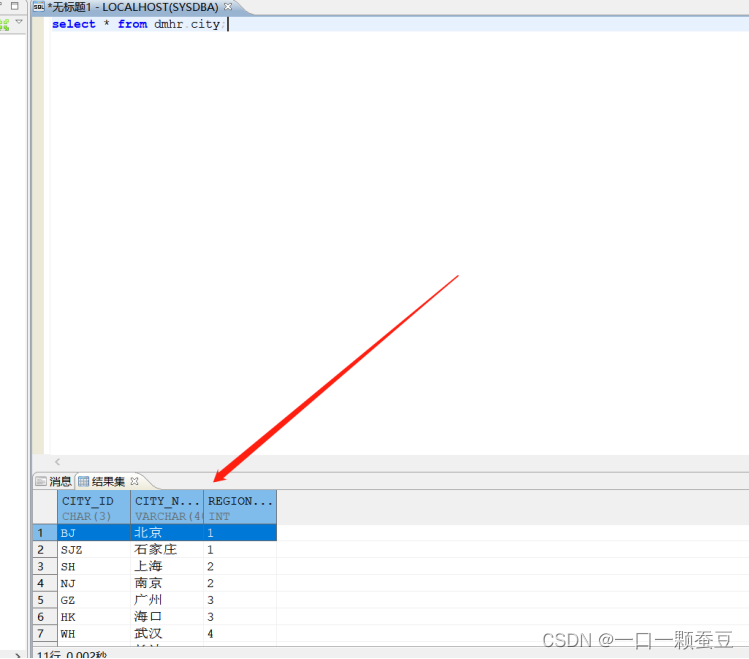
1.1 字符串的读取

先创建一个字符数组：char arr[101];（因为题目中的字符串长度最大是100，这里多出一个用于存放’\0’）；

首先要从键盘读取字符串，有下列方式;

• fgets(arr,100,stdin);，100是指最大的读取个数。
• 

• while ((arr[i++] = getchar() )!= '\n');
• gets(arr);

这里要特别注意 while ((arr[i++] = getchar() )!= '\n');这种方式，这种方式读取的字符串编译器并不会在其后面自动追加一个'\0'，不信请看

当我们手动添加 '\0'之后：

1.2 思路

先将整个字符串逆序，再将每个单词逆序。

【先逆序整个字符串】

void reverseall(char* arr, char* end)
{char tmp = *arr;while (arr < end){tmp = *arr;*arr = *end;*end = tmp;arr++;end--;}
}

将字符数组的数组名和该数组的最后一个位置传递给该函数。当 arr和 end相遇时说明整个字符串逆序完成。

数组的最后一个元素的位置的计算方法： char* end = arr + strlen(arr) - 1;

【逆序每个单词】

cvoid reversepart(char* arr, char* end)
{char* start = arr;char* cur = arr;while (*cur){while ((*cur != ' ') && (*cur != '\0')){cur++;}reverseall(start, cur - 1);start = cur + 1;if (*cur != '\0')//至关重要！！不为\0才++cur++;}
}

将逆序之后的数组的数组名和数组的最后一个位置传递给该函数。

创建两个指针变量 cur和 start，start用于记录每个单词的起始位置，cur用于寻找 start指向的单词的最后一个字母。start和 cur都从数组的第一个字符开始，因为单词与单词时间是以一个空格隔开的 ，所以 cur向后移动，直到遇到了空格就停止，start保持不动，此时将 start和 cur-1（这里一定要是cur-1）传递给reversall函数完成该单词的逆置。接着，将cur+1 赋值给start， start就又指向了下一个单词的首字母。cur指向他的后面的一个字母，又进行类似的操作。

注意：这里外层循环一定要判断 cur指向的是否为 '\0'，若为 '\0'则说明该字符串已经全部逆置完成。内层循环 cur也要满足两个条件：1. 不为空格 2. cur指向的不是 ’\0'。当内层while循环跳出时，需要通过if语句进行判断cur。

总体实现：

void reverseall(char* arr, char* end)
{char tmp = *arr;while (arr < end){tmp = *arr;*arr = *end;*end = tmp;arr++;end--;}
}
void reversepart(char* arr, char* end)
{char* start = arr;char* cur = arr;while (*cur){while ((*cur != ' ') && (*cur != '\0')){cur++;}reverseall(start, cur - 1);start = cur + 1;if (*cur != '\0')cur++;}
}
int main() {char arr[101] = { 0 };gets(arr);char* end = arr + strlen(arr) - 1;reverseall(arr, end);reversepart(arr, end);printf("%s", arr);return 0;
}

2.最小公倍数

最小公倍数

2.1 思路

【思路一】：

这两个数假设为a和b，他们相乘得到的数ret一定能将这两个数整除，但是ret是不是最小公倍数还不一定，所以可以将a和b相乘的结果c进行减减操作，假若也能得到能整除a和b的数，将c赋值给ret，如此往复，直到c不小于a和b中的最大值。但是这样做会超时，时间复杂度太高。

#include<stdio.h>
int main()
{int a = 0;int b = 0;scanf("%d %d", &a, &b);int c = a * b;int ret = c;int max = a > b ? a : b;while (c >= max){if (c % a == 0 && c % b == 0)ret = c;c--;}printf("%d\n", ret);
}

【思路二】

公式法：最小公倍数=a和b的乘积/a和b的最大公约数。

#include<stdio.h>
int getcf(int a, int b)//辗转相除法求最大公约数。
{int k = 1;while (k!=0){k = a % b;a = b;b = k;}return a;
}
int main()
{int a = 0;int b = 0;scanf("%d %d", &a, &b);int c = getcf(a,b);int ret = a * b / c;printf("%d ", ret);return 0;
}

【思路三】

假设这两个数是5和7，他们的最小公倍数是35。通过观察发下，35不仅能整除5，也能整除7。那么35是怎么得到的呢？举个例子：先从5开始，用5/7，无法整除，让5*2=10，用10/7，无法整除，让5*3=15，用15/7，无法整除……直到让5*7=35，再让35/7，可以整除。大概思路就是让其中一个数a乘以一个从一开始逐步递增的数i，得到的结果假若能整除b，那么此时的a*i就是要求的最小公倍数。

#include <stdio.h>int main() {long long n =0 ;long long m = 0;scanf("%lld %lld",&m,&n);int i =1;while(i*m%n){i++;}printf("%lld",i*m);return 0;
}