一元多项式计算器（C语言实现）

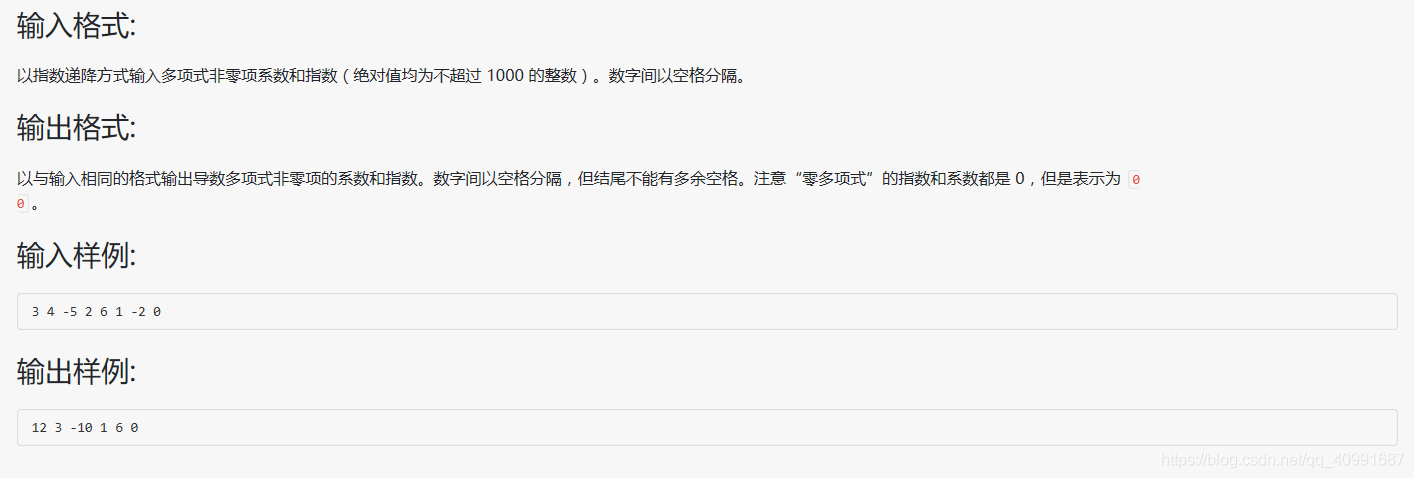
 一、实验要求

 二、代码实现

以下C语言代码实现了多项式的加减法、乘法、求导和顶点求值的功能。

（水平有限，代码存在不规范之处）

编程环境：Window11 + Visual Studio

#define _CRT_SECURE_NO_WARNINGS 1
# include <stdio.h>
# include <stdlib.h>
# include <malloc.h>
# include <math.h>
# define Error -1
# define OK 1//一个节点记录多项式中的一项
typedef struct Polynode
{float coef; //系数int exp;    //指数struct Polynode* next;
}Polynode, * Polypointer;void Menu(Polypointer a, Polypointer b);
Polypointer InitialNode(void);
int CreatePolynomial(Polypointer a, char* filename);
void PrintPoly(Polypointer a);
Polypointer CopyPoly(Polypointer a);
Polynode* AttachNode(float ceof, int e, Polynode* pre);
void AddPoly(Polypointer a, Polypointer b, Polypointer c);
void MinusPoly(Polypointer a, Polypointer b, Polypointer c);
void MultiPoly(Polypointer a, Polypointer b, Polypointer c);
void MultiPoly_2(Polypointer a, Polypointer b, Polypointer c);
Polypointer DiffPoly(Polypointer a, int k);
double GetValue(Polypointer a, double x);
int Write(Polypointer a, char* outfile);
void ClearList(Polypointer a);
//int ReadFromOnefile(Polypointer a,Polypointer b,char*file);int main(void)
{Polypointer a = InitialNode();Polypointer b = InitialNode();Polypointer c = InitialNode();Polypointer d = InitialNode();Polypointer e = InitialNode();Polypointer f = InitialNode();char* file1 = "Polynomial01.txt";char* file2 = "Polynomial02.txt";char* outfile = "OutPolynomial.txt";CreatePolynomial(a, file1);CreatePolynomial(b, file2);int order;do{Menu(a, b);printf("\n请输入指令:\t");scanf("%d", &order);switch (order){case 0:printf("退出\n");break;case 1:{printf("\nf1+f2=");AddPoly(a, b, c);PrintPoly(c);Write(c, outfile);break;}case 2:{printf("\nf1-f2=");MinusPoly(a, b, d);PrintPoly(d);Write(d, outfile);break;}case 3:{printf("\nf1*f2=");MultiPoly_2(a, b, e);PrintPoly(e);Write(e, outfile);break;}case 4:{int k;do{printf("请输入求导的阶数\n");scanf("%d", &k);} while (k < 0);f = DiffPoly(a, k);printf("d(%d)f1 = ", k);if (f->next) PrintPoly(f);else        printf("0\n");Write(f, outfile);break;}case 5:{printf("请输入x来求值f1（x）\n");double x;scanf("%lf", &x);double value = GetValue(a, x);printf("\nf1(%.2lf) = %.3lf", x, value);break;}default:printf("指令不存在\n");break;}} while (order);return 0;
}void Menu(Polypointer a, Polypointer b)
{printf("\n-----------------------------------\n");printf("链表实现多项式的运算\n");printf("f1 = ");PrintPoly(a);printf("f2 = ");PrintPoly(b);printf("1:加法\n");printf("2:减法 f1-f2\n");printf("3:乘法\n");printf("4:对f1求k阶导\n");printf("5:对f1求值\n");printf("0:退出\n");printf("-----------------------------------\n");return;
}
//创建链表的头节点,初始化链表
Polypointer InitialNode(void)
{Polynode* p = (Polynode*)malloc(sizeof(Polynode));if (p == NULL) return NULL;p->coef = 0;p->exp = 0;p->next = NULL;return p;
}//从文件中读取多项式信息,并创建降序排列的多项式
int CreatePolynomial(Polypointer a, char* filename)
{FILE* fp;fp = fopen(filename, "r");if (fp == NULL){printf("file open failure\n");return Error;}Polynode* q = NULL;while (feof(fp) == 0)          //feof非0表示未到文件末尾{q = (Polynode*)malloc(sizeof(Polynode));    //申请新的节点,把读到的数据放到q指向的节点中if (q == NULL) return Error;q->next = NULL;fscanf(fp, "%f %d", &q->coef, &q->exp);if (q->coef == 0)          //若读到的系数为0，释放该节点{free(q);continue;}Polynode* pre = a;Polynode* cur = a->next;while (cur && q->exp < cur->exp)     //找比q中指数小的节点{pre = cur;cur = pre->next;}if (cur && cur->exp == q->exp)       //若链表中已经存在指数相等节点，系数相加即可{cur->coef = cur->coef + q->coef;free(q);if (cur->coef == 0){pre->next = cur->next;free(cur);}continue;}pre->next = q;      //把q节点接入到链表中q->next = cur;}fclose(fp);return OK;
}//将多项式打印到屏幕上
void PrintPoly(Polypointer a)
{Polynode* p = a->next;while (p){if (p->coef > 0){printf("+");}printf("%.2fx^%d", p->coef, p->exp);p = p->next;}printf("\n");return;
}//为申请的节点赋值，并且链接到pre后面
Polynode* AttachNode(float c, int e, Polynode* pre)
{Polynode* temp = (Polynode*)malloc(sizeof(Polynode));if (temp == NULL)  return NULL;temp->next = NULL;temp->coef = c;temp->exp = e;pre->next = temp;return temp;
}//两个一元多项式相加
void AddPoly(Polypointer a, Polypointer b, Polypointer c)
{Polynode* p1 = a;     //p1指向第一个多项式Polynode* p2 = b;     //p2指向第二个多项式Polynode* cur = c;while (p1 && p2){if (p1->exp > p2->exp){cur = AttachNode(p1->coef, p1->exp, cur);p1 = p1->next;}else if (p2->exp > p1->exp){cur = AttachNode(p2->coef, p2->exp, cur);p2 = p2->next;}else if (p1->exp == p2->exp){float sum = p1->coef + p2->coef;if (fabs(sum) <= 1e-6)   //如果系数和为0{p1 = p1->next;p2 = p2->next;}else{cur = AttachNode(sum, p1->exp, cur);p1 = p1->next;p2 = p2->next;}}}while (p1){cur = AttachNode(p1->coef, p1->exp, cur);p1 = p1->next;}while (p2){cur = AttachNode(p2->coef, p2->exp, cur);p2 = p2->next;}
}//多项式减法 多项式a减多项式b
void MinusPoly(Polypointer a, Polypointer b, Polypointer c)
{Polypointer copyb;copyb = CopyPoly(b);Polynode* p = copyb->next;while (p){p->coef = p->coef * (-1);p = p->next;}AddPoly(a, copyb, c);return;
}//多项式乘法    乘法通过多项式的累加实现
void MultiPoly(Polypointer a, Polypointer b, Polypointer c)
{Polynode* p1 = a->next;Polynode* p2 = b->next;Polynode* p3 = c;//每次用a中的一项乘b中的每一项生成一个临时多项式//将临时多项式与现有的c相加Polypointer headtemp = InitialNode();      //每次生成的多项式的头节点Polynode* ptemp = headtemp;     //ptemp是指向临时多项式当前操作节点的指针while (p1){ClearList(headtemp);ptemp = headtemp;while (p2){Polynode* temp = (Polynode*)malloc(sizeof(Polynode));if (temp == NULL)  return;temp->next = NULL;temp->coef = p1->coef * p2->coef;temp->exp = p1->exp + p2->exp;AttachNode(temp->coef, temp->exp, ptemp);ptemp = ptemp->next;p2 = p2->next;}AddPoly(c, headtemp, c);  //把生成的多项式累加p1 = p1->next;          //p1指向下一项p2 = b->next;           //p2指向b的起始位置}
}//对乘法进行优化，减少频繁的节点分配
//因为每次生成的多项式是相同长度的，所以临时多项式的节点可以反复利用
void MultiPoly_2(Polypointer a, Polypointer b, Polypointer c)
{Polynode* p1 = a->next;Polynode* p2 = b->next;Polynode* p3 = c;Polypointer headtemp = InitialNode();      //临时多项式的头节点Polynode* ptemp = headtemp;     //ptemp是指向临时多项式当前操作节点的指针//先对a中的第一项，生成临时链表if (p1){while (p2){Polynode* temp = (Polynode*)malloc(sizeof(Polynode));if (temp == NULL)  return;temp->next = NULL;temp->coef = p1->coef * p2->coef;temp->exp = p1->exp + p2->exp;AttachNode(temp->coef, temp->exp, ptemp);ptemp = ptemp->next;p2 = p2->next;}AddPoly(c, headtemp, c);  //把生成的多项式累加p1 = p1->next;          //p1指向下一项p2 = b->next;           //p2指向b的第一项}//对临时链表反复利用while (p1){ptemp = headtemp->next;while (p2){ptemp->coef = p1->coef * p2->coef;ptemp->exp = p1->exp + p2->exp;ptemp = ptemp->next;p2 = p2->next;}AddPoly(c, headtemp, c);p1 = p1->next;p2 = b->next;}
}//拷贝给定的多项式
Polypointer CopyPoly(Polypointer a)
{Polypointer b;b = InitialNode();Polynode* p1 = a->next;Polynode* p2 = b;while (p1){Polynode* t = (Polynode*)malloc(sizeof(Polynode));if (t == NULL) return NULL;t->next = NULL;t->coef = p1->coef;t->exp = p1->exp;p2->next = t;p1 = p1->next;p2 = p2->next;}return b;
}//对多项式求k阶导
Polypointer DiffPoly(Polypointer a, int k)
{Polypointer c = CopyPoly(a);    //将多项式a拷贝一份Polynode* p1 = c;   //p1记录着p2的前一个节点Polynode* p2 = c->next;for (int i = 0; i < k; ++i){p1 = c;p2 = c->next;while (p2){p2->coef = p2->coef * p2->exp;p2->exp--;if (p2->exp < 0)       //对常数求导得到的节点需要去掉{p2->coef = 0;p1->next = p2->next;free(p2);p2 = p1->next;}else{p1 = p1->next;p2 = p2->next;}}}return c;
}//求多项式的值
double GetValue(Polypointer a, double x)
{double sum = 0;Polynode* p = a->next;while (p){sum += p->coef * pow(x, p->exp);p = p->next;}return sum;
}//把多项式写入指定文件
int Write(Polypointer a, char* outfile)
{FILE* fp = fopen(outfile, "a");if (fp == NULL){printf("file open failure\n");return Error;}Polynode* p = a->next;while (p){if (p->coef > 0){fprintf(fp, "+");}fprintf(fp, "%.2fx^%d", p->coef, p->exp);p = p->next;}fprintf(fp, "\n");fclose(fp);return OK;
}//清空链表，保存头节点
void ClearList(Polypointer a)
{Polynode* p1 = a->next;Polynode* p2;while (p1){p2 = p1->next;free(p1);p1 = p2;}a->next = NULL;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://xiahunao.cn/news/143314.html

如若内容造成侵权/违法违规/事实不符，请联系瞎胡闹网进行投诉反馈，一经查实，立即删除！

相关文章

c语言一元多项式课程设计,一元多项式的计算数据结构课程设计.doc

c语言一元多项式课程设计,一元多项式的计算数据结构课程设计.doc

一元多项式的计算数据结构课程设计.doc 一元多项式的计算加&#xff0c;减摘要题目一元多项式计算任务能够按照指数降序排列建立并输出多项式&#xff1b;能够完成两个多项式的相加、相减&#xff0c;并将结果输入&#xff1b;目录1引言2需求分析3概要设计4详细设计5测试结果6…
阅读更多...
基于C++的一元多项式相加

基于C++的一元多项式相加

资源下载地址&#xff1a;https://download.csdn.net/download/sheziqiong/85996014 资源下载地址&#xff1a;https://download.csdn.net/download/sheziqiong/85996014 1.实验目的 了解链式存储结构的基本知识&#xff1b;掌握算法思想和数据结构的描述&#xff1b;结合一元…
阅读更多...
c语言一元多项式相加

c语言一元多项式相加

用单链表实现一元多项式相加 #include<stdio.h> #include<stdlib.h> typedef struct Node{float coef;//系数 int exp;//项数 struct Node *next; }LNode,*Linklist;void newPolynomial(Linklist &head){LNode *p;int i,tempExp;float tempCoef;scanf("…
阅读更多...
一元多项式的相乘操作(链表)

一元多项式的相乘操作(链表)

一元多项式的乘法运算如何实现&#xff0c;要求多项式采用链表存储结构。 目录 基本思路&#xff1a; 添加条件的分类&#xff1a; multiple()源代码&#xff1a; detach()源代码&#xff1a; 处理结果&#xff1a; 基本思路&#xff1a; 本篇博客不知觉间已经拖了好久好久…
阅读更多...
数据结构一元多项式的相加-单链表实现

数据结构一元多项式的相加-单链表实现

实验内容&#xff1a;把任意给定的两个一元多项式P(x) ,Q(x) 输入计算机&#xff0c;计算它们的和并输出计算结果。 一元多项式可以用单链表表示&#xff0c;结点结构图示如下&#xff1a; coef expnext 首先分析一下这个过程是如何实现的 该算法需要求A与B两个一元多项式的和&…
阅读更多...
一元多项式加减乘实现c/c++

一元多项式加减乘实现c/c++

一、实验题目&#xff1a; 一元多项式简单的计算器 1.主要功能&#xff1a; (1)输入并建立多项式&#xff1b; (2)输出多项式&#xff1b; (3)两个多项式相加&#xff0c;建立并输出和多项式&#xff1b; (4)两个多项式相减&#xff0c;建立并输出差多项式。 (5)算法的时…
阅读更多...
一元多项式的加法

一元多项式的加法

一元多项式的加法 问题描述&#xff1a;一元多项式的加法 &#xff08;1&#xff09; 编程实现一元多项式的加法。 &#xff08;2&#xff09; 编写一个测试主函数。 分析&#xff1a; 对于任意一元多项式 可以抽象为一个由“系数—指数”对构成的线性表&#xff0c;且线性表中…
阅读更多...
一元多项式求导

一元多项式求导

问题描述&#xff1a; 设计函数求一元多项式的导数。&#xff08;注&#xff1a;x​n​​&#xff08;n为整数&#xff09;的一阶导数为nx​n−1​​。&#xff09; #include<cstdio> int main() {int a[100000];int b[100000];int n,m;char c;//判断结束的条件scanf(&q…
阅读更多...
一元多项式课设

一元多项式课设

代码详见 目录 一、实习任务........................................................................................... - 1 - 1.问题描述&#xff1a;.................................................................................... - 1 - 2.小组分工.........…
阅读更多...
数据结构：一元多项式及其基本运算

数据结构：一元多项式及其基本运算

1、实现方式&#xff1a;可采用线性表的顺序存储结构&#xff0c;但是当多项式的每个项的指数差别很大时&#xff0c;会浪费很多存储空间。所以采用链式存储方式表示&#xff0c;每一项可以表示成一个结点&#xff0c;结点的结构由存放系数的coef域&#xff0c;存放指数的expn域…
阅读更多...
一元多项式计算

一元多项式计算

目录 题目的内容及要求--------------------------------------------2需求分析-------------------------------------------------------2概要设计-------------------------------------------------------2 1、存储结构------------------------------------------------…
阅读更多...
【数据结构】一元多项式的表示及相加

【数据结构】一元多项式的表示及相加

文章目录 ⭐️写在前面的话⭐️一元多项式的表示及相加初始化0_1、初始化链表0_2_1、头插法插入多项式的项(没有相同项)0_2_2、将要插入的相同&#xff0c;链表中有相同项&#xff0c;对应系数相加0_3、从链表中查找是否有相同的指数项0_4、对已经创建好的一元多项式按指数大小…
阅读更多...
数据结构（严蔚敏）【一元多项式的运算】【C语言】

数据结构（严蔚敏）【一元多项式的运算】【C语言】

1、一元多项式的运算&#xff1a;实现两个多项式加、减乘运算 设计内容&#xff1a; 用顺序存储结构实现一元多项式的加法、减法和乘法。具体要求为&#xff1a;用五个函数分别实现一元多项式的创建、输出、加法、减法和乘法&#xff1b; 设计思路&#xff1a; 将顺序表数组…
阅读更多...
算法竞赛入门【码蹄集进阶塔335题】(MT2151-2175）

算法竞赛入门【码蹄集进阶塔335题】(MT2151-2175）

算法竞赛入门【码蹄集进阶塔335题】(MT2151-2175&#xff09; 文章目录 算法竞赛入门【码蹄集进阶塔335题】(MT2151-2175&#xff09;前言为什么突然想学算法了&#xff1f;为什么选择码蹄集作为刷题软件&#xff1f; 目录1. MT2151 权值计算2. MT2152 黑客小码哥3. MT2153 来给…
阅读更多...
Linux基础之LVM卷管理

Linux基础之LVM卷管理

LVM LVM是 Logical Volume Manager&#xff08;逻辑卷管理&#xff09;的简写&#xff0c;它是Linux环境下对磁盘分区进行管理的一种机制。Linux用户安装Linux操作系统时遇到的一个常见的难以决定的问题就是如何正确地评估各分区大小&#xff0c;以分配合适的硬盘空间。普通的…
阅读更多...
linux lvcreate,LFCS：如何使用vgcreate，lvcreate和lvextend命令管理和创建LVM - 第11部分...

linux lvcreate,LFCS：如何使用vgcreate，lvcreate和lvextend命令管理和创建LVM - 第11部分...

因为在LFCS考试要求有效的二月变化 2&#xff0c;2016年 &#xff0c;我们增加了必要的专题到LFCS系列发表在这里。 为了准备这场考试&#xff0c;你是高度鼓励使用联邦经济竞争法系列为好。 LFCS&#xff1a;管理LVM和创建LVM分区 - 第11部分 安装Linux系统时最重要的决定之一…
阅读更多...
lvm 制作

lvm 制作

壹&#xff1a; 创建LVM 逻辑卷 1&#xff0c;将物理盘格式为pv卷&#xff08;物理卷&#xff09;&#xff0c;使用pvcreate 命令 pvcreate /dev/sdc 或则是 pvcreate /dev/sdc /dev/sdb pvdisplay 或pvs 命令查看 PV 物理卷得创建情况 2,创建卷组 VG 通过vgcreate 命令,将pv加…
阅读更多...
lvcreate 常用命令举例

lvcreate 常用命令举例

http://linux.cn/article-5117-1.html4 个 lvcreate 常用命令举例 2015-3-25 15:09| 查看: 2752| 评论: 3| 收藏: 3| 分享: 10 原文&#xff1a;http://www.ehowstuff.com/4-lvcreate-command-examples-on-linux/作者&#xff1a; skytech译文&#xff1a;LCTT https://linux.…
阅读更多...
49.逻辑卷管理4,逻辑卷管理详解,lvscan,lvcreate,lvdisplay,lvextend,lvreduce,lvremove,lvresize,lvchange

49.逻辑卷管理4,逻辑卷管理详解,lvscan,lvcreate,lvdisplay,lvextend,lvreduce,lvremove,lvresize,lvchange

逻辑卷相关操作 可以把逻辑卷想象成分区&#xff0c;那么这个逻辑卷当然也需要被格式化和挂载。另外&#xff0c;逻辑卷也是可以动态调整大小的&#xff0c;而且数据不会丟失&#xff0c;也不用卸载逻辑卷。 常用的命令有 lvscan Lvcreate Lvdisplay lvextend lvreduce Lvremov…
阅读更多...
oppo手机删除计算机怎样恢复,【数据恢复篇】oppo手机删掉的照片怎么恢复

oppo手机删除计算机怎样恢复,【数据恢复篇】oppo手机删掉的照片怎么恢复

原标题&#xff1a;【数据恢复篇】oppo手机删掉的照片怎么恢复 手机删掉的照片可以恢复吗&#xff1f;oppo手机删掉的照片怎么恢复&#xff1f;很多人会奇怪oppo手机删掉的照片还能恢复吗&#xff1f;现在科技技术的提高&#xff0c;照片能够被恢复也是很简单的。像我们所知道的…
阅读更多...
最新文章

Copyright @ 2022~2023