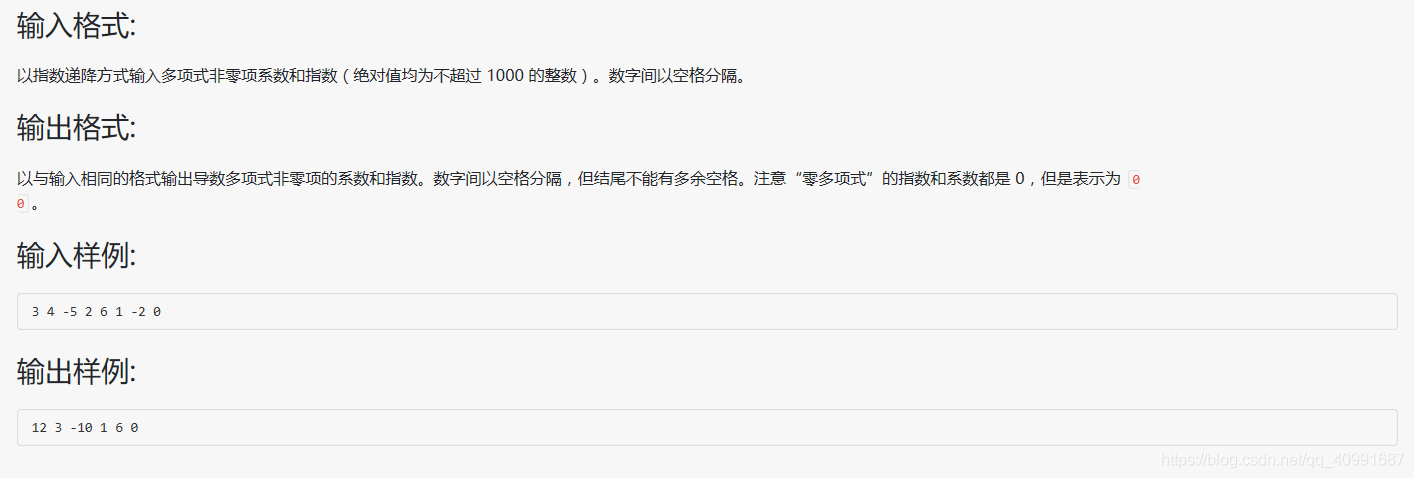
一元多项式的加法
问题描述:一元多项式的加法
(1) 编程实现一元多项式的加法。
(2) 编写一个测试主函数。
分析:
对于任意一元多项式
可以抽象为一个由“系数—指数”对构成的线性表,且线性表中各元素的指数项是递增的
P=((P0,0),(P1,1),(P2,2),~,(Pn,n))
用单链表储存多项式的结点结构,其结构为:
Typedef dtruct node{
float coef; //系数域
int exp; //指数域
struct node *next; //指针域
}PloyNode,*Polylist;

要点:
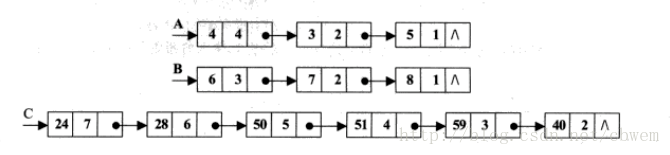
两个多项式相加
1、若p->expexp
则结点p所指的结点应是“和多项式”中的-项,令指针p后移;
2、若p->exp=q->exp
则将两个结点中的系数相加,当和不为零时修改结点p的系数域,释放q结点;
若和为零,则和多项式中无此项,从A中删去p结点,同时释放p和q结点;
3、若p->exp>q->exp
则结点q所指的结点应是“和多项式”中的一项,将结点q插入在结点p之前,且令指针q在原来的链表上后移。
2.概要设计
程序包括的模块:
建立n项一元多项式链表:Polylist Polycreate(int n);
多项式相加:void AddPolyn(Polylist polya, Polylist polyb, Polylist& polyc);
输出:void PrintPolyn(Polylist L, int n);
各函数间调用关系图:
3.详细设计
(1)定义结构体Polynode:
typedef struct Polynode {int coef;int exp;struct Polynode* next;
}Polynode, * Polylist;
(2) 实现方法
1、建立一个n项一元多项式链表:
Polylist Polycreate(int n)
{Polylist head, rear, s;int c = 1, e, i = 1;head = (Polylist)malloc(sizeof(Polynode));rear = head;while (c != 0 && i <= n){i++;scanf_s("%d,%d", &c, &e);s = (Polylist)malloc(sizeof(Polynode));s->coef = c;s->exp = e;rear->next = s;rear = s;}rear->next = NULL;return head;
}
2、相加后给polyc:
void AddPolyn(Polylist polya, Polylist polyb, Polylist& polyc)
{int sum = 0;Polylist r, Lc;polyc = Lc = polya;polya = polya->next;polyb = polyb->next;while (polya != NULL && polyb != NULL){if (polya->exp < polyb->exp){Lc->next = polya;Lc = polya;polya = polya->next;}else if (polya->exp == polyb->exp){sum = polya->coef + polyb->coef;if (sum != 0){polya->coef = sum;Lc->next = polya;Lc = polya;polya = polya->next;r = polyb;polyb = polyb->next;free(r);}else{r = polya;polya = polya->next;free(r);r = polyb;polyb = polyb->next;free(r);}}else{Lc->next = polyb;Lc = polyb;polyb = polyb->next;}}Lc->next = polya ? polya : polyb;}
3、输出
void PrintPolyn(Polylist L, int n)
{Polylist p;int i = 0;p = L->next;while (p && i < n){i++;printf("(%d,%d) ", p->coef, p->exp);p = p->next;}printf("\n");
}
4.调试与分析
(1)函数:

(2)结果:

5.总结
1、可以根据运算确定使用什么数据结构,如不改变系数和指数的运算,采用顺序存储结构;改变系数和指数的运算,采用链式存储结构。.
2、像本题也可以在pa后直接插入pb中多余项。不用在写一个pc,可以简便一下代码。## 标题