目录
- 题目的内容及要求--------------------------------------------2
- 需求分析-------------------------------------------------------2
- 概要设计-------------------------------------------------------2
1、存储结构-----------------------------------------------------------2
2、主程序结构图-----------------------------------------------------3
3、程序函数构成详细设计--------------------------------------4
1、读取-----------------------------------------------------------------4
2、排列-----------------------------------------------------------------5
3、输出-----------------------------------------------------------------6
4、加法-----------------------------------------------------------------6
5、减法------------------------------------------------------------------7
- 源代码-----------------------------------------------------------8
- 运行结果及分析-----------------------------------------------17
七、收获及体会,总结--------------------------------------------20
一、题目的内容及要求
【问题描述】
1.能够按照指数降序排列建立并输出多项式;
2.能够完成两个多项式的相加、相减,并将结果输入;
【任务要求】
1.存储结构;
2.多项式相加的基本过程的算法(可以使用程序流程图)
3.可以提出算法的改进方法;
【测试数据】
自行设定,注意边界等特殊情况。
二、需求分析
而需要做的就是能够按照指数降序排列,建立并输出多项式;能够完成两个多项式的相加、相减,并将结果输出
三、概要设计
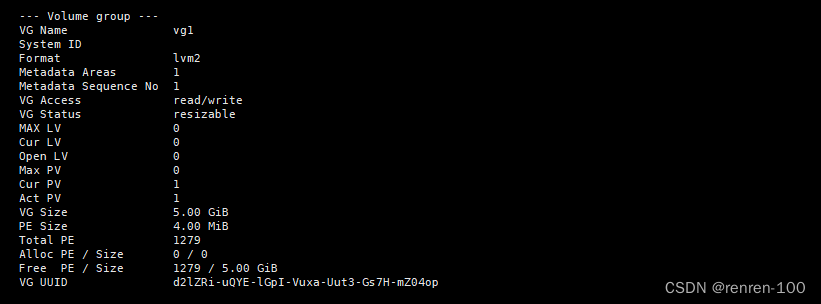
1、存储结构
在数学上,一元多项式P(x)的表示为:
P(x)=a0+a1x+a2x2+…+anxn
其中,n为大于或等于0的整数,表示x的幂:a0,a1,…an为系数,an≠0,a0,a1,…,an-1可以为0,也可以不为0根据一元多项式相加的运算规则:
对于两个一元多项式中所有指数相同的项,对应指数相加(减),若其和(差)不为零,则构成“和(差)多项式”中的一项对于两个一元多项式中所有指数不相同的项,则分别写到“和(差)多项式”中去。此程序的数据结构是选择用不带头结点的单链表存储多项式。虽然一元多项式可以采用顺序和链式两种存储结构,因为多项式指数最高项以及项数是不确定的,使用顺序表就会浪费巨大的存储空间,因此采用线性链表的存储结构便于实现一元多项式的运算。单链表的结构体可以用来存储多项式系数,指数和指向下一个节点的指针。
系数域 指数域 指针域
| coef | exp | next |
typedef struct pnode
{
float coef;
int exp;
struct pnode *next;
}pnode;
2、主程序功能结构图

3、程序函数构成
pnode *creat()读取并创建一个多项式链表
void sort(pnode *head)对多项式进行排列
pnode * add(pnode *heada,pnode *headb)多项式和的计算
pnode * sub(pnode *heada,pnode *headb)多项式差的计算
void outlink(pnode *head)存储一个多项式链表
void display(pnode *head)输出一个多项式链表
void add_main()加法函数
void sub_main()减法函数
void showmenu菜单函数
void main主函数主要负责输出界面的指引语句,并合理地调用各个函数,还要有适当的循环操作以及停止循环的语句,以致可以方便地达到合并两个一元多项式的功能。
四、详细设计
1、读取:
从文件中读取多项式的系数与指数并存入链表。当创建多项式时,利用for循环从文件读出数据后,插入尾部的方式将多项式的数据连接起来,直到遍历完所有数据时停止。
pnode *creat1()
{
FILE *fp;
int item,i;
char filename[20];
pnode *tail, *Temp;
tail=&head;
Temp=&head;
printf("请输入文件名");
gets(filename);
fp=fopen(filename,"r");
fscanf(fp,"%d",&item);
for(i=0;i<item;i++)
{
pnode *p=(pnode *)malloc(sizeof(pnode));
fscanf(fp,"%f%d",&(p->coef),&(p->exp));
tail->next=p;
p->next=NULL;
tail=p;
}
fclose(fp);
return Temp->next;
}
读取函数的流程图:

2、排列
根据要求对指数进行降序排列,先定义三个临时指针和一个用来交换数据的变量,利用简单选择排序的思想,从n个数据通过指针中找到最大值,通过变量temp来交换两个结点中的数据,把最大的放在链表最首端,再从剩下的n-1个数据中找最大值,然后放在n-1个数据的链表最首位
void sort(pnode *head)
{
pnode *p,*q,*t;
float temp;
p=head;
while(p!=NULL)
{
q=p;
t=q->next;
while(t!=NULL)
{
if(t->exp>q->exp)
q=t;
t=t->next;
}
temp=p->coef;p->coef=q->coef;q->coef=temp;
temp=p->exp;p->exp=q->exp;q->exp=temp;
p=p->next;
}
}
这个算法缺点也很明显,虽然“简单”,但效率不高,原因主要在于大量的冗余比较。因为简单选择排序并不能记住每次比较的结果,如果已经知道a<b并且b<c,再比较c和c是没意义的。另外,一旦确定两个元素的大小,那么再进行重复比较也是没意义的。
3、输出
为了直观地了解链表的内容,我们设计出依次输出链表结点的函数。由于该题目对链表的输出格式又有了一定的要求,因此该函数设计也有着不一样的地方。依题意得;首先输出系数,系数后面紧跟着一个符号”X”;再输出指数,指数的前面带有符号”^”;而且相邻的结点都要用”+”或”-”链接起来,因此我们还要对系数的正负进行判断(由于头地址比较特殊,所以头地址除外)。系数为正,要输出符号”+”;系数为负时,编译时会自动加入符号”-”,所以不必再输出符号”-”
1) 建立一个新的指针变量,并把头指针赋给它;
2) 如果为空,则打印出”全空”的语句;
3) 由于该程序没有删除结点的函数,所以碰到系数为”0”时,我们直接跳到步骤7;
4) 否则,先以”系数x ^指数”的形式输出头结点的成员;
5) 若还要继续输出结点,就判断系数的正负;
若系数为正,以”+ 系数x ^指数” 的形式输出;
若系数为负,以” 系数x ^指数” 的形式输出;
- 把新指针指向下一个结点;
7) 若还要继续输出结点,转到步骤3继续执行;
8) 否则,结束程序。
4、加法
以单链表pa和pb分别表示两个元多项式A和B, A+B的求和运算,就等同于单链表的插入问题,为了方便演示程序,我们设-一个单链表pc来存放pa+pb的和。
设qa,qb,qc分别指向单链表pa,pb,pc的当前项,比较qaqb结点的指数项由此可得到以下:
a:若qa->exp<qb >exp,则结点qa所指向的结点应是“和多项式”中的一项,将qa复制到qc中,令指针qa后移。
b:若qa->exp=qb->exp,则将两个结点中的系数相加,当和不为0时,qa的系数域加qb的系数域作为qc的系数域:若和为0,则“和多项式”中无此项,qa和qb后移。
C:若qa->exp>qb->exp,则结点qb所指向的结点应是“和多项式”中的一项,将qb复制到qc中,令指针qb后移。
5、减法
将减数pb多项式的系数取反,然后使用相加的方法处理
五、源代码
详细原文和源代码请点击链接下载
https://download.csdn.net/download/weixin_57836618/77831214