一元多项式的乘法运算如何实现,要求多项式采用链表存储结构。
目录
基本思路:
添加条件的分类:
multiple()源代码:
detach()源代码:
处理结果:
基本思路:
本篇博客不知觉间已经拖了好久好久了,接上一篇博客:一元多项式的相加和相减操作,就让我继续为各位讲解一下一元多项式的相乘操作。
为了实现相乘操作,最简单且有效的办法是先用一个多项式(后文称为多项式A)的每个单项式与另外一个多项式(后文称为多项式B)的首个多项式分别相乘,建立代表结果的多项式的初始多项式(也可能是单项式,这里可以不予讨论,结果并不会因为初始的结果是单项式就变得不正确,故统一认为是多项式)。然后,如果多项式B有第二项,那么将它的第二项再次分别与多项式A的各项相乘,在每一次相乘后将得到的结果单项式加入到初始多项式中,不断地更新得到的储存结果的多项式,该过程持续到多项式B的最后一项。
在有了以上的基本思路后,我们剩下要讨论的点就很清晰明确了:该如何实现向初始多项式中添加单项式的操作呢?或者,应当把问题更明确地说为:如何确定新得到的单项式加入多项式某处的条件?
初始多项式可能要为存储这个新的单项式而开辟一个新的位置,原因是多项式中没有和这个新的单项式的指数相同的单项式,否则就不用开辟,直接将这个新单项式与这个多项式里面对应的单项式相加后将结果存入多项式中的单项式即可,而这也可能导致一个问题:两个单项式相加后的结果的系数可能为 0 ,对于这样的情况,先不讨论,在本篇博客稍后的部分再进行讨论。
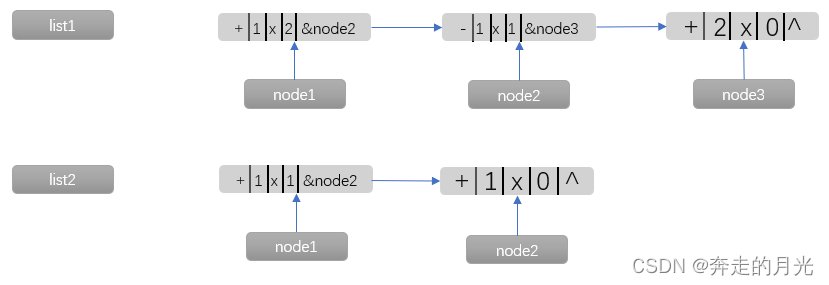
对于以上过程,以a(x)=x^2-x+2与b(x)=x+1为例:
这是两个多项式的结构图示,将多项式b(x)的首项与多项式a(x)的各项分别相乘得到初始多项式c(x),其图示为:
然后,由于b(x)有第二项,我们用b(x)的第二项再次与a(x)的各项相乘,得到第一个单项式(x^2*1):
初始多项式中有指数为2的单项式,故一个新的多项式为:
可以看到,指数为2的这一项的系数变为0了,再将第二个单项式(-x*1)即
放入多项式中,多项式中有指数为1的单项式,故多项式变为:
第三个单项式(2*1):
多项式中没有指数为0的单项式,其单项式指数最小为1,故将该单项式连接在多项式最后一项的后面:
至于list3中的node2如何去掉,后文会介绍方法。
添加条件的分类:
现在就让我们细分一下向初始多项式添加单项式的条件,在这之前,我们将得到的单项式存入被称为temp的结点中。在我们得到初始的多项式时,将其存入list4中,再用一个搜索指针temp4指向list4中的结点,temp4的初值为list4中的首结点的地址,在每一轮搜索后都要为其重新赋该地址值。
可以向初始的list4或是正在变化的list4的哪些地方添加这个单项式的值呢?分为三类:
1、链表的结点处
2、链表的结点间
3、链表的末尾
对于第1种情况,这是很合理的,但并不是总能出现这种情况,其成立的条件是在链表中有单项式与将被添加的单项式具有相同指数;第2种情况的出现则是因为在链表中刚好有相邻两个结点的指数分别大于和小于将被添加的单项式的指数的;第3种情况,原因在于链表的所有结点代表的单项式的指数均大于将被添加的单项式的指数,那么该结点就只能连接到链表末尾了。这三种情况产生的前置条件均是建立在多项式是按照降幂顺序排列的基础上的。
上述的条件大致可以转化成这样的结构:
//代码清单1
//将被添加的单项式被存储在temp指向的内存区域中
while(1)
{if (temp->exp < temp4->exp){//判断temp4的下一个结点是否为空,即判断搜索指针temp4是否到达了list4的最后一个结点//若是,将temp连接到list4末尾,然后结束while循环,对应上述第3种情况//若不是,使得搜索指针temp4指向list4的下一个结点}else if (temp->exp > temp4->exp){//将temp指向的结点连接在temp4指向的结点以及该结点的前一个结点//之间,然后结束while循环,对应上述第2种情况}else{//将temp4、temp代表的单项式相加后的结果存入temp4中,然后结束//while循环,对应上述第1种情况}
}multiple()源代码:
//代码清单2
void multiple(poly *head1, poly *head2)
{//将head1和head2指向的链表代表的多项式相乘后的结果存储在head4指向的list4中poly *head4 = (poly*)malloc(sizeof(poly));//temp4和temp_ptr用来建立初始链表 poly *temp4 = head4;poly *temp4_ptr = NULL;//temp1和temp2分别用作遍历list1和list2过程中的搜索指针poly *temp1 = head1;poly *temp2 = head2;//temp指向代表存储temp1、temp2代表的单项式相乘结果的结点,只是暂时储存poly *temp = (poly*)malloc(sizeof(poly));//pre代表temp4指向结点的前一个结点(指的是在该代码清单//第37行开始的while循环中),在处理第2种情况时会有用处poly *pre = head4;while (temp1 != NULL){temp4->sign = temp1->sign != temp2->sign ? '-' : '+';temp4->coef = temp1->coef*temp2->coef;temp4->exp = temp1->exp + temp2->exp;temp4->alph = head1->alph;temp4_ptr = temp4;temp4 = (poly*)malloc(sizeof(poly));temp4_ptr->next = temp4;temp1 = temp1->next;}temp4_ptr->next = NULL;free(temp4);temp4 = NULL;temp1 = head1;temp2 = head2->next;temp4 = head4;while (temp2 != NULL){while (temp1 != NULL){temp->sign = temp1->sign != temp2->sign ? '-' : '+';temp->coef = temp1->coef*temp2->coef;temp->alph = head1->alph;temp->exp = temp1->exp + temp2->exp;while (1){if (temp->exp < temp4->exp){if (temp4->next == NULL){temp4->next = temp;temp->next = NULL;temp = (poly*)malloc(sizeof(poly));break;}pre = temp4;temp4 = temp4->next;}else if (temp->exp > temp4->exp){pre->next = temp;temp->next = temp4;temp = (poly*)malloc(sizeof(poly));break;}else{temp->coef = temp->sign == '+' ? temp->coef : -temp->coef;temp4->coef = temp4->sign == '+' ? temp4->coef : -temp4->coef;temp4->coef = temp->coef + temp4->coef;temp4->sign = temp4->coef > 0 ? '+' : '-';temp4->coef = abs(temp4->coef);break;}}temp1 = temp1->next;}temp2 = temp2->next;temp1 = head1;temp4 = head4;}free(temp);temp = NULL;output(head4);
}先不着急讲解,我们可以测试一下这个代码:
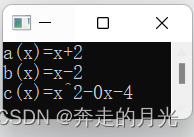
结果是符合我们预期的,美中不足的是c(x)中的"-0x"不太美观哈,但这不要紧,后面我们将想办法去掉,由于这种情况的产生源于多项式相乘过程中指数相同的两项的系数互为相反数,也许你会想到在执行第1种情况的代码中利用pre指针将系数为0的这一项移除,但这并不是更好的方法,想一想,如果你将两个多项式的值都设置为多个系数为0的单项式的和,结果会使得list4一直重复去除系数为0的单项式,而最后整个结果也为0,接下来是不是要将list4置空?这样会使得list4代表的结果即0无法被打印出来,所以我觉得最好的方法是建立一个函数,通过这种方法会使得我们的思路简化很多。
代码清单2第18至32行用于建立初始链表,而由于我们采用的建立初始链表list4的方法是将list2代表的多项式的首项与list1代表的多项式的每一项相乘得到,所以在34行开始让temp1重新指向list1的首结点,让temp2指向list2的首结点的后一个结点(可能为NULL,不要紧),让temp4指向list4的首结点。第37和39行开始的while循环注意次序,第76行对应内层的while循环,第78至80行间的代码则对应外层的。第41至44行的代码用于建立temp指向的结点。第45至75行的循环设置为类似死循环的循环结构是因为有可以结束这个循环的条件,也就是说最终能把temp指向的结点成功填入list4中。
detach()源代码:
//代码清单3
poly *detach(poly *head)
{poly *temp = NULL;poly *pre = head;while (head->coef == 0){if (head->next == NULL)break;head = head->next;free(pre);pre = head;}temp = head->next;pre = head;while (temp != NULL){while (temp->coef == 0){temp = temp->next;free(pre->next);if (temp != NULL)pre->next = temp;else{pre->next = NULL;return head;}}pre = temp;temp = temp->next;}return head;
}如何去除存储相乘结果的链表中的代表系数为0的单项式的结点呢?为此,detach()函数被写了出来。我的想法是这样的:如果list4(假设有多个结点)中前几个结点代表系数为零的单项式,那么我们在将这几个结点从list4中去除后,选择list4中的第一个非零结点作为首结点,以此为起点,继续用搜索指针一步步后移将之后的零结点去除,直到搜索指针指向NULL,即整条链表被遍历完全。
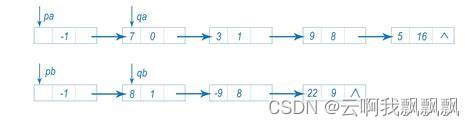
代码清单3第6至13行的代码,就像我前面提到的,它的主要作用是去除list4中的前几个零结点,如果有的话,没有的话自然就不执行,例如下图:

在将node1删除后,node1后续几个结点依次前移,形成新的list4。然后就是第8至9行的if判断结构,它是十分重要的,体现在以下情况:
1、list4只有一个结点,list4代表着一个系数为0的单项式
2、list4具有多个结点,但每个结点代表的系数均为0,list4代表着一个零多项式
所以,在符合两种情况之一时,这个判断结构保证能够为list4保留一个结点。那么保留的结点是list4中的哪个结点呢?对于第一种情况,不必多说;对于第二种情况,则会将list4中的最后一个结点保留下来。第14行代码中temp的值可能为NULL,原因就在于这两种情况 ,这样的话也就不会执行第16至32行的while循环了。说到第16至32行的while循环,它就是用来处理list4中已经确定的非零结点后面的零结点的,例如下图:

以node1为起点,历经node2,发现后续几个结点都是零结点,直到node5,那么这个while循环会将node3、node4删除,node5、node6会变成新的node3、node4。当然,list4的末尾几个结点也有可能是零结点,处理的方法是一样的。
处理结果:
既然detach()函数写好了,我们将它添入multiple()函数的第83行和第84行语句的中间,执行一下,运行结果为:
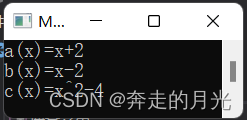
结果是很OK的。
欢迎指正我的上一篇博客:一元多项式的相加和相减操作(链表)
我的下一篇博客:待续