一、实验题目:
一元多项式简单的计算器
1.主要功能:
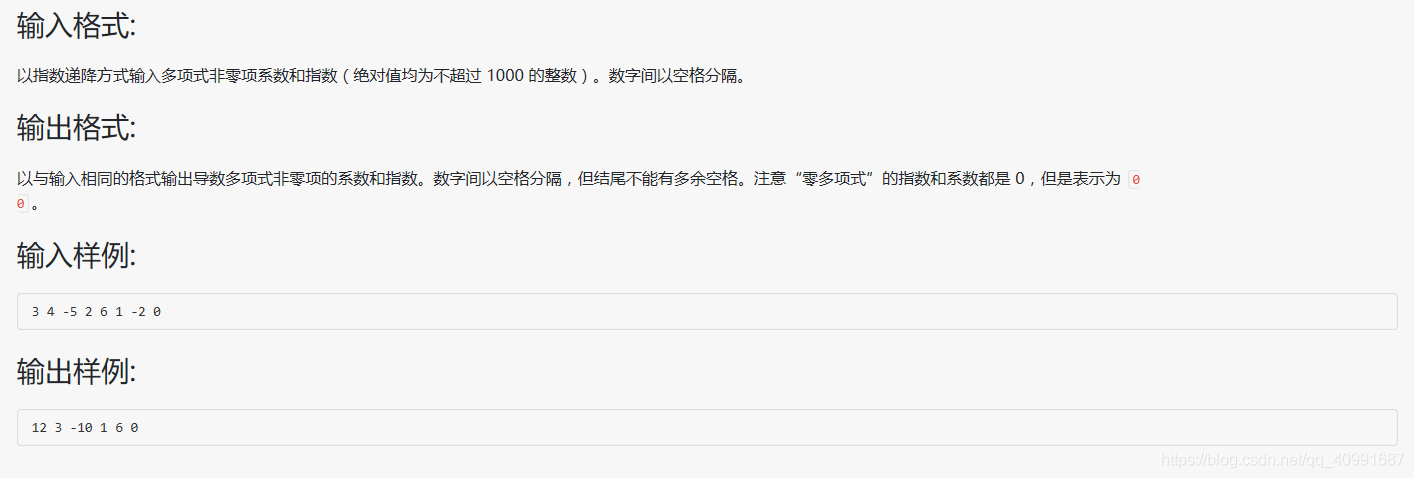
(1)输入并建立多项式;
(2)输出多项式;
(3)两个多项式相加,建立并输出和多项式;
(4)两个多项式相减,建立并输出差多项式。
(5)算法的时间复杂度、另外可以提出算法的改进方法
实现提示:可选择带头结点的单向循环链表或单链表存储多项式,头结点可存放多项式的参数,如项数等。
2.要求:一元多项式简单计算器的基本功能
二、代码
1.全局变量和主函数:
#include<iostream>
using namespace std;
const double T= 0.000001;//用于比较两个double类型的数是否相等;double xs1[1000], xs2[1000], cs1[1000], cs2[1000];//储存两个一元多项式的系数和次数的数组
int n1, n2;//两个一元多项式的项数;
char x;//运算字符(“+”,“-”,“*”)//储存每一项的系数和项数
struct term {double a;//系数double b;//次数term* next, * prior;
};int main() {int flag = 0;while (1) {//输入input();//创建链表term *poly1= creat(xs1, cs1, n1);term *poly2 = creat(xs2, cs2, n2);term* poly=NULL;//计算loop:switch (x) {case '+':poly = add(poly1, poly2);break;case '-':poly = subtract(poly1, poly2);break;case '*':poly = multiply(poly1, poly2);break;case '>':flag = 1;break;default:cout << "暂时不提供该运算" << endl;cin >> x;goto loop;}//输出if (flag) {output(poly1);output(poly2);}elseoutput(poly);}return 0;
}
2.创建多项式
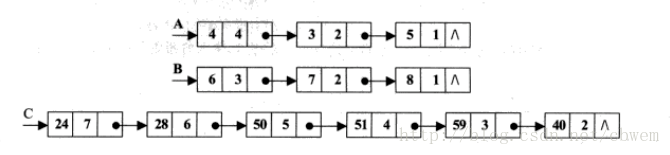
用双向链表表示一元多项式:头节点储存一元多项式的项数,创建新节点储存每一项的系数和次数,新节点的插入从头节点开始比遍历,找到次数大于新节点的节点,插入这个节点的前面。
*链表有序:方便后续的运算的实现
*双向链表:在插入时,需要找前驱节点,不用再次遍历链表,减小找时间复杂度。
这里其实还可以改进,找插入点时直接这样找:
while(q->next==NULL&&q->next->b>p->b){//……………………………………
}这样就不用找前驱节点。
/*
目的:创建双向链表储存一元多项式;
输入参数:储存次数和系数的数组,项数;
返回值:有序(按次数小到大)的双向链表的头指针;
*/
term* creat(double xs[], double cs[], int n) {term* head, * p = NULL, * q = NULL;int i = 0;head = new term;head->a = n, head->b = 0;head->next = NULL;head->prior = NULL;q = head;while (i < n) {p = new term;p->a = xs[i];p->b = cs[i++];while (q != NULL && q->b < p->b) {q = q->next;}if (q == NULL) {q = head;while (q->next != NULL)q = q->next;p->next = NULL;p->prior = q;q->next = p;}else {p->next = q;q->prior->next = p;p->prior = q->prior;q->prior = p;}q = head;}return head;
}2.加减乘实现
加法运算:
创建新链表储存结果,将两个一元多项式的链表从头开始遍历,链表1和链表2比较次数,如果相等,将两个的系数相加的结果和系数按顺序插入新链表。将新节点插入新链表时,如果新链表中有次数与新节点相同,则直接将新节点的系数与该节点的系数相加。如果链表1的系数大,链表2进入下一个节点,直到链表1的系数小于链表2的系数,链表1进入下一个节点。直到有链表遍历完,将另一个链表的节点插入新链表。
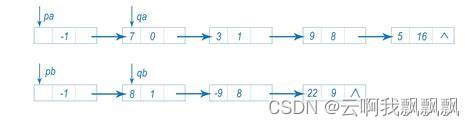
其他的运算类似。
/*
目的:将两个一元多项式相加;
输入参数:两个一元多项式的链表头指针;
返回值:相加后的一元多项式的链表头指针;
*/
term* add(term* p1, term* p2) {p1 = p1->next, p2 = p2->next;term* head, * p, * q;head = new term;head->a = 0, head->b = 0;head->next = NULL;head->prior = NULL;q = head;while (p1 != NULL && p2 != NULL) {p = new term;if (p1->b- p2->b<T) {p->b = p1->b;p->a = p1->a + p2->a;p1 = p1->next;p2 = p2->next;}else if (p1->b < p2->b) {p->b = p1->b;p->a = p1->a;p1 = p1->next;}else {p->b = p2->b;p->a = p2->a;p2 = p2->next;}head = insert(p, head);}if (p1 == NULL) {while (p2 != NULL) {p = new term;p->b = p2->b;p->a = p2->a;head = insert(p, head);p2 = p2->next;}}if (p2 == NULL) {while (p1 != NULL) {p = new term;p->b = p1->b;p->a = p1->a;head = insert(p, head);p1 = p1->next;}}head->a = 0;head->b = 0;return head;
}/*
目的:将两个一元多项式相减
输入参数:两个一元多项式的链表头指针;
返回值:相减后的一元多项式的链表头指针;
*/
term* subtract(term* p1, term* p2) {p1 = p1->next, p2 = p2->next;term* head, * p, * q;head = new term;head->a = 0, head->b = 0;head->next = NULL;head->prior = NULL;q = head;while (p1 != NULL && p2 != NULL) {p = new term;if (p1->b - p2->b<T) {p->b = p1->b;p->a = p1->a - p2->a;p1 = p1->next;p2 = p2->next;}else if (p1->b < p2->b) {p->b = p1->b;p->a = p1->a;p1 = p1->next;}else {p->b = p2->b;p->a = -p2->a;p2 = p2->next;}head = insert(p, head);}if (p1 == NULL) {while (p2 != NULL) {p = new term;p->b = p2->b;p->a = -p2->a;head = insert(p, head);p2 = p2->next;}}if (p2 == NULL) {while (p1 != NULL) {p = new term;p->b = p1->b;p->a = p1->a;head = insert(p, head);p1 = p1->next;} }head->a = 0;head->b = 0;return head;
}/*
目的:将两个一元多项式相乘
输入参数:两个一元多项式的链表头指针;
返回值:相乘后的一元多项式的链表头指针;
*/
term* multiply(term* p1, term* p2) {term* P2 = p2;p1 = p1->next, p2 = p2->next;term* head, * p, * q;head = new term;head->a = 0, head->b = 0;head->next = NULL;head->prior = NULL;q = head;while (p1 != NULL) {while (p2 != NULL) {p = new term;p->a = p1->a * p2->a;p->b = p1->b + p2->b;head = insert(p, head);p2 = p2->next;}p2 = P2->next;p1 = p1->next;}head->a = 0;head->b = 0;return head;
}/*
目的:输入要计算的两个一元多项式的系数、次数和项数;
输入参数:无;
返回值:无;
*/新节点插入链表:
重用率最高的模块,极大的缩减代码篇幅。同时该函数也能确保结果链表依然保持有序。能对不同插入位置(链表尾,链表中)进行处理,能判断要插入的链表中是否有次数相同的节点,避免链表出现相同次数的节点。
/*
目的:将节点有序的插入链表;
输入参数:要插入的节点,被插入的链表头节点;
返回值:插入后的链表的头节点;
*/
term* insert(term* p, term* head) {term *q = head;while (q != NULL && q->b < p->b) {q = q->next;}if (q == NULL) {q = head;while (q->next != NULL)q = q->next;p->next = NULL;p->prior = q;q->next = p;}else if (q->b - p->b < T) {q->a += p->a;}else {p->next = q;p->prior = q->prior;q->prior->next = p;q->prior = p;}return head;
}3.输入输出
提示输入信息,获取两个一元多项式的次数、系数和项数,次数和项数用数组储存。变量和数组均为全局变量,便于后续数据传递。
输出时按要求打印输出即可。对一些特殊情况分类讨论,如次数或系数为1或0时输出的处理,结果为0时的输出处理。
/*
目的:输入要计算的两个一元多项式的系数、次数和项数;
输入参数:无;
返回值:无;
*/
void input() {cout << "请输入第一个一元多项式的项数:";cin >> n1;if (n1 >= 1000) {cout << "项数过多,请重新输入:";cin >> n1;}cout << "请输入每一项的系数:" << endl;for (int i = 0;i < n1;i++) {cin >> xs1[i];}cout << "请输入对应项数的次数:" << endl;for (int i = 0;i < n1;i++) {cin >> cs1[i];}cout << endl << "请输入第二个一元多项式的项数:";cin >> n2;if (n2 >= 1000) {cout << "项数过多,请重新输入:";cin >> n2;}cout << "请输入每一项的系数:" << endl;for (int i = 0;i < n2;i++) {cin >> xs2[i];}cout << "请输入对应项数的次数:" << endl;for (int i = 0;i < n2;i++) {cin >> cs2[i];}cout << "请输入你要进行的运算('+','-','*','>'):" << endl;cin >> x;
}/*
目的:按格式输出结果;
输入参数:结果链表头节点;
返回值;无;
*/
void output(term* p) {int flag1 = 0, flag2 = 0;p = p->next;cout << "结果为:" << endl;while (p != NULL) {if (p->a != 0) {flag2 = 1;}else {p = p->next;continue;}if (p->b <T) {cout << p->a;flag1 = 1;}else {if (flag1 == 0) {if (p->a -1<T && p->b - 1>T)cout << "x^" << p->b;else if (p->a - 1<T && p->b - 1<T)cout << "x";else if (p->a - 1>T && p->b- 1<T)cout << p->a << "x";elsecout << p->a << "x^" << p->b;flag1 = 1;}else {if (p->a - 1<T && p->b - 1>T)cout << "+" << "x^" << p->b;else if (p->a-1<T && p->b - 1<T)cout << "+" << "x";else if (p->a - 1>T && p->b - 1<T)cout << p->a << "x";elsecout << "+" << p->a << "x^" << p->b;}}p = p->next;}if (flag2 == 0)cout << 0 << endl;cout << endl << endl << "----------------------------------" << endl;
}三、总结
老师评价:
1.作为一个计算器而言,输入界面还不够直观,用户体验感缺乏。
2. 输入需要先输入项数,不能直接输入次数和项数。
3.两个一元多项式计算完再计算其他运算需要再次输入次数和系数。
4.基本功能实现,额外实现乘法。
自我体会:
应该将这个当成一个项目,而不是一次题目,应该制造一个人能用的计算器,而不是完成题目给定的要求。