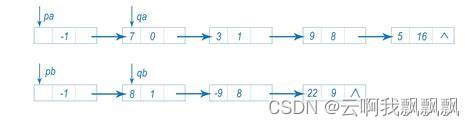
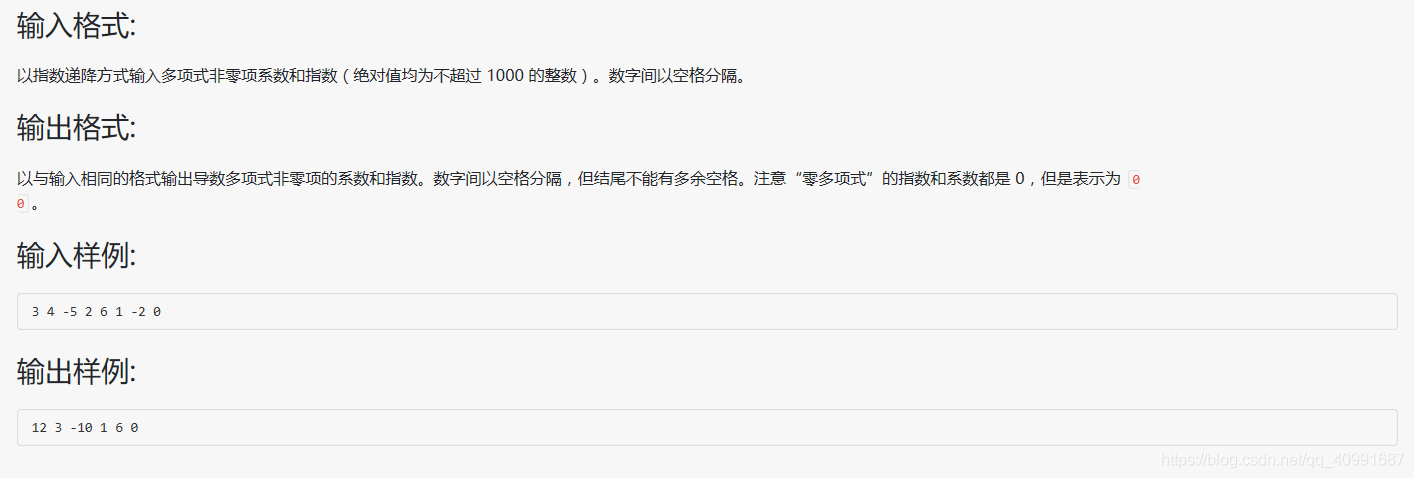
实验内容：把任意给定的两个一元多项式P(x) ,Q(x) 输入计算机，计算它们的和并输出计算结果。

     一元多项式可以用单链表表示，结点结构图示如下：

 

coef

exp

next

       

首先分析一下这个过程是如何实现的

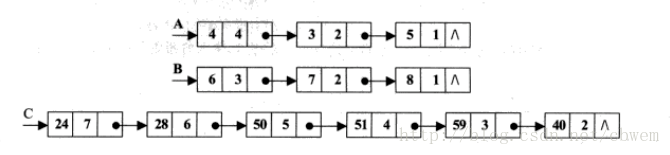
        该算法需要求A与B两个一元多项式的和，那么需要准备三个带头结点的单链表，首先从键盘依次输入A与B一元多项式各项的系数与指数，分别存入两个链表，接着搞个嵌套循环，外循环为A链表，内循环为B链表，功能为从A链表的第一个Node开始去遍历B链表的所有Node，如果有指数相等的Node，那么就将系数相加，存入一个新Node，使第三个链表指向新Node，紧接着删除被加过的Node，根据这个逻辑循环下来，我们可以得到一个求和过的第三个链表，求和完成。

        根据我编写算法过程中，有个需要特别注意的点：删除Node要搞清楚当前删除的是哪个Node，比如链表1->2->3,调用delete（SqList，2）,即1->3,然后再调用一次delete（SqList，2），即1->NULL,这个点非常重要！在我编写算法过程中使我最困扰的一个问题，特别是在循环嵌套中使用这种方法没搞清楚时，难以排查错误！

程序代码

#include <stdio.h>
#include <malloc.h>
#include <stdlib.h>
typedef int DataType;//结点
typedef struct LNode {DataType coef;//系数DataType exp;//指数LNode *next;
} LNode, *LinkList;void getEle(LinkList L) {LinkList p;p = L->next;while(p) {if((p->coef)<0) {printf("-");} else {printf("+");}printf("%dx^%d",abs(p->coef),p->exp);p = p->next;}
}LinkList createList() {int coef;int exp;LinkList headNode;headNode = (LinkList)malloc(sizeof(LNode));int flag = 1;LinkList last = headNode;while(true) {printf("请输入式第%d个系数和指数,(输入404停止插入数据进链表):",flag);scanf("%d %d",&coef,&exp);if(coef == 404 || exp == 404) {break;}LinkList Node = (LinkList)malloc(sizeof(LNode));Node->coef = coef;Node->exp = exp;Node->next = NULL;last->next = Node;last = Node;flag++;}return headNode;
}//删除L链表中的第i个结点
void deleteElem(LinkList L, int i) {int j = 1;LinkList p,q;p = L;while(p->next && j < i) {p = p->next;//第i-1个结点j++;}q = p->next;//第i个结点p->next = q->next;free(q);
}LinkList getSum(LinkList LA, LinkList LB) {LinkList PA = LA->next;LinkList PB = LB->next;LinkList PSum = (LinkList)malloc(sizeof(LNode));//创建头节点LinkList p = PSum;p->next = NULL;int AFlag = 1;int BFlag = 1;while(PA) {PB = LB->next;BFlag = 1;
//		printf("\nA=%d",AFlag);while(PB) {//如果LA表和LB表指数相同,系数相加,并把相加结果放进新Node if(PA->exp == PB->exp) {LinkList q = (LinkList)malloc(sizeof(LNode));q->coef = (PA->coef) + (PB->coef);q->exp = PA->exp;q->next = NULL;p->next = q;p = q;deleteElem(LA,AFlag);PA = LA->next;deleteElem(LB,BFlag);PB = LB->next;//如果LA表和LB表指数不相同,把LA和LB分别放进两个新Node}else{LinkList q1 = (LinkList)malloc(sizeof(LNode));LinkList q2 = (LinkList)malloc(sizeof(LNode));q1->coef = PA->coef;q1->exp = PA->exp;q1->next = q2;q2->coef = PB->coef;q2->exp = PB->exp;q2->next = NULL;p->next = q1;p = q2;deleteElem(LA,AFlag);PA = LA->next;deleteElem(LB,BFlag);PB = LB->next;}
//			PB = PB->next;
//			printf("\nB=%d",BFlag);
//			BFlag++;}
//		PA = PA->next;
//		AFlag++;}getEle(LA);getEle(LB);return PSum;
}int main() {printf("请输入A式\n");LinkList AHead = createList();printf("\n请输入B式\n");LinkList BHead = createList();
//	getEle(AHead);
//	deleteElem(AHead, 2);
//	getEle(AHead);
//	getEle(BHead);printf("\nA和B一元多项式的和为:");LinkList sum = getSum(AHead, BHead);getEle(sum);printf("\n\nauthor by 2062011002-吴奇\n");return 0;
}

 

 实验结果与分析

1. 输入A一元多项式，可以看到有负数也有正数
2. 输入B一元多项式，可以看到有与A式不同的指数
3. 最后得出正确结果

        该算法难度不高，核心内容为A与B求和，如在链表层面无法理解，不妨自行用两个数组去做个小实验：将A数组中的i索引中的值与B数组中的i索引中的值求和放进C数组，这一层面弄清楚之后，这个核心问题将不攻自破

总结

1. 根据我编写算法过程中，有个需要特别注意的点：删除Node要搞清楚当前删除的是哪个Node，比如链表1->2->3,调用delete（SqList，2）,即1->3,然后再调用一次delete（SqList，2），即1->NULL,这个点非常重要！在我编写算法过程中使我最困扰的一个问题，特别是在循环嵌套中使用这种方法没搞清楚时，难以排查错误！
2. 除了其他方法，其中getSum（）方法时间复杂度O（n2），感觉其中并没有改进余地，单链表也无法使用二分查找法，只可只用传统的遍历方法，假如这里我们用到了双向链表不知可否能用二分法。
3. 其次我还认为输入方式不够优雅大气，其实可以将输入方式做一个字符串解析，去判断每一项之前是“+”还是“-”，将该项的系数与指数存入Node，只需在该算法的基础上修改一下输入方式解析一下即可，程序无需大改，但由于本人目前还在投入大量时间学习Java与英语，所以这一步暂时还未实现。
4. 算法总体难度不高，搞懂结构体，面向结构体去编程，这里形似Java面向对象，把每个结构体看作一个类，里面有许多参数，把思维转变成面向对象的想法来编写算法，就是一个大进步！