用单链表实现一元多项式相加

#include<stdio.h>
#include<stdlib.h>
typedef struct Node{float coef;//系数 int exp;//项数 struct Node *next;
}LNode,*Linklist;void newPolynomial(Linklist &head){LNode *p;int i,tempExp;float tempCoef;scanf("%f%d",&tempCoef,&tempExp);head=(struct Node*)malloc(sizeof(struct Node));head->next=NULL;while(tempCoef!=0){  //当系数为0的时候停止录入数据p=(struct Node*)malloc(sizeof(struct Node));p->coef=tempCoef;p->exp=tempExp;p->next=head->next;head->next=p;scanf("%f%d",&tempCoef,&tempExp);}
}void addupPolynomial(Linklist &p1,Linklist &p2,Linklist &sum){Linklist temp1,temp2,tempSum;sum=(struct Node*)malloc(sizeof(struct Node));sum->next=NULL;//新多项式的头结点 temp1=p1->next;temp2=p2->next;while(temp1!=NULL&&temp2!=NULL){    //当p1,p2多项式都没遍历完 tempSum=(struct Node*)malloc(sizeof(struct Node));if(temp1->exp==temp2->exp){tempSum->exp=temp1->exp;tempSum->coef=temp1->coef+temp2->coef;tempSum->next=sum->next;sum->next=tempSum;temp1=temp1->next;temp2=temp2->next;}else if(temp1->exp<temp2->exp){tempSum->exp=temp1->exp;tempSum->coef=temp1->coef;tempSum->next=sum->next;sum->next=tempSum;temp1=temp1->next;}else{tempSum->exp=temp2->exp;tempSum->coef=temp2->coef;tempSum->next=sum->next;sum->next=tempSum;temp2=temp2->next;}}while(temp1!=NULL){//当p1没遍历完 tempSum=(struct Node*)malloc(sizeof(struct Node));tempSum->exp=temp1->exp;tempSum->coef=temp1->coef;tempSum->next=sum->next;sum->next=tempSum;temp1=temp1->next;}while(temp2!=NULL){//当p2没遍历完 tempSum=(struct Node*)malloc(sizeof(struct Node));tempSum->exp=temp2->exp;tempSum->coef=temp2->coef;tempSum->next=sum->next;sum->next=tempSum;temp2=temp2->next;}
}void bubbleSort(Linklist &head){ //冒泡排序 Linklist p,q,tail;tail = NULL;while((head->next->next) != tail){p = head;q = head->next;while(q->next != tail){if((q->exp) > (q->next->exp)){p->next = q->next;q->next = q->next->next;p->next->next = q;q = p->next;}q = q->next;p = p->next;}tail = q;}
}void printPolynomial(Linklist &head){Linklist temp;temp=head;printf("多项式为：");while(temp->next!=NULL){temp=temp->next;if(temp->next!=NULL){printf("%.1fx^%d+",temp->coef,temp->exp);}else{printf("%.1fx^%d",temp->coef,temp->exp);}}
}void newPolynomial(Linklist &head);
void addupPolynomial(Linklist &p1,Linklist &p2,Linklist &sum);
void bubbleSort(Linklist &head);
void printPolynomial(Linklist &head);int main()
{	Linklist L1,L2,sumL; printf("\n**************请输入第一个多项式***************\n");newPolynomial(L1);bubbleSort(L1);printPolynomial(L1);printf("\n**************请输入第二个多项式***************\n");newPolynomial(L2);bubbleSort(L2);printPolynomial(L2);addupPolynomial(L1,L2,sumL);bubbleSort(sumL);printf("\n相加的多项式为:");printPolynomial(sumL);
} 

算法的核心思想是，
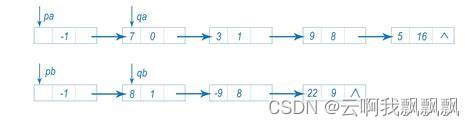
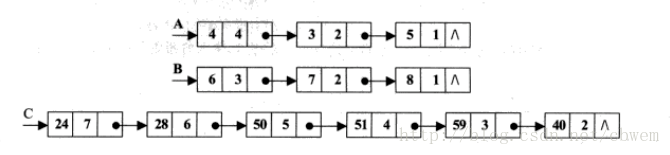
先把输入的多项式，按次数从小到大排序，然后用temp1，temp2同时分别遍历两个多项式，

当temp1所指结点的次数小于temp2所指结点，取temp1所指结点作为新多项式的新项，
同时temp1前进一个节点，temp2不动；
当temp1所指结点的次数大于temp2所指结点，取temp2所指结点作为新多项式的新项，
同时temp2前进一个节点，temp1不动；
当temp1所指结点的次数等于temp2所指结点的次数，取temp1所指结点和temp2所指结点之和作为新多项式的新项，此时temp1，temp2都前进一个结点。

注意，排序是必不可少的一步
这里的排序方法采用的是冒泡排序，不懂的同鞋可以自行百度学习；