1、实现方式:可采用线性表的顺序存储结构,但是当多项式的每个项的指数差别很大时,会浪费很多存储空间。所以采用链式存储方式表示,每一项可以表示成一个结点,结点的结构由存放系数的coef域,存放指数的expn域和指向下一个结点的next指针域组成。
2、链表结构:


3、一元多项式的加法运算:
设La和Lb分别表示两个多项式。Lc表示和多项式。p,q,r分别表示指向单链表的当前项比较指数大小。
(1)若La->expn < Lb->expn,则结点p应是和多项式中的一项,将p复制到r,并使p后移。
(2)若La->expn = Lb->exp ,则将两个结点中的系数相加,当和不为0时,La的系数域加上Lb的系数域作为Lc的系数域;若和为0,则和多项式中没有这一项,p,q后移。
(3)若La->exp > Lb->exp ,则将结点q复制到Lc中,q后移。
//多项式相加,po1 += po2
bool Add(Poly po1,Poly po2)
{PNode *p = po1->next; //p指向po1的第一个节点PNode *q = po2->next; //q指向po2的第一个节点PNode *pre = po1;PNode *temp;while(p != NULL && q != NULL) //当两个多项式均未扫描结束时{if(p->expn < q->expn) //如果p指向的多项式的指数小于q的指数,将p节点加入到和多项式中{pre->next = p; //将p节点加入到pre中pre = p; //p即为现在的pre节点p = p->next; //继续判断p的下一个节点}else if(p->expn > q->expn) //将节点q插入到节点p之前,指针q指向原节点的下一个节点{pre->next = q; //将q节点加入到和多项式中pre = q; //q即为现在的pre节点q = q->next; //继续判断q的下一个节点}else if(p->expn == q->expn) //若指数相同,则相应的系数相加{p->cofe += q->cofe;if(po1->cofe == 0) //若系数和为0,则删除节点p与q,并将指针指向下一个节点{temp = p->next; free(p); //删除节点pp = temp; //使指针p指向它原节点的下一个节点temp = q->next;free(q); //删除节点qq = temp; //使指针q指向它原节点的下一个节点}else{pre->next = p; //由于将两个多项式的和存储到p,所以将p加入到pre中pre = p;p = p->next;temp = q->next;free(q); //将po2链中相应项释放掉,和放到po1链中q = temp;}}}//若多项式中还有剩余,则将剩余的节点加入到和多项式中pre->next = p ? p : q;return true;
}4、一元多项式的减法运算:
算法:将减数多项式的所有系数先变为相反数,然后调用多项式相加的函数进行运算。
//多项式相减,po1 -= po2
bool Sub(Poly po1,Poly po2) //相减就是先将减数中每一项的系数变为负,再将两个多项式相加
{PNode *p = po1->next; //p指向po1的第一个节点PNode *q = po2->next; //q指向po2的第一个节点PNode *pre = po1;PNode *temp;while(q->next != NULL) //将q中的每一项的系数变为负{q->cofe = 0 - q->cofe;q = q->next;}q = po2->next; //上一个循环将q指向最后一个节点,现在重新使q变成po2->nextwhile(p != NULL && q != NULL) //当两个多项式均未扫描结束时{if(p->expn < q->expn) //如果p指向的多项式的指数小于q的指数,将p节点加入到和多项式中{pre->next = p; //将p节点加入到pre中pre = p; //p即为现在的pre节点p = p->next; //继续判断p的下一个节点}else if(p->expn > q->expn) //将节点q插入到节点p之前,指针q指向原节点的下一个节点{pre->next = q; //将q节点加入到和多项式中pre = q; //q即为现在的pre节点q = q->next; //继续判断q的下一个节点}else if(p->expn == q->expn) //若指数相同,则相应的系数相加{p->cofe += q->cofe;if(po1->cofe == 0) //若系数和为0,则删除节点p与q,并将指针指向下一个节点{temp = p->next; free(p); //删除节点pp = temp; //使指针p指向它原节点的下一个节点temp = q->next;free(q); //删除节点qq = temp; //使指针q指向它原节点的下一个节点}else{pre->next = p; //由于将两个多项式的和存储到p,所以将p加入到pre中pre = p;p = p->next;temp = q->next;free(q); //将po2链中相应项释放掉,和放到po1链中q = temp;}}}//若多项式中还有剩余,则将剩余的节点加入到和多项式中pre->next = p ? p : q;return true;
}5、一元多项式的乘法运算:
两个一元多项式的相乘运算,需要将一个多项式的每一项的指数与另一个多项式的每一项的指数相加,并将其系数相乘。
例如两个多项式A(x)和B(x)相乘后得到C(x)。A(x)=4x4+3x2+5x,B(x)=6x3+7x2+8x,C(x)=24x7+28x6+50x5+51x4+59x3+40x2表示成链式存储结构如下图所示。
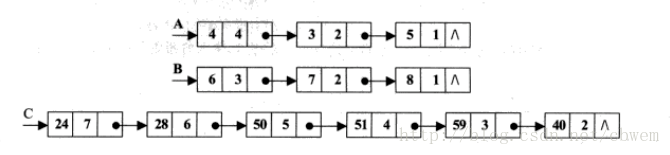
算法思想:设A、B和C分别是多项式A(x)、B(x)和C(x)对应链表的头指针,要计算出A(x)和B(x)的最高指数和,即4+3=7,则A(x)和B(x)的乘机C(x)的指数范围在0~7之间。然后将A(x)的各项按照指数降幂排列,将B(x)按照指数升幂排列,分别设两个指针pa和pb,pa用来指向链表A,pb用来指向链表B,从第一个结点开始计算两个链表的expn域的和,并将其与k比较(k为指数和的范围,从7到0递减),使链表的和呈递减排列。若和小于k,则pb=pb->next;若和等于k,则求出两个多项式系数的乘积,并将其存入新结点中。若和大于k,则pa=pa->next。这样就可以得到多项式 A(x)和B(x)的乘积C(x)。算法结束后重新将链表B逆置,将其恢复原样。
PNode *Reverse(Poly pl) //链表逆置,使一元多项式呈指数递增形式
{assert(pl != NULL);if(pl == NULL){return false;}PNode *q = pl->next;PNode *p = NULL;PNode *tmp;while(q){tmp = q->next; //tmp指向链表的待处理节点q->next = p; //将链表节点逆置p = q; //p指向刚逆置后链表节点q = tmp; //q指向下一准备逆置的节点}pl->next = p; //将头结点的指针指向已经逆置后的节点return pl;
}//多项式相乘,po1 *= po2
//相乘前,A,B两个多项式均是升幂排序
//相乘时,A为降幂排序,B为升幂排序
PNode *Mutil(Poly po1,Poly po2) //两个多项式相乘,应该是第一个多项式中的每一项分别与第二个多项式相乘,将相乘得到的结果都存在第一个多项式中,再调用合并多项式的函数
{PNode *p1,*p2,*tmp,*ne,*head; int k,maxExpn,minExpn;float coef; //总的指数和head = (PNode *)malloc(sizeof(PNode));//头结点 head->next = NULL;if(po1->next !=NULL && po2->next != NULL){minExpn = po1->next->expn + po2->next->expn; //minExpn为两个多项式中指数和的最小值 Reverse(po1); //将A降幂排列 Reverse(po2); //将B降幂排列 maxExpn = po1->next->expn + po2->next->expn; //maxExpn为两个多项式中指数和的最大值}else{ return head;} tmp = head;Reverse(po2); //将po2升幂排列 for(k = maxExpn;k >= minExpn;k--){ //多项式的乘积指数范围为:minExpn~maxExpn//根据两项的指数和使每一次循环都得到新多项式中一项 p1 = po1->next;while(p1 !=NULL && p1->expn > k){ //找到p1的位置 p1 = p1->next;}p2 = po2->next;while(p2!=NULL && p1!=NULL && p1->expn + p2->expn < k){ //如果指数和和小于k,pb后移结点 p2 = p2->next;} coef=0.0; while(p1!=NULL && p2!=NULL) { if(p1->expn + p2->expn == k) { //如果指数和等于k,系数和累加,且pa,pb均后移结点 coef += p1->cofe *p2->cofe; p1 = p1->next; p2 = p2->next; } else if(p1->expn + p2->expn > k) { //如果指数和大于k,pb后移结点 p1 = p1->next; } else { //如果指数和和小于k,pb后移结点 p2 = p2->next; } } if(coef!=0.0) {//如果系数和不为0,则生成新结点,将系数和指数赋给新结点后插入到新多项式中 ne = (PNode *)malloc(sizeof(PNode)); ne->cofe = coef; ne->expn = k; ne->next = tmp->next; tmp->next = ne; tmp = ne; } } Reverse(po2); Reverse(head); return head; //返回新多项式的头结点
}6、完整代码实现:
(1)poly.h:
//利用带头节点的单链表表示一元多项式
#pragma oncetypedef struct PNode
{double cofe;//系数int expn;//指数struct PNode *next;
}PNode,*Poly;//void InitPoly(Poly po);//按指数升序排列
bool Insert(Poly po,double cofe,int expn);void Show(Poly po);//多项式相加,po1 += po2
bool Add(Poly po1,Poly po2);//多项式相减,po1 -= po2
bool Sub(Poly po1,Poly po2);//单链表逆置
PNode *Reverse(Poly pl);//多项式相乘,po1 *= po2
PNode *Mutil(Poly po1,Poly po2);(2)poly.cpp:
//利用带头节点的单链表表示一元多项式
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include "poly.h"void InitPoly(Poly po)
{po->next = NULL;
}//查找这个数应该存放的位置
static PNode *Search(Poly po,int expn)
{PNode *p;for(p = po;p->next != NULL;p = p->next){if(p->next->expn >= expn){return p;}}return p;
}//按指数升序排列
bool Insert(Poly po,double cofe,int expn)
{PNode *p = Search(po,expn);PNode *q = p->next;//如果该节点存在,则合并同类项if(p->next != NULL && p->next->expn == expn) //合并同类项{q->cofe += cofe;if(-0.00001<q->cofe && q->cofe<0.00001) //系数为0{p->next = q->next;free(q);}}//不存在,则创建新的节点else //创建新节点{q = (PNode *)malloc(sizeof(PNode));q->cofe = cofe;q->expn = expn;q->next = p->next;p->next = q;}return true;
}void Show(Poly po)
{PNode *p = po->next;while(p){printf("%1.1f",p->cofe);if(p->expn){printf("*x^%d",p->expn);}if(p->next&&p->next->cofe>0){printf("+");}p=p->next;}printf("\n");
}//多项式相加,po1 += po2
bool Add(Poly po1,Poly po2)
{PNode *p = po1->next; //p指向po1的第一个节点PNode *q = po2->next; //q指向po2的第一个节点PNode *pre = po1;PNode *temp;while(p != NULL && q != NULL) //当两个多项式均未扫描结束时{if(p->expn < q->expn) //如果p指向的多项式的指数小于q的指数,将p节点加入到和多项式中{pre->next = p; //将p节点加入到pre中pre = p; //p即为现在的pre节点p = p->next; //继续判断p的下一个节点}else if(p->expn > q->expn) //将节点q插入到节点p之前,指针q指向原节点的下一个节点{pre->next = q; //将q节点加入到和多项式中pre = q; //q即为现在的pre节点q = q->next; //继续判断q的下一个节点}else if(p->expn == q->expn) //若指数相同,则相应的系数相加{p->cofe += q->cofe;if(po1->cofe == 0) //若系数和为0,则删除节点p与q,并将指针指向下一个节点{temp = p->next; free(p); //删除节点pp = temp; //使指针p指向它原节点的下一个节点temp = q->next;free(q); //删除节点qq = temp; //使指针q指向它原节点的下一个节点}else{pre->next = p; //由于将两个多项式的和存储到p,所以将p加入到pre中pre = p;p = p->next;temp = q->next;free(q); //将po2链中相应项释放掉,和放到po1链中q = temp;}}}//若多项式中还有剩余,则将剩余的节点加入到和多项式中pre->next = p ? p : q;return true;
}//多项式相减,po1 -= po2
bool Sub(Poly po1,Poly po2) //相减就是先将减数中每一项的系数变为负,再将两个多项式相加
{PNode *p = po1->next; //p指向po1的第一个节点PNode *q = po2->next; //q指向po2的第一个节点PNode *pre = po1;PNode *temp;while(q->next != NULL) //将q中的每一项的系数变为负{q->cofe = 0 - q->cofe;q = q->next;}q = po2->next; //上一个循环将q指向最后一个节点,现在重新使q变成po2->nextwhile(p != NULL && q != NULL) //当两个多项式均未扫描结束时{if(p->expn < q->expn) //如果p指向的多项式的指数小于q的指数,将p节点加入到和多项式中{pre->next = p; //将p节点加入到pre中pre = p; //p即为现在的pre节点p = p->next; //继续判断p的下一个节点}else if(p->expn > q->expn) //将节点q插入到节点p之前,指针q指向原节点的下一个节点{pre->next = q; //将q节点加入到和多项式中pre = q; //q即为现在的pre节点q = q->next; //继续判断q的下一个节点}else if(p->expn == q->expn) //若指数相同,则相应的系数相加{p->cofe += q->cofe;if(po1->cofe == 0) //若系数和为0,则删除节点p与q,并将指针指向下一个节点{temp = p->next; free(p); //删除节点pp = temp; //使指针p指向它原节点的下一个节点temp = q->next;free(q); //删除节点qq = temp; //使指针q指向它原节点的下一个节点}else{pre->next = p; //由于将两个多项式的和存储到p,所以将p加入到pre中pre = p;p = p->next;temp = q->next;free(q); //将po2链中相应项释放掉,和放到po1链中q = temp;}}}//若多项式中还有剩余,则将剩余的节点加入到和多项式中pre->next = p ? p : q;return true;
}PNode *Reverse(Poly pl) //链表逆置,使一元多项式呈指数递增形式
{assert(pl != NULL);if(pl == NULL){return false;}PNode *q = pl->next;PNode *p = NULL;PNode *tmp;while(q){tmp = q->next; //tmp指向链表的待处理节点q->next = p; //将链表节点逆置p = q; //p指向刚逆置后链表节点q = tmp; //q指向下一准备逆置的节点}pl->next = p; //将头结点的指针指向已经逆置后的节点return pl;
}//多项式相乘,po1 *= po2
//相乘前,A,B两个多项式均是升幂排序
//相乘时,A为降幂排序,B为升幂排序
PNode *Mutil(Poly po1,Poly po2) //两个多项式相乘,应该是第一个多项式中的每一项分别与第二个多项式相乘,将相乘得到的结果都存在第一个多项式中,再调用合并多项式的函数
{PNode *p1,*p2,*tmp,*ne,*head; int k,maxExpn,minExpn;float coef; //总的指数和head = (PNode *)malloc(sizeof(PNode));//头结点 head->next = NULL;if(po1->next !=NULL && po2->next != NULL){minExpn = po1->next->expn + po2->next->expn; //minExpn为两个多项式中指数和的最小值 Reverse(po1); //将A降幂排列 Reverse(po2); //将B降幂排列 maxExpn = po1->next->expn + po2->next->expn; //maxExpn为两个多项式中指数和的最大值}else{ return head;} tmp = head;Reverse(po2); //将po2升幂排列 for(k = maxExpn;k >= minExpn;k--){ //多项式的乘积指数范围为:minExpn~maxExpn//根据两项的指数和使每一次循环都得到新多项式中一项 p1 = po1->next;while(p1 !=NULL && p1->expn > k){ //找到p1的位置 p1 = p1->next;}p2 = po2->next;while(p2!=NULL && p1!=NULL && p1->expn + p2->expn < k){ //如果指数和和小于k,pb后移结点 p2 = p2->next;} coef=0.0; while(p1!=NULL && p2!=NULL) { if(p1->expn + p2->expn == k) { //如果指数和等于k,系数和累加,且pa,pb均后移结点 coef += p1->cofe *p2->cofe; p1 = p1->next; p2 = p2->next; } else if(p1->expn + p2->expn > k) { //如果指数和大于k,pb后移结点 p1 = p1->next; } else { //如果指数和和小于k,pb后移结点 p2 = p2->next; } } if(coef!=0.0) {//如果系数和不为0,则生成新结点,将系数和指数赋给新结点后插入到新多项式中 ne = (PNode *)malloc(sizeof(PNode)); ne->cofe = coef; ne->expn = k; ne->next = tmp->next; tmp->next = ne; tmp = ne; } } Reverse(po2); Reverse(head); return head; //返回新多项式的头结点
}(3)main.cpp:
#include <stdio.h>
#include "poly.h"int main()
{PNode po1;InitPoly(&po1);Insert(&po1,1,1);Insert(&po1,2,2);Insert(&po1,5,5);Insert(&po1,3,0);Insert(&po1,6,2);Insert(&po1,-5,5);Show(&po1);PNode po2;InitPoly(&po2);Insert(&po2,1,1);Insert(&po2,2,2);Insert(&po2,5,5);Insert(&po2,3,0);Insert(&po2,6,2);Insert(&po2,-5,5);Insert(&po2,5,3);Insert(&po2,3,1);Insert(&po2,6,2);Show(&po2);PNode *p = Mutil(&po1,&po2);Show(p);//Add(&po1,&po2);//Show(&po1);//Sub(&po1,&po2);//Show(&po1);return 0;
}