熟悉 vue 和 react 的小伙伴们都知道,在执行过程中会有各种生命周期钩子,其实webpack也不例外,在使用webpack的时候,我们有时候需要在 webpack 构建流程中引入自定义的行为,这个时候就可以在 hooks 钩子中添加自己的方法。
创建插件
webpack 加载 webpack.config.js 中所有配置,此时 webpack 创建 compiler 对象,遍历所有 plugins 中插件,调用插件的 apply 方法,执行剩下编译流程(触发各个 hooks 事件),具体使用什么钩子和钩子是同步还是异步,请移步compiler 钩子
- 创建一个 JavaScript 命名函数或 JavaScript 类
- 在插件函数的 prototype 上定义一个 apply 方法
- 绑定到 webpack 自身的事件钩子上
- 导出这个JavaScript 命名函数或 JavaScript 类
- 在 webpack.config.js 文件中引入并调用方法
自定义 banner-webpack-plugin
自定义 banner-webpack-plugin 插件,该插件会在每一个打包后的 js 、css 文件第一行添加注释,先看效果图。

- emit 钩子是输出 asset 到 output 目录之前执行
- 获取即将输出的资源文件:compilation.assets
- 遍历 assets,只处理js和css资源,其他文件不处理
- 通过 content = entcompilation.assets[filename].source() 获取原来内容
- 拼接上注释 content = prefix + content
- 修改资源的 source 和 size
// plugins/banner-webpack-plugin.jsclass BannerWebpackPlugin {constructor(options = {}) {this.options = options;}apply(compiler) {// 在资源输出之前触发compiler.hooks.emit.tap("BannerWebpackPlugin", (compilation) => {const extensions = ["css", "js"];const prefix = `/** Author: ${this.options.author}* Build Time: ${new Date()}*/`;// 获取即将输出的资源文件:compilation.assetsfor (const filename in compilation.assets) {if (compilation.assets.hasOwnProperty(filename)) {// 将文件名进行切割const splitted = filename.split(".");// 获取文件扩展名const extension = splitted[splitted.length - 1];// 只处理js和css资源,其他文件不处理if (extensions.includes(extension)) {const asset = compilation.assets[filename];// 获取原来内容let content = asset.source();// 拼接上注释content = prefix + content;// 修改资源compilation.assets[filename] = {// 最终资源输出时,调用source方法,source方法的返回值就是资源的具体内容source: () => content,// 资源大小size: () => content.length,};}}}});}
}
module.exports = BannerWebpackPlugin;
调用 BannerWebpackPlugin
// config/webpack.config.js// 引入插件
const BannerWebpackPlugin = require('../plugins/banner-webpack-plugin');
module.exports = {plugins: [// 调用插件new BannerWebpackPlugin({author: "小小愿望",}),],
};
自定义 take-time-webpack-plugin
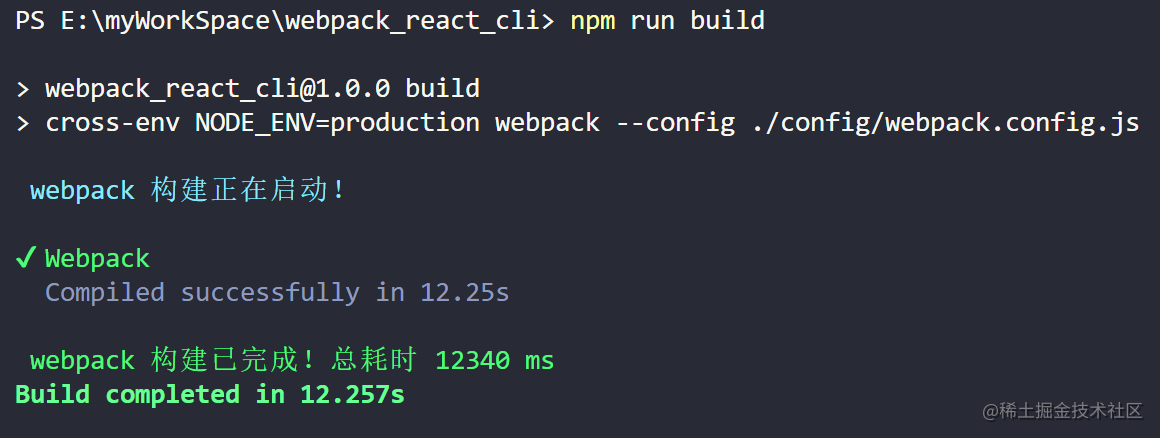
自定义 take-time-webpack-plugin 插件,该插件输出 “webpack 构建正在启动!”,打包完成后输出 webpack 构建已完成!总耗时 { time } ms,先看效果图。
// plugins/take-time-webpack-plugin.js// 一个命名的 Javascript 方法 或 JavaScript 类
class TakeTimeWebpackPlugin {time = 0;// 原型上需要定义 apply 的方法apply(compiler) {// 生命周期钩子函数,是由 compiler 暴露// 通过 compiler 获取 webpack 内部的钩子,获取 Webpack 打包过程中的各个阶段compiler.hooks.environment.tap("TakeTimeWebpackPlugin", (compilation) => {console.log("\x1B[36m", "webpack 构建正在启动!");this.time = new Date().getTime();});// 通过 compiler 获取 webpack 内部的钩子,获取 Webpack 打包过程中的各个阶段compiler.hooks.afterEmit.tapAsync("TakeTimeWebpackPlugin", (compilation, callback) => {const nowTime = new Date().getTime();this.time = nowTime - this.time;const str = `webpack 构建已完成!总耗时 ${this.time} ms`console.log("\x1B[32m", str);// 分为同步和异步的钩子,异步钩子在功能完成后,必须执行对应的回调callback();});}
}
module.exports = TakeTimeWebpackPlugin;
调用 TakeTimeWebpackPlugin
在 config/webpack.config.js 文件中引入并执行 TakeTimeWebpackPlugin
// config/webpack.config.js// 引入插件
const TakeTimeWebpackPlugin = require('../plugins/take-time-webpack-plugin');
module.exports = {plugins: [// 调用插件new TakeTimeWebpackPlugin(),],
};