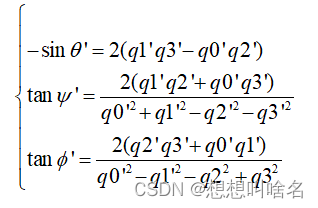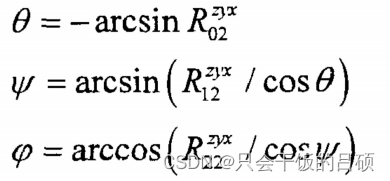欧拉角、旋转矩阵及四元数
- 1. 简介
- 2. 欧拉角
- 2.1 欧拉角定义
- 2.2 右手系和左手系
- 2.3 转换流程
- 3. 旋转矩阵
- 4. 四元数
- 4.1 四元数与欧拉角和旋转矩阵之间等效变换
- 4.2 测试Matlab代码
- 5. 总结
1. 简介
常用姿态参数表达方式包括方向余弦矩阵、欧拉轴/角参数、欧拉角、四元数以及罗德里格参数等。高分辨率光学遥感卫星主要采用欧拉角与四元数对姿态参数进行描述。这里着重讲解欧拉角、旋转矩阵和四元数。
2. 欧拉角
2.1 欧拉角定义
欧拉角是表征刚体旋转的一种方法之一,由莱昂哈德·欧拉 引入的三个角度,用于描述刚体相对于固定坐标系的方向。在摄影测量、空间科学或其它技术领域,一般用一组(三个)欧拉角描述两个空间坐标之间的旋转变换关系。
刚体在三维空间的一次旋转可以由绕 X \mathrm{X} X 轴旋转的角度、绕 Y \mathrm{Y} Y 轴旋转的角度、绕 Z \mathrm{Z} Z 轴旋转的角度来表征, 这三个角度分别是横滚角(roll, 符号 φ \varphi φ )、俯仰角(pitch, 符号 θ \theta θ )、航向角(yaw, 符号 ψ \psi ψ ),或者用符号 α \alpha α、 β \beta β和 γ \gamma γ分别表示绕XYZ轴(横滚、俯仰和航向)旋转的角度。 三个角的正负号可由右手定则表示。

相比于其它姿态参数表达方式,欧拉角参数具有明显的几何意义,可以更加直接对姿态动力学方程进行描述。根据欧拉定理得到,刚体绕固定点的位移可以转成若干次有限转动的合成。针对高分辨率光学遥感卫星,同样可以采用上述原理与方法实现参考坐标系(J2000坐标系、WGS84坐标系)与卫星本体坐标系之间转换。参考坐标系与本体坐标系间转换过程中,不同的转动顺序与方式将会得到不同形式的欧拉角参数。
2.2 右手系和左手系

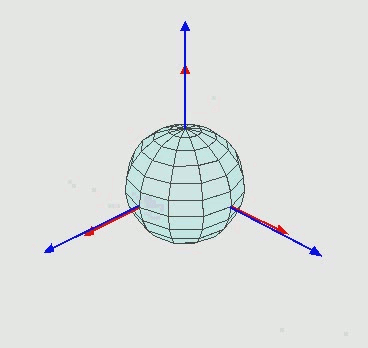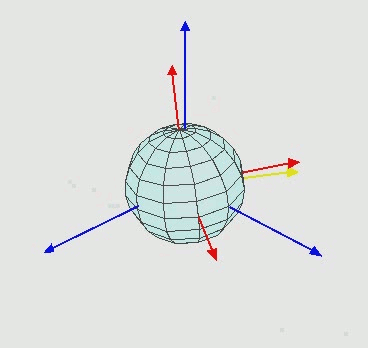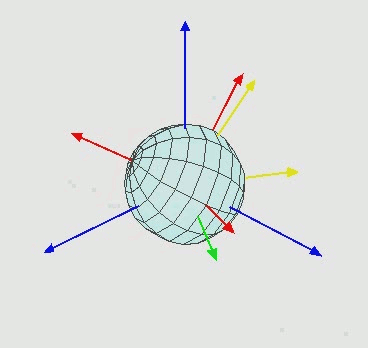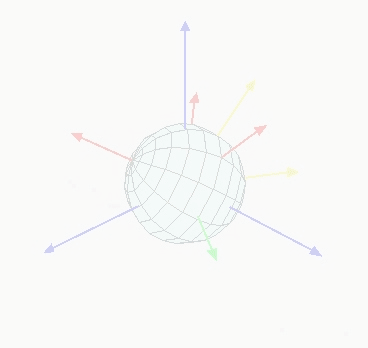
左图和右图分别是左手系和右手系。
对于右手坐标,右拇指沿 z 轴指向正方向,食指指向x 轴,中指指向y轴。
对于左手坐标,左拇指沿 z 轴指向正方向,食指指向x 轴,中指指向y轴。
2.3 转换流程
刚体的取向可以用三个基本旋转矩阵来决定。换句话说,任何关于刚体旋转的旋转矩阵是由三个基本旋转矩阵复合而成的 。 由坐标系 S a S_{a} Sa 到 S b S_{b} Sb 的变换可通过以下三次连续的转动实现:

Step1:坐标系 O − x a y a z a O-x_{a} y_{a} z_{a} O−xayaza 绕 z a z_{a} za 轴逆时针转过角 ψ \psi ψ, 称为 O − x ′ y ′ z a O-x^{\prime} y^{\prime} z_{a} O−x′y′za;
Step2:坐标系 O − x ′ y ′ z a O-x^{\prime} y^{\prime} z_{a} O−x′y′za绕 y ′ y' y′ 轴逆时针转过角 θ \theta θ, 称为 O − x b y ′ z ′ ′ O-x_b y^{\prime} z'' O−xby′z′′;
Step3: 坐标系 O − x b y ′ z ′ ′ O-x_{b} y^{\prime} z^{\prime \prime} O−xby′z′′ 绕 x b x_{b} xb 轴逆时针转过角 φ \varphi φ, 称为 O − x b y b z b O-x_{b} y_{b} z_{b} O−xbybzb 。
上述旋转角 φ , θ , ψ \varphi, \theta, \psi φ,θ,ψ 就是一组欧拉角, 它们完全决定 S a S_{a} Sa 到 S b S_{b} Sb 之间的相对姿态, 其中转动过程可用符号表示:
S a ⟶ R z ( ψ ) ∘ ⟶ R y ( θ ) ∘ ⟶ R x ( φ ) S b S_{a} \stackrel{R_{z}(\psi)}{\longrightarrow} \circ \stackrel{R_{y}(\theta)}{\longrightarrow} \circ \stackrel{R_{x}(\varphi)}{\longrightarrow} S_{b} Sa⟶Rz(ψ)∘⟶Ry(θ)∘⟶Rx(φ)Sb
经过三次变换,得到:
[ x b y b z b ] = R x ( φ ) R y ( θ ) R z ( ψ ) [ x a y a z a ] \left[\begin{array}{l} x_{b} \\ y_{b} \\ z_{b} \end{array}\right]=R_{x}(\varphi) R_{y}(\theta) R_{z}(\psi)\left[\begin{array}{l} x_{a} \\ y_{a} \\ z_{a} \end{array}\right] ⎣⎡xbybzb⎦⎤=Rx(φ)Ry(θ)Rz(ψ)⎣⎡xayaza⎦⎤
所以由 S a S_{a} Sa 到 S b S_{b} Sb 的坐标变换矩阵为:
R = R x ( φ ) R y ( θ ) R z ( ψ ) R=R_{x}(\varphi) R_{y}(\theta) R_{z}(\psi) R=Rx(φ)Ry(θ)Rz(ψ)
一般来说, 三维空间的坐标变换可以由三次基元变换矩阵相乘得到。当欧拉角的定义与上述顺序和旋转方向不一致时,仍可按照上述原则处理。使用欧拉角时,我们必须明确表示出夹角的顺序。这三个旋转是依次施加的,顺序不同,产生的结果也不同。因此,使用欧拉角前,必须先做好明确的定义。
旋转顺序: 在经典力学里,时常用yxz顺序来设定欧拉角;照着第二个转动轴的轴名,简称为x顺序。还有一种顺序,xyz顺序,常用在航空航天工程中 。
任何方向都可以通过从已知的标准方向开始组成三个元素旋转来实现。等价地,任何旋转矩阵R都可以分解为三个元素旋转矩阵的乘积。例如:
R = R x ( α ) R y ( β ) R z ( γ ) {\displaystyle R=R_x(\alpha )R_y(\beta )R_z(\gamma )} R=Rx(α)Ry(β)Rz(γ)
或者
R = R x ( φ ) R y ( θ ) R z ( ψ ) {\displaystyle R=R_x(\varphi )R_y(\theta )R_z(\psi )} R=Rx(φ)Ry(θ)Rz(ψ)
滚动角的大小范围为 − π — π -\pi—\pi −π—π 。在围绕 X \mathrm{X} X 轴旋转 φ \varphi φ 之后, 可以用旋转矩阵 R x ( φ ) R_{x}(\varphi) Rx(φ) 表 示, 如下式:
R x ( φ ) = [ 1 0 0 0 cos φ sin φ 0 − sin φ cos φ ] \boldsymbol{R}_{x}(\varphi)=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \varphi & \sin \varphi \\ 0 & -\sin \varphi & \cos \varphi \end{array}\right] Rx(φ)=⎣⎡1000cosφ−sinφ0sinφcosφ⎦⎤
俯仰角的大小在 − π / 2 — π / 2 -\pi / 2—\pi / 2 −π/2—π/2 之间。在绕 Y \mathrm{Y} Y 轴转动 θ \theta θ 之后, 可以用 R y ( θ ) \boldsymbol{R}_{\mathrm{y}}(\theta ) Ry(θ) 来表示:
R y ( θ ) = [ cos θ 0 − sin θ 0 1 0 sin θ 0 cos θ ] \boldsymbol{R}_{y}(\theta)=\left[\begin{array}{ccc} \cos \theta & 0 & -\sin \theta \\ 0 & 1 & 0 \\ \sin \theta & 0 & \cos \theta \end{array}\right] Ry(θ)=⎣⎡cosθ0sinθ010−sinθ0cosθ⎦⎤
航向角的大小范围为 − π — π -\pi—\pi −π—π 。在绕 Z 轴旋转 φ \varphi φ 后, 可以用旋转矩阵 R y ( ψ ) \boldsymbol{R}_{\mathrm{y}}(\psi) Ry(ψ) 来表 示:
R z ( ψ ) = [ cos ψ sin ψ 0 − sin ψ cos ψ 0 0 0 1 ] \boldsymbol{R}_{z}(\psi )=\left[\begin{array}{ccc} \cos \psi & \sin \psi & 0 \\ -\sin \psi & \cos \psi & 0 \\ 0 & 0 & 1 \end{array}\right] Rz(ψ)=⎣⎡cosψ−sinψ0sinψcosψ0001⎦⎤
沿着不同旋转方向的欧拉角会导致旋转矩阵不同, 所以在用欧拉角表征时, 要给出旋转顺序。下图为转换的基元变化:

欧拉角优点和缺点:
(1)三个角度组成,直观,容易理解。可以进行从一个方向到另一个方向旋转大于180度的角度。
(2)对两个朝向进行插值比较困难。简单地对X、Y、Z角度进行插值得到的结果不太理想。
(3)实施多次旋转很复杂且不精确,必须计算出最终的旋转矩阵,然后据此推测出欧拉角。
(4)死锁问题。
参考:四元数与欧拉角
3. 旋转矩阵
参考:旋转矩阵与欧拉角之间的转换。Euler Angle Formulas 给出了不同顺序下测转换矩阵,下面是xyz顺序转换矩阵。其中,cx、cy、cz分别表示绕xyz轴的旋转角余弦,sx、sy、sz分别表示绕xyz轴的旋转角正弦。当旋转顺序为航向角-俯仰角-横滚角时, 其对应的旋转矩阵是按顺序矩阵相乘的结果:
R = R x ( φ ) R y ( θ ) R z ( ψ ) = [ cos θ cos ψ sin ψ cos θ − sin θ − cos ψ sin ψ cos ψ cos φ + sin ψ sin θ sin φ cos θ sin φ sin ψ sin φ + cos ψ sin θ cos φ − cos ψ sin φ + sin ψ sin θ cos φ cos θ cos φ ] = [ R 11 R 12 R 13 R 21 R 22 R 23 R 31 R 32 R 33 ] \begin{aligned} &\boldsymbol{R}=\boldsymbol{R}_{x}(\varphi) \boldsymbol{R}_{y}(\theta) \boldsymbol{R}_{z}(\psi ) \\ &=\left[\begin{array}{ccc} \cos \theta \cos \psi & \sin \psi \cos \theta & -\sin \theta \\ -\cos \psi \sin \psi & \cos \psi \cos \varphi+\sin \psi \sin \theta \sin \varphi & \cos \theta \sin \varphi \\ \sin \psi \sin \varphi+\cos \psi \sin \theta \cos \varphi & -\cos \psi \sin \varphi+\sin \psi \sin \theta \cos \varphi & \cos \theta \cos \varphi \end{array}\right] \\ &=\left[\begin{array}{lll} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{array}\right] \end{aligned} R=Rx(φ)Ry(θ)Rz(ψ)=⎣⎡cosθcosψ−cosψsinψsinψsinφ+cosψsinθcosφsinψcosθcosψcosφ+sinψsinθsinφ−cosψsinφ+sinψsinθcosφ−sinθcosθsinφcosθcosφ⎦⎤=⎣⎡R11R21R31R12R22R32R13R23R33⎦⎤
或者
R = [ c y c z − c y s z s y c z s x s y + c x s z c x c z − s x s y s z − c y s x − c x c z s y + s x s z c z s x + c x s y s z c x c y ] \mathrm{R}=\left[\begin{array}{ccc} c_y c_z & -c_y s_z & s_y \\ c_z s_x s_y+c_x s_z & c_x c_z-s_x s_y s_z & -c_y s_x \\ -c_x c_z s_y+s_x s_z & c_z s_x+c_x s_y s_z & c_x c_y \end{array}\right] R=⎣⎡cyczczsxsy+cxsz−cxczsy+sxsz−cyszcxcz−sxsyszczsx+cxsyszsy−cysxcxcy⎦⎤
旋转矩阵变换到欧拉角的公式:
{ ψ = tan − 1 R 12 R 22 θ = − sin − 1 R 13 φ = tan − 1 R 23 R 33 \left\{\begin{array}{l} \psi=\tan ^{-1} \frac{R_{12}}{R_{22}} \\ \theta=-\sin ^{-1} R_{13} \\ \varphi=\tan ^{-1} \frac{R_{23}}{R_{33}} \end{array}\right. ⎩⎨⎧ψ=tan−1R22R12θ=−sin−1R13φ=tan−1R33R23
4. 四元数
1843 年爱尔兰数学家哈密顿 (W.R.Hamilton) 发明了四元数, 即形如 q ˙ = q 0 + q 1 i + q 2 j + q 3 k \dot{q}=q_{0}+q_{1} i+q_{2} \boldsymbol{j}+q_{3} k q˙=q0+q1i+q2j+q3k 的超复数, 同时他也给出了四元数的加法、乘法规则以及四元数 的逆和模, 指出四元数能够通过旋转、伸长或缩短等变换将一个给定的矢量变成另一个矢量。四元数表达中, q 0 , q 1 , q 2 , q 3 q_{0}, q_{1}, q_{2}, q_{3} q0,q1,q2,q3 为任意实数, i , j , k i, j, k i,j,k 是虚数单位, 满足 i 2 = j 2 = k 2 = − 1 , j k = − k j = i , k i = − i k = j , i j = − j i = k ′ i^{2}=j^{2}=k^{2}=-1, j k=-k j=i, k i=-i k=j, i j=-j i=k^{\prime} i2=j2=k2=−1,jk=−kj=i,ki=−ik=j,ij=−ji=k′ 。 其中 q 0 + q 1 i + q 2 j + q 3 k q_{0}+q_{1} i+q_{2} j+q_{3} k q0+q1i+q2j+q3k 为四元数的代数形式, q 0 q_{0} q0 为四元数 q ˙ \dot{q} q˙ 的实部, q 1 i + q 2 j + q 3 k q_{1} \boldsymbol{i}+q_{2} \boldsymbol{j}+q_{3} \boldsymbol{k} q1i+q2j+q3k 为四元数 q ˙ \dot{q} q˙ 的虚部。
四元数是当前用于高分辨率光学遥感卫星在轨姿态测量与控制的常用姿态参数表达方式,不存在奇点情况,表达方式具有唯一性。
4.1 四元数与欧拉角和旋转矩阵之间等效变换
四元数与旋转矩阵变换为:
R = [ 2 q 0 2 + 2 q 1 2 − 1 2 q 1 q 2 − 2 q 0 q 3 2 q 1 q 3 + 2 q 0 q 2 2 q 1 q 2 + 2 q 0 q 3 2 q 0 2 + 2 q 2 2 − 1 2 q 2 q 3 − 2 q 0 q 1 2 q 1 q 3 − 2 q 0 q 2 2 q 2 q 3 + 2 q 0 q 1 2 q 0 2 + 2 q 3 2 − 1 ] \boldsymbol{R}=\left[\begin{array}{ccc} 2 q_{0}^{2}+2 q_{1}^{2}-1 & 2 q_{1} q_{2}-2 q_{0} q_{3} & 2 q_{1} q_{3}+2 q_{0} q_{2} \\ 2 q_{1} q_{2}+2 q_{0} q_{3} & 2 q_{0}^{2}+2 q_{2}^{2}-1 & 2 q_{2} q_{3}-2 q_{0} q_{1} \\ 2 q_{1} q_{3}-2 q_{0} q_{2} & 2 q_{2} q_{3}+2 q_{0} q_{1} & 2 q_{0}^{2}+2 q_{3}^{2}-1 \end{array}\right] R=⎣⎡2q02+2q12−12q1q2+2q0q32q1q3−2q0q22q1q2−2q0q32q02+2q22−12q2q3+2q0q12q1q3+2q0q22q2q3−2q0q12q02+2q32−1⎦⎤
欧拉角到四元数变换为:
{ q 0 = cos ψ 2 cos θ 2 cos φ 2 + sin ψ 2 sin θ 2 sin φ 2 q 1 = − cos ψ 2 cos θ 2 cos φ 2 + sin ψ 2 sin θ 2 sin φ 2 q 2 = − cos ψ 2 cos θ 2 cos φ 2 − sin ψ 2 sin θ 2 sin φ 2 q 3 = − cos ψ 2 cos θ 2 cos φ 2 + sin ψ 2 sin θ 2 sin φ 2 \left\{\begin{array}{l} q_{0}=\cos \frac{\psi}{2} \cos \frac{\theta}{2} \cos \frac{\varphi}{2}+\sin \frac{\psi}{2} \sin \frac{\theta}{2} \sin \frac{\varphi}{2} \\ q_{1}=-\cos \frac{\psi}{2} \cos \frac{\theta}{2} \cos \frac{\varphi}{2}+\sin \frac{\psi}{2} \sin \frac{\theta}{2} \sin \frac{\varphi}{2} \\ q_{2}=-\cos \frac{\psi}{2} \cos \frac{\theta}{2} \cos \frac{\varphi}{2}-\sin \frac{\psi}{2} \sin \frac{\theta}{2} \sin \frac{\varphi}{2} \\ q_{3}=-\cos \frac{\psi}{2} \cos \frac{\theta}{2} \cos \frac{\varphi}{2}+\sin \frac{\psi}{2} \sin \frac{\theta}{2} \sin \frac{\varphi}{2} \end{array}\right. ⎩⎪⎪⎨⎪⎪⎧q0=cos2ψcos2θcos2φ+sin2ψsin2θsin2φq1=−cos2ψcos2θcos2φ+sin2ψsin2θsin2φq2=−cos2ψcos2θcos2φ−sin2ψsin2θsin2φq3=−cos2ψcos2θcos2φ+sin2ψsin2θsin2φ
四元数变换为欧拉角:
{ ψ = tan − 1 2 q 1 q 2 − 2 q 0 q 3 2 q 0 2 + 2 q 1 2 − 1 θ = − sin − 1 ( 2 q 1 q 3 + 2 q 0 q 2 ) φ = tan − 1 2 q 2 q 3 − 2 q 0 q 1 2 q 0 2 + 2 q 3 2 − 1 \left\{\begin{array}{l} \psi=\tan ^{-1} \frac{2 q_{1} q_{2}-2 q_{0} q_{3}}{2 q_{0}^{2}+2 q_{1}^{2}-1} \\ \theta=-\sin ^{-1}\left(2 q_{1} q_{3}+2 q_{0} q_{2}\right) \\ \varphi=\tan ^{-1} \frac{2 q_{2} q_{3}-2 q_{0} q_{1}}{2 q_{0}^{2}+2 q_{3}^{2}-1} \end{array}\right. ⎩⎪⎨⎪⎧ψ=tan−12q02+2q12−12q1q2−2q0q3θ=−sin−1(2q1q3+2q0q2)φ=tan−12q02+2q32−12q2q3−2q0q1
四元数由四个数字组成,然而这些数字不表示角度或轴,并且通常不需要直接访问它们。除非你特别有兴趣深入了解四元数学,你只需要知道四元数表示三维空间中的旋转,你通常不需要知道或修改x,y和z属性。
优点:四元旋转不存在万向节锁问题。
优点:存储空间小,计算效率高。
弱点:单个四元数不能表示在任何方向上超过180度的旋转。
弱点:四元数的数字表示不直观。
参考:【Unity编程】四元数(Quaternion)与欧拉角
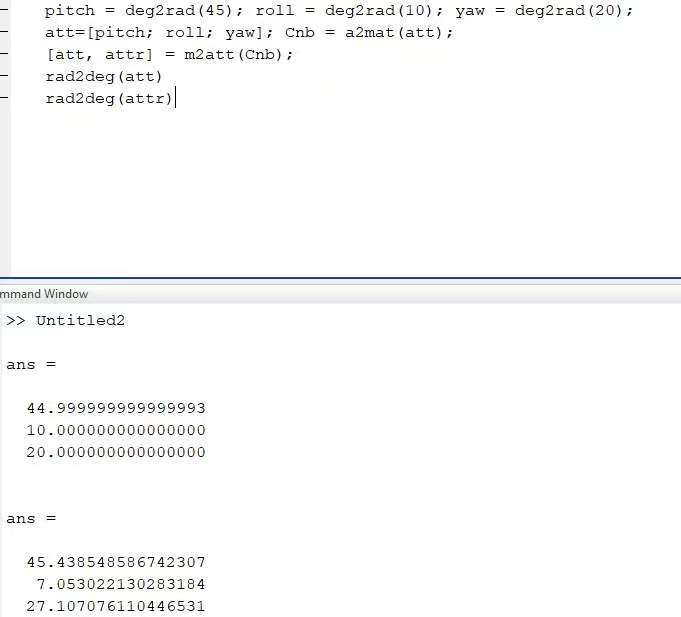
4.2 测试Matlab代码
验证测试:3D Rotation Converter
clc; clear; close all% Axis rotation sequence for the Euler angles, specified as one of these string scalars:
% "ZYX" (default) – The order of rotation angles is z-axis, y-axis, x-axis.
% "ZYZ" – The order of rotation angles is z-axis, y-axis, z-axis.
% "XYZ" – The order of rotation angles is x-axis, y-axis, z-axis.% 三个欧拉角
eul = deg2rad([30 60 90]);% 指定旋转顺序为XYZ
rotm = eul2rotm(eul,'XYZ') %欧拉角转旋转矩阵
quat = eul2quat(eul,'XYZ') %欧拉角转四元数eul = rad2deg(rotm2eul(rotm,'XYZ')) %旋转矩阵转欧拉角
quat = rotm2quat(rotm) %旋转矩阵转四元数eul = rad2deg(quat2eul(quat,'XYZ')) %四元数转欧拉角
rotm = quat2rotm(quat) %四元数转旋转矩阵
旋转矩阵
-2.22044604925031e-16 -0.500000000000000 0.866025403784439
0.866025403784439 -0.433012701892220 -0.250000000000000
0.500000000000000 0.750000000000000 0.433012701892219
四元数
0.500000000000000 0.500000000000000 0.183012701892219 0.683012701892219
5. 总结
本文分别描述了四元数与旋转矩阵、欧拉角与四元数、四元数与欧拉角之间的变化关系。欧拉角、旋转矩阵与四元数这三种表征姿态的方法各有其优劣。欧拉角在某种情况下会遇到万向锁问题,即会丢失一个自由度的信息;旋转矩阵里面有九个数值,而三维旋转一次只需要三个自由度,这会造成计算量有点大。而四元数没有欧拉角和旋转矩阵所特有的奇异性,可以很好地表征运动物体的姿态,故四元数表征姿态应用较多。