题目链接
反思
我们之前用 k m p kmp kmp都是用到前缀字串的最长匹配长度,本题则需要利用 p m t pmt pmt数组找到最短匹配长度
思路
题目中匹配前缀的意思是,在字符串 a a a的前缀中,某个前缀自身重复两遍后能把 a a a包括进来
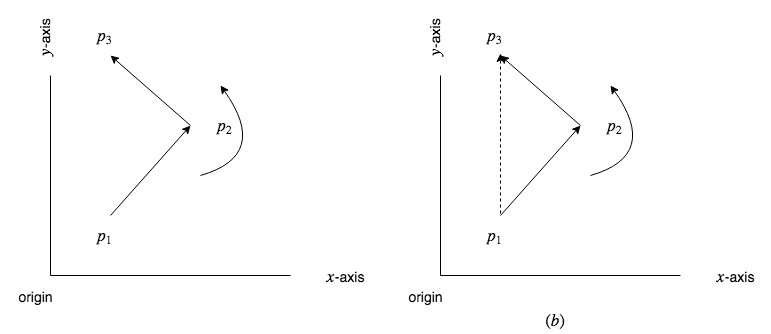
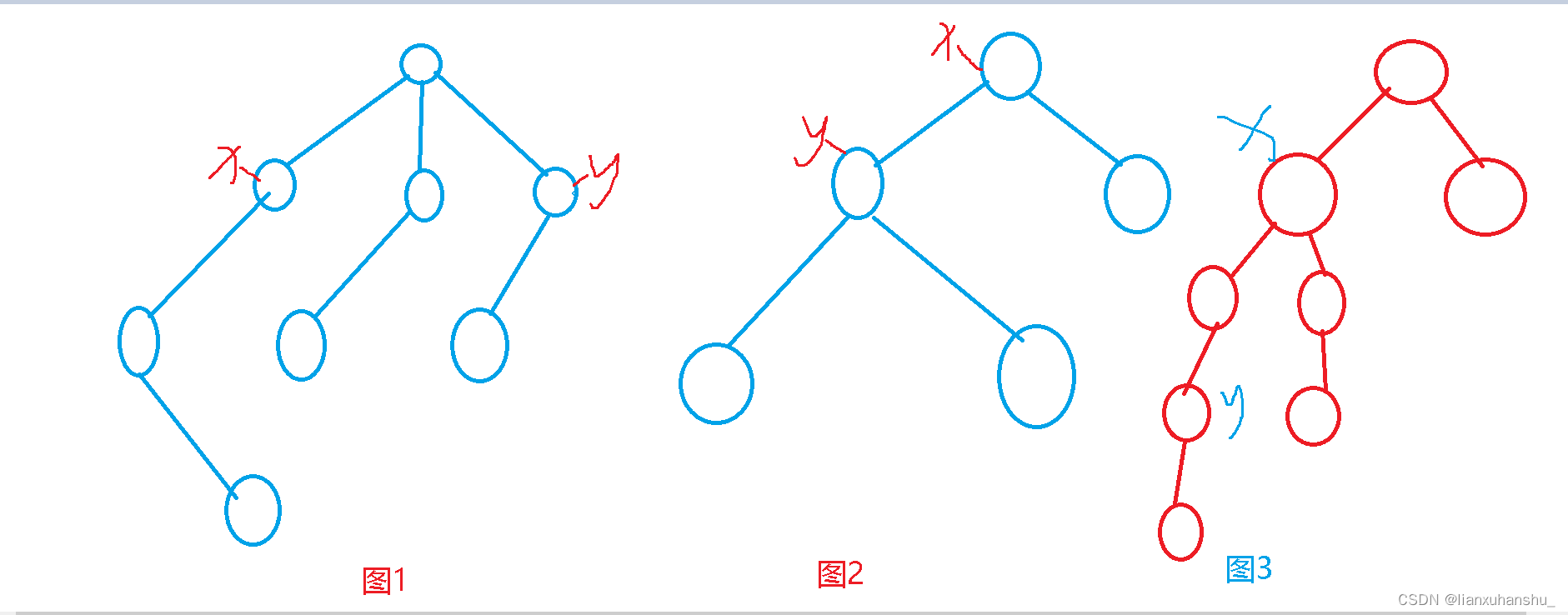
如图:
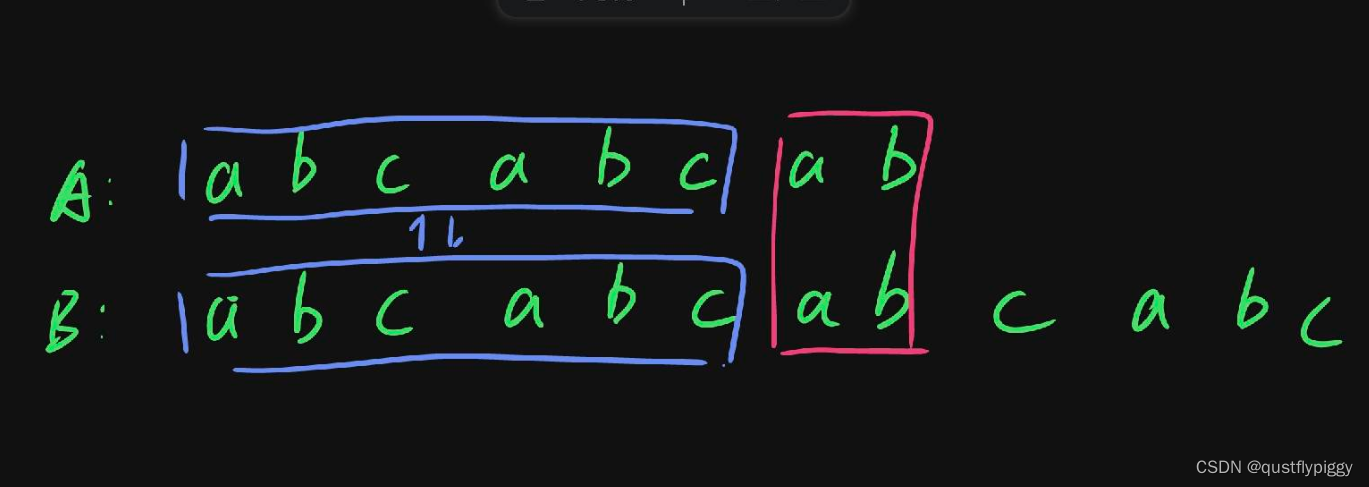
如图, A A A的最长匹配字段显然是 a b c a b c abcabc abcabc
同时容易发现, A [ 7 8 ] A[7~8] A[7 8]= A [ 1 2 ] A[1~2] A[1 2],满足 p m t pmt pmt数组的原则:前后缀相等。且我们要找最长匹配字段,所以要找到最短的匹配的前后缀长度,但 p m t pmt pmt只能找到最长匹配,要找到最短匹配,我们需要递推 p m t [ i ] , p m t [ p m t [ i ] ] . . . pmt[i],pmt[pmt[i]]... pmt[i],pmt[pmt[i]]...,直到等于 0 0 0,如上图, p m t [ 8 ] = 5 , p m t [ 5 ] = 2 , p m t [ 2 ] = 2 pmt[8]=5,pmt[5]=2,pmt[2]=2 pmt[8]=5,pmt[5]=2,pmt[2]=2,所以 p m t [ 5 ] = 2 pmt[5]=2 pmt[5]=2就是 8 8 8的最短匹配长度
ACcode
#include<bits/stdc++.h>using namespace std;using ll = long long;const int M = 1e6 + 9;
ll pmt[M];void get_pmt(const string& p) {for (int i = 1, j = 0;i < p.size();i++) {while (j && p[i] != p[j])j = pmt[j - 1];if (p[i] == p[j])j++;pmt[i] = j;}
}int main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);ll n;cin >> n;string str;cin >> str;get_pmt(str);ll ans = 0;for (int i = 2, j = 2;i <= str.size();i++, j = i) {while (pmt[j - 1])j = pmt[j - 1];if (pmt[i - 1])pmt[i - 1] = j;ans += i - j;}cout << ans;return 0;
}