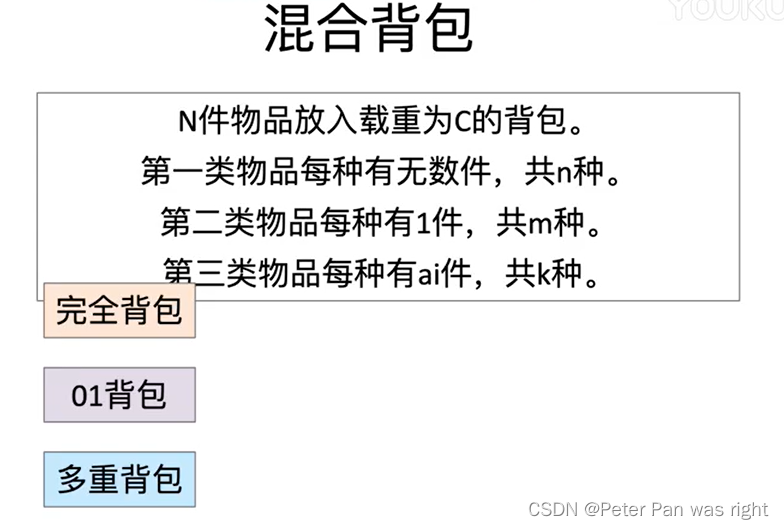
确定两条连续线段向左转还是向右转

一、说明

   如果是作图，或者是判别小车轨迹。为了直观地了解，从当前点到下一个点过程中，什么是左转、什么是右转，或者方向不变，这在现场实时运算中是很重要的。本篇描述其快速算法。

   请考虑下面所示的示例。

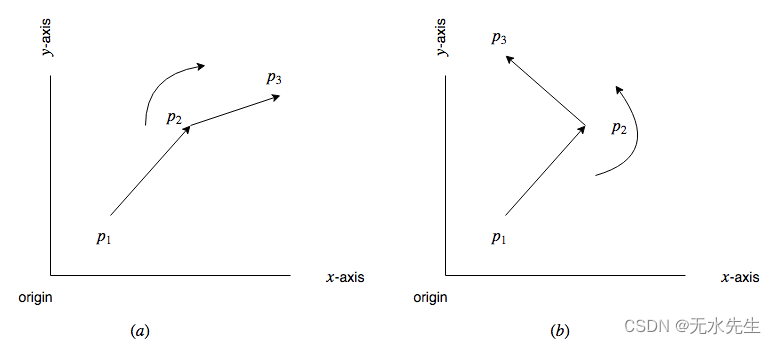
   两图中，共有三点p1,p2和p3和两条线段$\overline{p_1{p}_2}$和$\overline{p_2{p}_3}$。中途点$p_2$是两条线段共有的。在图（a）中，线段$\overline{p_2{p}_3}$在$p_2$该点右转而在图（b）中，段$\overline{p_2{p}_3}$在公共点$p_2$左转。我们的眼睛更容易通过观察图形来快速识别路段是左转还是右转，因为您的眼睛天生具有快速识别事物的能力。在这篇文章中，我将讨论计算机如何使用几何算法来识别这一点。

二、算法

2.1 两点的叉积

   给定两点$p_1(x_1,y_1）$和$p_2(x_2,y_2)$，我们首先需要判断点是否$p_1$从点开始是顺时针还是逆时针$p_2$就起源而言。解决这个问题的一种方法是计算两者所成的角度$\overline{p_1}$和$\overline{p_2}$
和X轴和角度的差异可以判断一个点是顺时针还是逆时针。有一个比查找计算向量叉积的角度更简单有效的解决方案$\overline{p_1}$和$\overline{p_2}$。数学上两个向量的叉积$\overline{p_1}$和$\overline{p_2}$定义成：
$$p_1\times p_2=x_1{y}_2-x_2{y}_1$$

   如果值p1×p2则为正,p1是沿逆时针到达p2，关于原点如下图所示。

   同样，如果p1×p2是负数，从p1到p2是顺时针过度。相对于原点，如果值为 0，则点p1,p2和原点共线。以下 python 代码实现了叉积。

class Point:def __init__(self, x, y):self.x = xself.y = ydef subtract(self, p):return Point(self.x - p.x, self.y - p.y)def __str__(self):return '(' + str(self.x) + ', ' + str(self.y) + ')'# calculates the cross product of vector p1 and p2
# if p1 is clockwise from p2 wrt origin then it returns +ve value
# if p2 is anti-clockwise from p2 wrt origin then it returns -ve value
# if p1 p2 and origin are collinear then it returs 0
def cross_product(p1, p2):return p1.x * p2.y - p2.x * p1.y

2.2 两个段的叉积

   考虑两个线段，其端点是p1（X1,y1）,p2（X2,y2）和p1（X1,y1）,p3（X3,y3）分别。为了计算两个线段的叉积，我们需要将它们转换为向量。这可以通过以下方式完成。

$$\overline{p_1{p}_2}=(x_2-x_1,y_2-y_1),\overline{p_1{p}_3}=(x_3-x_1,y_3-y_1)$$

   一旦我们有了两个两个向量，我们就可以调用cross_product来计算叉积，如下面的代码所示。

# returns the cross product of vector p1p3 and p1p2
# if p1p3 is clockwise from p1p2 it returns +ve value
# if p1p3 is anti-clockwise from p1p2 it returns -ve value
# if p1 p2 and p3 are collinear it returns 0
def direction(p1, p2, p3):return  cross_product(p3.subtract(p1), p2.subtract(p1))

三、旋转方向判别

3.1 左转

   判断一个段是否$p_2{p}_3$从路段左转$p_1{p}_2$在点$p_2$，我们画下一个向量$\overline{p_1{p}_3}$并检查新向量是否与向量逆时针方向$\overline{p_2{p}_3}$。如下图所示。右图显示向量
在这里插入代码片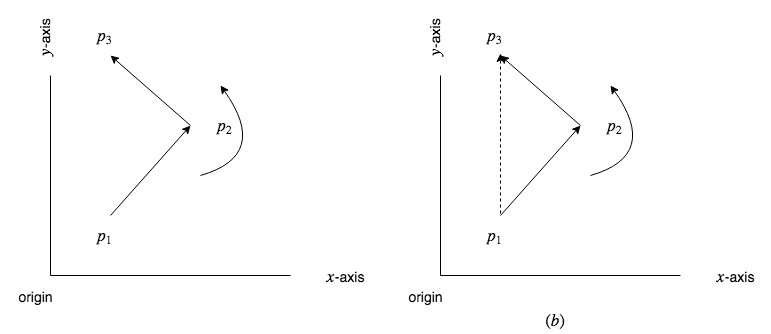

   $\overline{p_1{p}_3}$从向量逆时针方向$\overline{p_1{p}_2}$因此我们可以说该段p2p3
从路段左转p1p2在点p2。下面给出了 python 实现。

# checks if p3 makes left turn at p2
def left(p1, p2, p3):return direction(p1, p2, p3) < 0

3.2 右转

   这与左转相同，唯一的区别是向量$\overline{p_1{p}_3}$从向量顺时针方向$\overline{p_2{p}_3}$。下面给出了 python 实现。

# checks if p3 makes right turn at p2
def right(p1, p2, p3):return direction(p1, p2, p3) > 0

3.3 共线判别

   当该方法direction既不返回正值也不返回负值而是返回零时，就会出现一种特殊情况。在这种情况下，所有的点$p_1$,$p_2$和$p_3$位于同一条线上。在本例中段$p_2{p}_3$不转向任何方向。

# checks if p1, p2 and p3 are collinear
def collinear(p1, p2, p3):return direction(p1, p2, p3) == 0

参考
Cormen, TH、Leiserson, CE、Rivest, RL 和 Stein, C.（nd）。算法简介（第三版）。麻省理工学院出版社。