标题略有夸张的表达了接下来这一套确实很简单,相较于直接下载或者通过秋叶包更新而言。大大节省磁盘空间,和下载时间。
这篇教程不需要你有:
- 代码基础。都是复制粘贴就完事。
- 魔法。
这篇教程默认你已经有:
- 1. 本地能够正常使用的sd webui。无论是自己源码安装的,还是使用的秋叶包。如果没有的话就不适合哈。
- 2. git环境。能从github上拉源码下来。这个教程很多就不多赘述了。第一次接触的话,学到能拉取代码到本地就可以,其他复杂的代码内容不用看,因为用不到。
- 3. windows环境。
以下是正文:
====
1. 首先你需要把ComfyUI的源码克隆到本地来。
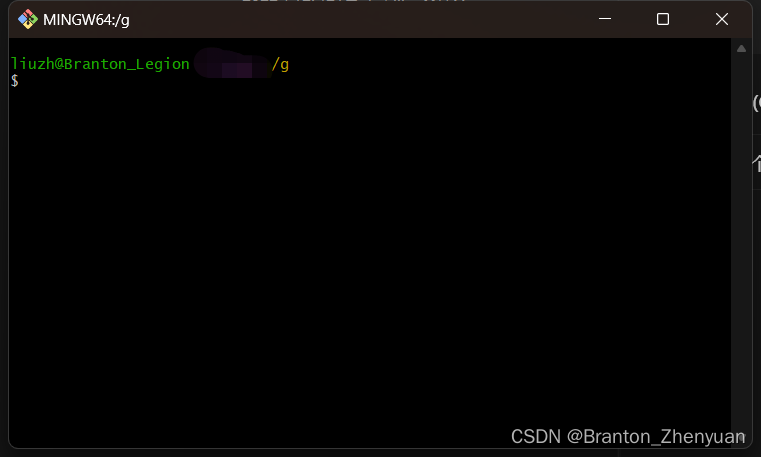
step1:找到你要把ComfyUI放到哪里的位置
操作:右键--显示更多选项--Git bash here
step2:通过代理网站ghproxy.com把github上对应的comfyui的代码拉下来。不需要新建文件夹,重命名哈,git clone的时候会自动创建一个。
操作:在打开的git面板中复制粘贴(用shift+insert粘贴,不是ctrl+v)这段代码,回车。
git clone https://ghproxy.com/https://github.com/comfyanonymous/ComfyUI.git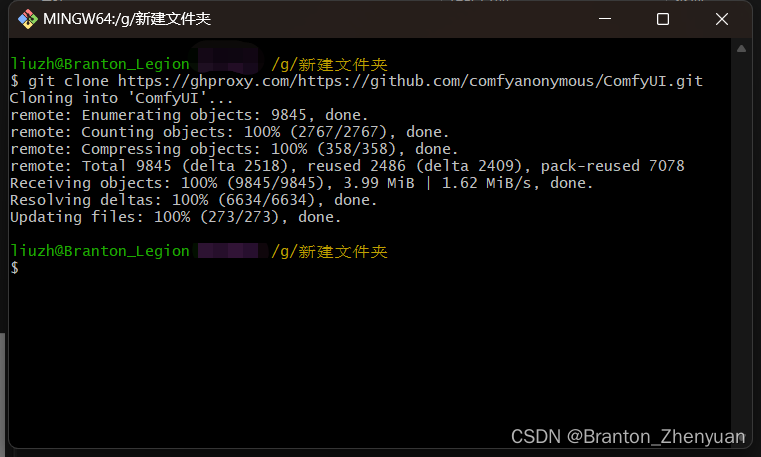 这里应该正常网速也应该10s就能好。远比从官方代码库下一个1个多G的安装包要快很多。
这里应该正常网速也应该10s就能好。远比从官方代码库下一个1个多G的安装包要快很多。
2. 把ComfyUI中的模型文件夹指向sd webui的。
step1:进入 ComfyUI_windows_portable\ComfyUI文件夹,找到 extra_model_paths.yaml.example文件,进行修改,以便ComfyUI可以直接用WebUI下已经下好的模型。
操作:修改第七行 改为 sd webui所在的总路径。保存后关闭。
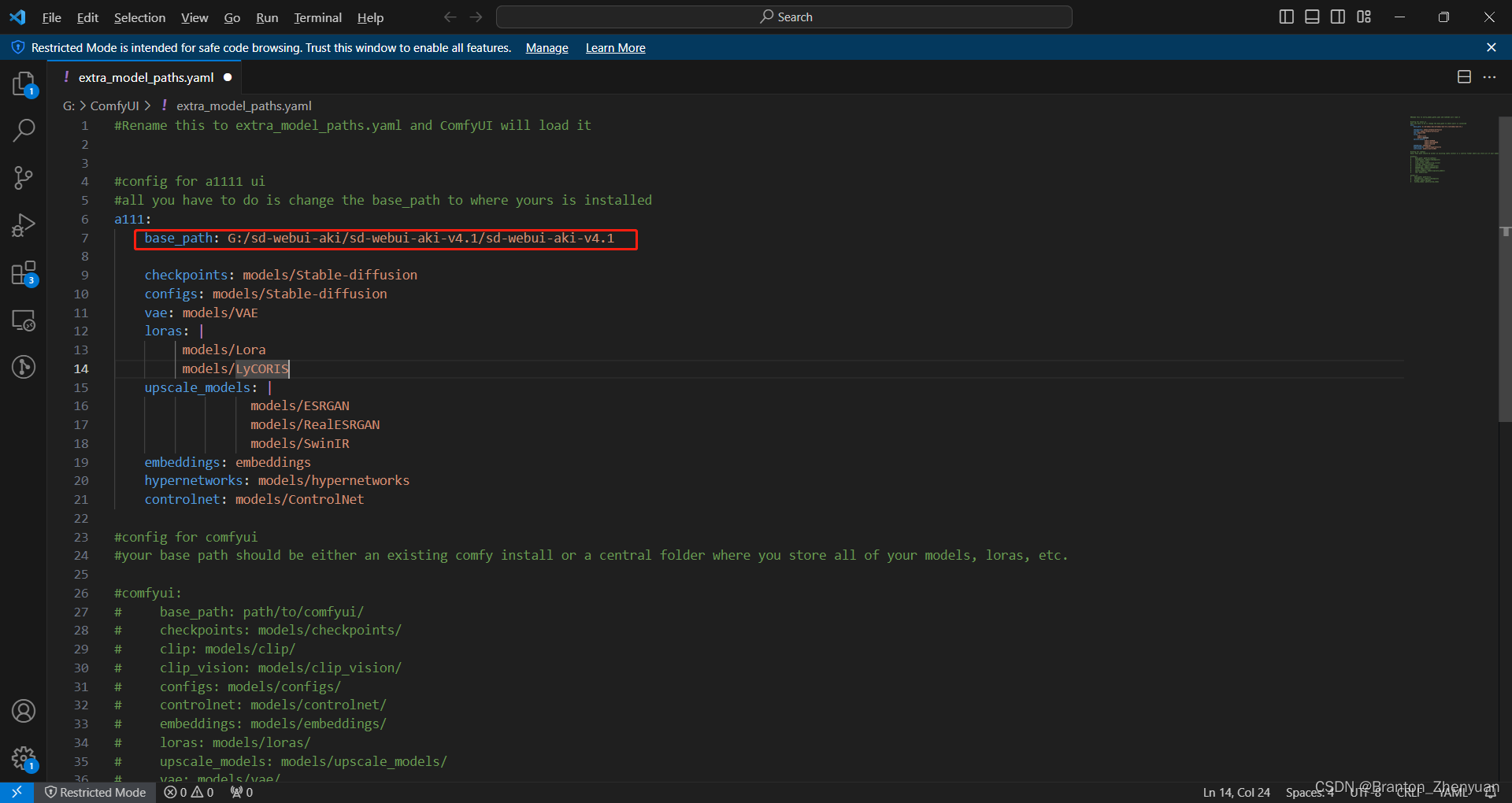
也就是这个路径
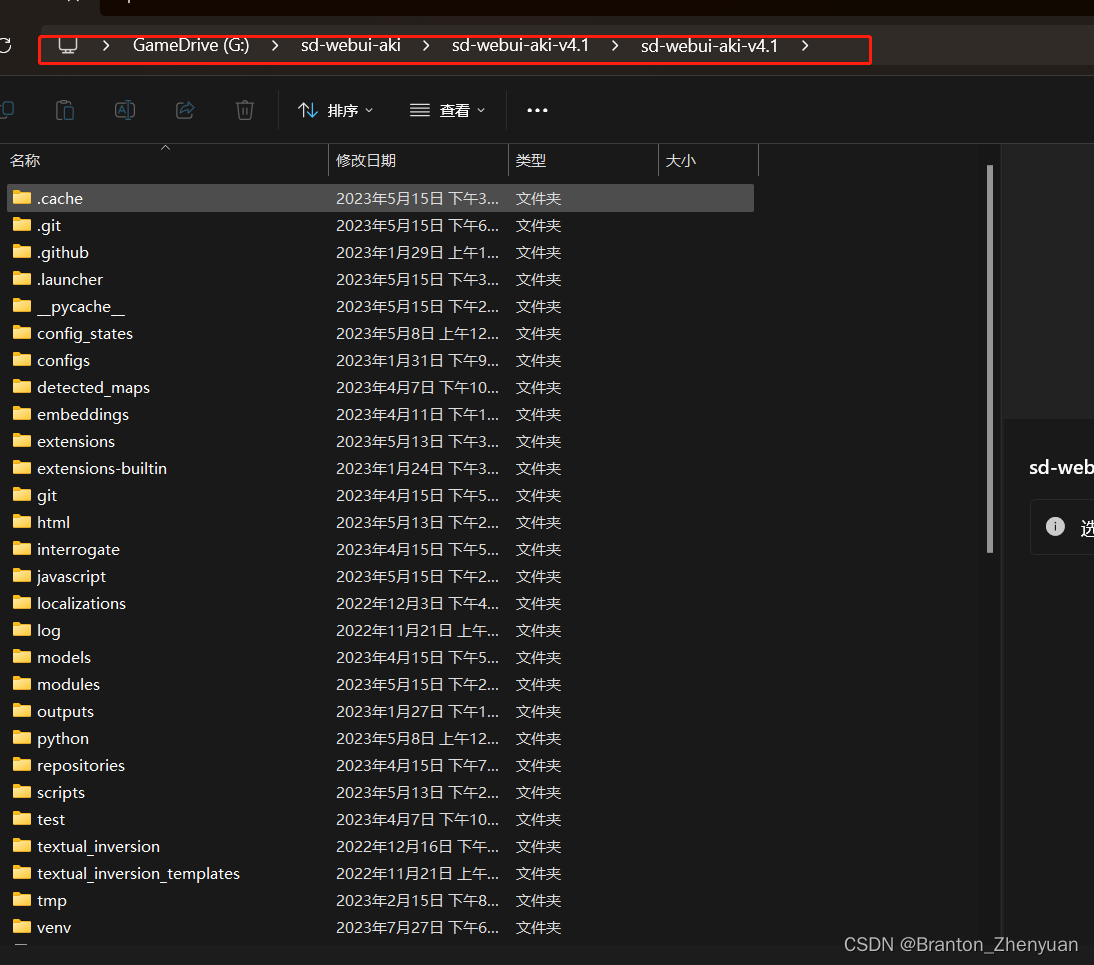
3. 最后一步,用sd webui的环境把ComfyUI跑起来。
这里有两种情况:
如果你是自己安装的那么你的sd webui的环境大概率是在这个路径下:
"G:\xxx\stable-diffusion-webui\venv\Scripts\activate.bat"
如果你是秋叶包的那么你的sd webui的环境大概率是在这个路径下:
"G:\xxx\sd-webui-aki\sd-webui-aki-v4.1\sd-webui-aki-v4.1\python\Scripts\activate.bat"
G:\xxx 这里换成你自己的上层目录即可。
step1:把这个环境启动起来,通过cmd(命令提示符)。
操作:按win键输入cmd回车。然后输入刚才找到的路径,包括引号回车。快捷操作可以通过选中那个.bat文件,按ctrl+shift+c复制到这个文件的路径,然后在cmd中用shift+insert粘贴。
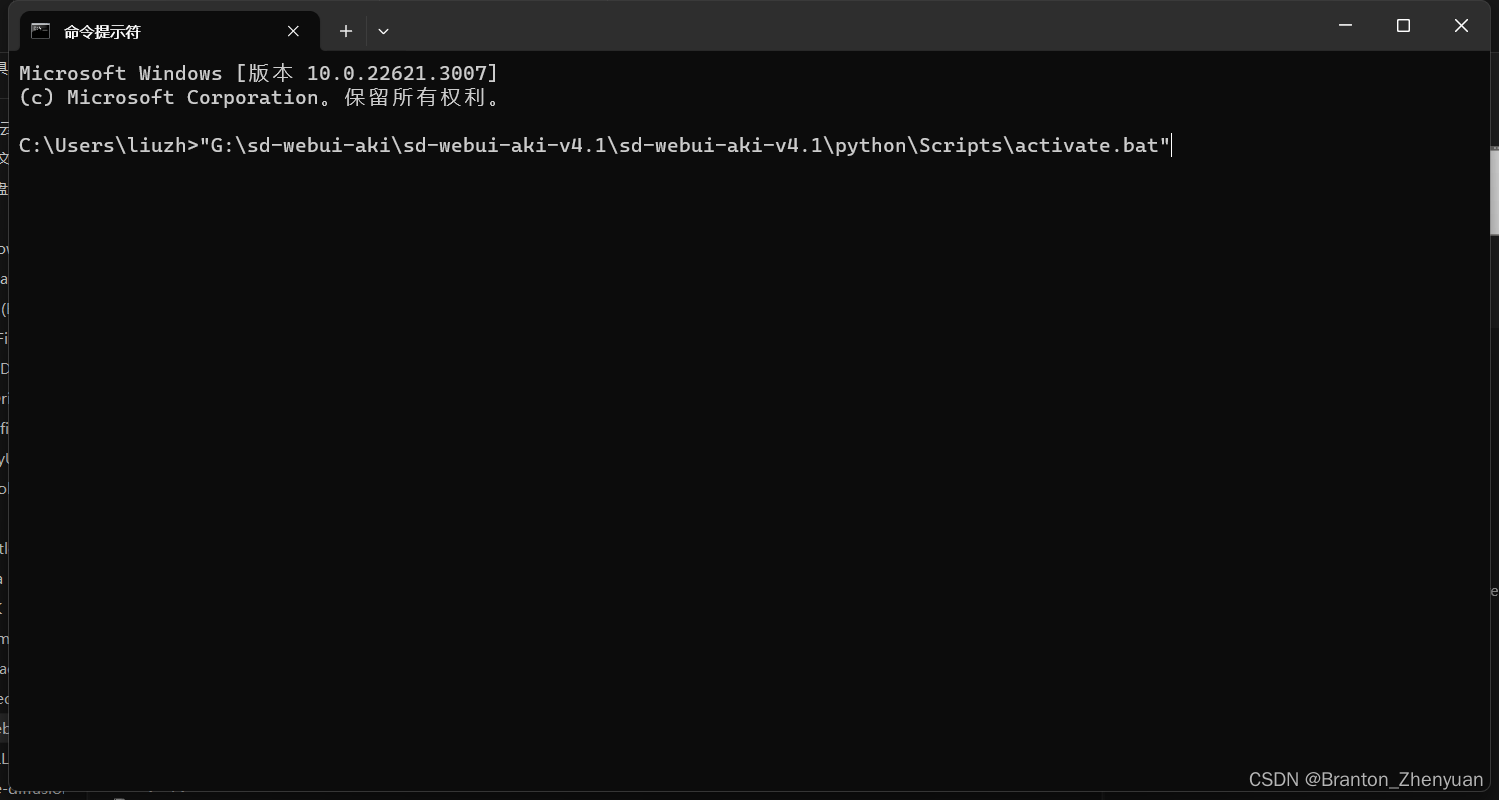
回车之后应该就进入这个python环境中了。前面括号里是当时创建的环境名称, 秋叶版的就会显示为python。
step2:启动comfyui的脚本。
操作:找到comfyui中的main.py文件,也就是以后用来启动comfyui的文件。在刚才打开的环境中输入后回车:
python G:\ComfyUI\main.pyPS: G:/替换为自己的路径。注意:区分/ \。
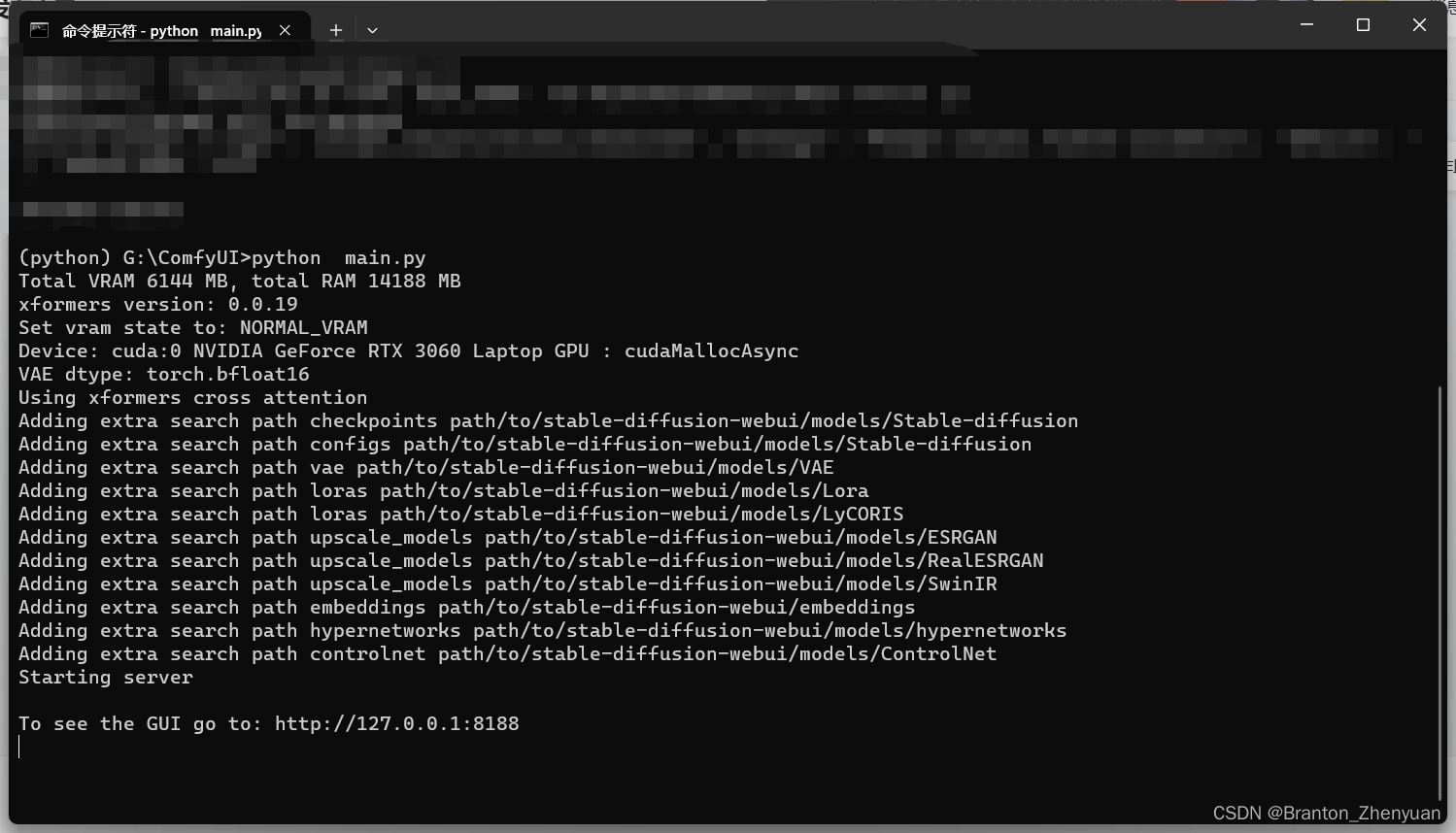
看到最后一行 http://127.0.0.2:8188 就说明启动成功了。按住ctrl鼠标点击这个地址就会打开comfyUI的界面。初次尝试记得替换这个位置的模型,不然会报错找不到默认的模型文件。
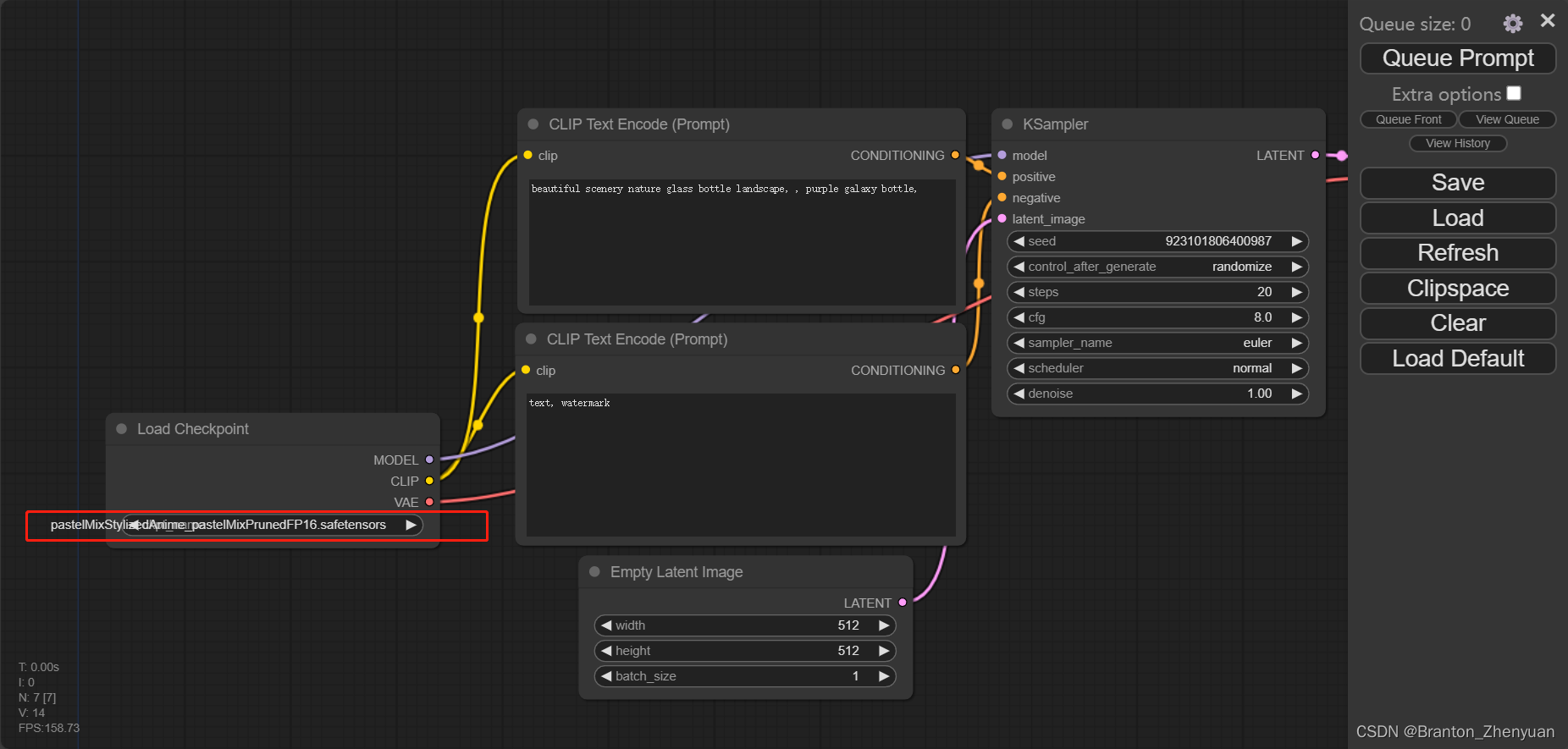
下次启动执行,重复第三步就可以。有人看,我再写一些怎么优化启动这里 。
就这样 Good Luck!