哈喽~各位过年好哇!
相信大家应该都看了春晚刘谦表演的魔术吧,大家当时有没有跟着做成功呢,其实背后的原理很简单,现在我们来逐句分析,一起探索其中的原理吧!
首先,有四张牌假设为1,2,3,4。然后撕一半,假设撕完之后的牌后为:1,2,3,4,1`,2`,3`,4`。然后有数字的牌面向下,放在一起之后,编号依次令为:4`,3`,2`,1`,4,3,2,1。
这样准备工作就做好了。接着就进入正题。
Step①:根据名字的字数依次从最上面的牌放到最下方
其实,这一步与几个字完全没任何关系,假如你是两个字,在完成这一步之后,牌序列变为:2`,1`,4,3,2,1,4`,3`;假如你是三个字,在完成这一步之后,牌序列变为:1`,4,3,2,1,4`,3`,2`。如果你的名字是七个字,在完成这一步之后,牌序列变为:1,4`,3`,2`,1`,4,3,2。
好了,接下来关键的一步,拿起最上面的3张牌,放进剩余牌的中间任意位置。
我先解释一下,首先3张牌的目的是为了保证拿起这3张牌之后的最上面一张牌的编号与最底下的一张牌的编号一定是对应的。假如你的名字是2个字:2`,1`,4,3,2,1,4`,3`,拿起3张牌之后剩下的牌变为3,2,1,4`,3`,可以发现3与3`是对应的。假如你的名字是3个字:1`,4,3,2,1,4`,3`,2`,2与2`也是对应的关系。同理其他序列也是满足的。
其次,这3张牌插进剩下牌的中间任意位置是为了保证不影响首尾这两张牌的对应关系,因此这里只需要将这3张牌插进中间的任意位置即可,并不会影响首尾的两张牌。
好了,在按照上述要求完成第一步之后,假设牌序列为:2,1,1`,4,3,4`,3`,2`。这样第一步就完成了。
Step②:将最上面的一张牌藏起来
此时最上面的一张牌为2,暂时藏起来。
此时牌序列变为:1,1`,4,3,4`,3`,2`。
Step③:南方人拿起1张牌,北方人拿起2张牌,不确定拿起3张牌,并将拿起来的牌插进剩下牌的中间任意位置
其实这里你不管拿起1张,2张还是3张无关竟要,然后将拿起的牌插进剩下牌的中间任意位置(小尼就是这里出现了失误,不小心把一张牌放到了最后一张牌的后面哈哈),这里插进中间任意位置的原因与Step1类似,并不会影响最后一张牌的位置。
假设我拿起3张牌,这一步之后牌的序列为:3,4`,1,1`,4,3`,2`。
Step④:男生拿起1张牌,女生拿起2张牌,并将拿起的牌扔掉
如果我拿起1张牌,并将这张牌扔掉之后,牌的序列变为:4`,1,1`,4,3`,2`;
如果我拿起2张牌,并将这2张牌扔掉之后,牌的序列变为:1,1`,4,3`,2`。
Step⑤:“见证奇迹的时刻”
完成这个操作之后,
如果你是男生,手里的牌序列应该为:1,1`,4,3`,2`,4`。
如果你是女生,手里的牌序列应该为:4,3`,2`,1,1`。
Step⑥:“好运留下来,烦恼丢出去”
好了,进入正题。这里本质就是约瑟夫环问题(Josephus)。(如果有不太了解约瑟夫环的朋友,可以看我之前写的这篇文章比较详细:约瑟夫环问题(Josephus)-CSDN博客)
为了简单起见,本篇文章用最简单的数组来模拟实现约瑟夫环问题。
如果你是男生,此时手里还剩下6张牌,序列依次为:1,1`,4,3`,2`,4`;(2`编号为5)
如果你是女生,此时手里还剩下5张牌,手里的牌序列应该为:4,3`,2`,1,1`。(2`编号为3)
现在我们先一步一步操作,来观察一下每一步剩余牌的序列:
·假设还剩6张牌(1,1`,4,3`,2`,4`)
1)1放到最后面,1`扔掉。
序列变为:4,3`,2`,4`,1。
2)4放到最后面,3`扔掉。
序列变为:2`,4`,1,4。
3)2`放到最后面,4`扔掉。
序列变为:1,4,2`。
4)1放到最后面,4扔掉。
序列变为:2`,1。
5)2`放到最后面,1扔掉。
序列变为:2`。
扔掉牌的序列依次为:1`,3`,4`,4,1。
·假设还剩5张牌(4,3`,2`,1,1`)
1)4放到最后面,3`扔掉。
序列变为:2`,1,1`,4。
2)2`放到最后面,1扔掉。
序列变为:1`,4,2`。
3)1`放到最后面,4扔掉。
序列变为:2`,1`。
4)2`放到最后面,1`扔掉。
序列变为:2`。
扔掉牌的序列依次为:3`,1,4,1`。
通过上面逐步分析,可以发现无论你最后还剩6张牌还是5张牌,出局序列都是约瑟夫环的淘汰序列。
注意看我紫色标记的数字以及对应的下标位置(假设编号从1开始),此时其他位置的牌是什么数字已经无所谓了,可以理解为只是一个名字代号而已。现在只需要关心接下来约瑟夫环的淘汰顺序即可。
如果此时手里还剩下6张牌,转化为约瑟夫环问题,这里就相当于总人数为6,从编号为1的人开始从“1”报数,报数为“2”的人出局。
代码如下:
Code1:
#include<iostream>
#define n 6 // 总人数
#define m 2 // 出局数字
#define k 1 // 第k个人开始报数
using namespace std;int main()
{int a[n+1];int i;int count=0; // 报数int out_count=0; // 出圈人数数量for(i=1;i<=n;i++)a[i]=i; // 给每个人编号 1~N (即将数组 a[1]~a[N] 分别赋值为 1~N) i=k; // 第i个开始报数cout<<"最后出队序列编号为:";while(out_count!=n){if(a[i]!=0) // 编号为 0 直接跳过 {count++;if(count==m){cout<<a[i]<<' '; a[i]=0; // 出圈记为 0 out_count++; // 出圈人数数量 +1 count=0; // 每出圈一个人重新计数 }}i++;if(i==n+1) // 若 i 超过数组最大下标,则 i 从第一个下标重新开始 i=1; }cout<<endl;
} 代码运行结果为:
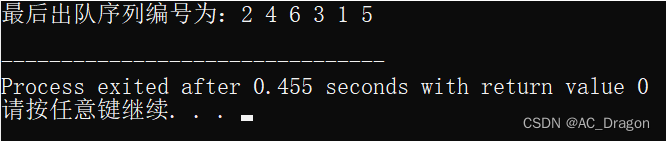
通过运行结果可以发现:
出局的编号依次为2,4,6,3,1,5,所对应的牌依次为:1`,3`,4`,4,1,2`,可以发现最后剩下的1张牌2`与Step②藏的2正好对应了起来。
如果此时手里还剩下5张牌,转化为约瑟夫环问题,这里就相当于总人数为5,从编号为1的人开始从“1”报数,报数为“2”的人出局。
代码如下:(只需将宏定义的n改为5即可)
Code2:
#include<iostream>
#define n 5 // 总人数
#define m 2 // 出局数字
#define k 1 // 第k个人开始报数
using namespace std;int main()
{int a[n+1];int i;int count=0; // 报数int out_count=0; // 出圈人数数量for(i=1;i<=n;i++)a[i]=i; // 给每个人编号 1~N (即将数组 a[1]~a[N] 分别赋值为 1~N) i=k; // 第i个开始报数cout<<"最后出队序列编号为:";while(out_count!=n){if(a[i]!=0) // 编号为 0 直接跳过 {count++;if(count==m){cout<<a[i]<<' '; a[i]=0; // 出圈记为 0 out_count++; // 出圈人数数量 +1 count=0; // 每出圈一个人重新计数 }}i++;if(i==n+1) // 若 i 超过数组最大下标,则 i 从第一个下标重新开始 i=1; }cout<<endl;
} 运行结果如下:
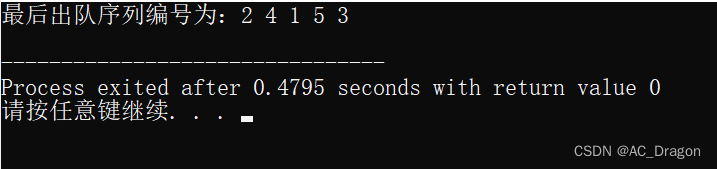
通过运行结果可以发现:
出局的编号依次为2,4,1,5,3,所对应的牌依次为:3`,1,4,1`,2`,可以发现最后剩下的1张牌2`与Step②藏的2正好对应了起来。
这样我们就成功地梳理了一遍魔术的流程,并且用C语言验证了结果。
你们理解其中的原理了吗?