目录
手写数字识别之网络结构
数据处理
经典的全连接神经网络
卷积神经网络
手写数字识别之网络结构
无论是牛顿第二定律任务,还是房价预测任务,输入特征和输出预测值之间的关系均可以使用“直线”刻画(使用线性方程来表达)。但手写数字识别任务的输入像素和输出数字标签之间的关系显然不是线性的,甚至这个关系复杂到我们靠人脑难以直观理解的程度。

图1:数字识别任务的输入和输出不是线性关系
因此,我们需要尝试使用其他更复杂、更强大的网络来构建手写数字识别任务,观察一下训练效果,即将“横纵式”教学法从横向展开,如 图2 所示。本节主要介绍两种常见的网络结构:经典的多层全连接神经网络和卷积神经网络。

图2:“横纵式”教学法 — 网络结构优化
数据处理
#数据处理部分之前的代码,保持不变
import os
import random
import paddle
import numpy as np
import matplotlib.pyplot as plt
from PIL import Imageimport gzip
import json# 定义数据集读取器
def load_data(mode='train'):# 加载数据datafile = './work/mnist.json.gz'print('loading mnist dataset from {} ......'.format(datafile))data = json.load(gzip.open(datafile))print('mnist dataset load done')# 读取到的数据区分训练集,验证集,测试集train_set, val_set, eval_set = data# 数据集相关参数,图片高度IMG_ROWS, 图片宽度IMG_COLSIMG_ROWS = 28IMG_COLS = 28if mode == 'train':# 获得训练数据集imgs, labels = train_set[0], train_set[1]elif mode == 'valid':# 获得验证数据集imgs, labels = val_set[0], val_set[1]elif mode == 'eval':# 获得测试数据集imgs, labels = eval_set[0], eval_set[1]else:raise Exception("mode can only be one of ['train', 'valid', 'eval']")#校验数据imgs_length = len(imgs)assert len(imgs) == len(labels), \"length of train_imgs({}) should be the same as train_labels({})".format(len(imgs), len(labels))# 定义数据集每个数据的序号, 根据序号读取数据index_list = list(range(imgs_length))# 读入数据时用到的batchsizeBATCHSIZE = 100# 定义数据生成器def data_generator():if mode == 'train':random.shuffle(index_list)imgs_list = []labels_list = []for i in index_list:img = np.array(imgs[i]).astype('float32')label = np.array(labels[i]).astype('float32')# 在使用卷积神经网络结构时,uncomment 下面两行代码img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')label = np.reshape(labels[i], [1]).astype('float32')imgs_list.append(img) labels_list.append(label)if len(imgs_list) == BATCHSIZE:yield np.array(imgs_list), np.array(labels_list)imgs_list = []labels_list = []# 如果剩余数据的数目小于BATCHSIZE,# 则剩余数据一起构成一个大小为len(imgs_list)的mini-batchif len(imgs_list) > 0:yield np.array(imgs_list), np.array(labels_list)return data_generator经典的全连接神经网络
经典的全连接神经网络来包含四层网络:输入层、两个隐含层和输出层,将手写数字识别任务通过全连接神经网络表示,如 图3 所示。

图3:手写数字识别任务的全连接神经网络结构
- 输入层:将数据输入给神经网络。在该任务中,输入层的尺度为28×28的像素值。
- 隐含层:增加网络深度和复杂度,隐含层的节点数是可以调整的,节点数越多,神经网络表示能力越强,参数量也会增加。在该任务中,中间的两个隐含层为10×10的结构,通常隐含层会比输入层的尺寸小,以便对关键信息做抽象,激活函数使用常见的Sigmoid函数。
- 输出层:输出网络计算结果,输出层的节点数是固定的。如果是回归问题,节点数量为需要回归的数字数量。如果是分类问题,则是分类标签的数量。在该任务中,模型的输出是回归一个数字,输出层的尺寸为1。
说明:
隐含层引入非线性激活函数Sigmoid是为了增加神经网络的非线性能力。
举例来说,如果一个神经网络采用线性变换,有四个输入x1x_1x1~x4x_4x4,一个输出yyy。假设第一层的变换是z1=x1−x2z_1=x_1-x_2z1=x1−x2和z2=x3+x4z_2=x_3+x_4z2=x3+x4,第二层的变换是y=z1+z2y=z_1+z_2y=z1+z2,则将两层的变换展开后得到y=x1−x2+x3+x4y=x_1-x_2+x_3+x_4y=x1−x2+x3+x4。也就是说,无论中间累积了多少层线性变换,原始输入和最终输出之间依然是线性关系。
Sigmoid是早期神经网络模型中常见的非线性变换函数,通过如下代码,绘制出Sigmoid的函数曲线。
def sigmoid(x):# 直接返回sigmoid函数return 1. / (1. + np.exp(-x))# param:起点,终点,间距
x = np.arange(-8, 8, 0.2)
y = sigmoid(x)
plt.plot(x, y)
plt.show()
<Figure size 432x288 with 1 Axes>
针对手写数字识别的任务,网络层的设计如下:
- 输入层的尺度为28×28,但批次计算的时候会统一加1个维度(大小为batch size)。
- 中间的两个隐含层为10×10的结构,激活函数使用常见的Sigmoid函数。
- 与房价预测模型一样,模型的输出是回归一个数字,输出层的尺寸设置成1。
下述代码为经典全连接神经网络的实现。完成网络结构定义后,即可训练神经网络。
import paddle.nn.functional as F
from paddle.nn import Linear# 定义多层全连接神经网络
class MNIST(paddle.nn.Layer):def __init__(self):super(MNIST, self).__init__()# 定义两层全连接隐含层,输出维度是10,当前设定隐含节点数为10,可根据任务调整self.fc1 = Linear(in_features=784, out_features=10)self.fc2 = Linear(in_features=10, out_features=10)# 定义一层全连接输出层,输出维度是1self.fc3 = Linear(in_features=10, out_features=1)# 定义网络的前向计算,隐含层激活函数为sigmoid,输出层不使用激活函数def forward(self, inputs):# inputs = paddle.reshape(inputs, [inputs.shape[0], 784])outputs1 = self.fc1(inputs)outputs1 = F.sigmoid(outputs1)outputs2 = self.fc2(outputs1)outputs2 = F.sigmoid(outputs2)outputs_final = self.fc3(outputs2)return outputs_final卷积神经网络
虽然使用经典的全连接神经网络可以提升一定的准确率,但其输入数据的形式导致丢失了图像像素间的空间信息,这影响了网络对图像内容的理解。对于计算机视觉问题,效果最好的模型仍然是卷积神经网络。卷积神经网络针对视觉问题的特点进行了网络结构优化,可以直接处理原始形式的图像数据,保留像素间的空间信息,因此更适合处理视觉问题。
卷积神经网络由多个卷积层和池化层组成,如 图4 所示。卷积层负责对输入进行扫描以生成更抽象的特征表示,池化层对这些特征表示进行过滤,保留最关键的特征信息。

图4:在处理计算机视觉任务中大放异彩的卷积神经网络
两层卷积和池化的神经网络实现如下所示。
# 定义 SimpleNet 网络结构
import paddle
from paddle.nn import Conv2D, MaxPool2D, Linear
import paddle.nn.functional as F
# 多层卷积神经网络实现
class MNIST(paddle.nn.Layer):def __init__(self):super(MNIST, self).__init__()# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)# 定义池化层,池化核的大小kernel_size为2,池化步长为2self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)# 定义池化层,池化核的大小kernel_size为2,池化步长为2self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)# 定义一层全连接层,输出维度是1self.fc = Linear(in_features=980, out_features=1)# 定义网络前向计算过程,卷积后紧接着使用池化层,最后使用全连接层计算最终输出# 卷积层激活函数使用Relu,全连接层不使用激活函数def forward(self, inputs):x = self.conv1(inputs)x = F.relu(x)x = self.max_pool1(x)x = self.conv2(x)x = F.relu(x)x = self.max_pool2(x)x = paddle.reshape(x, [x.shape[0], -1])x = self.fc(x)return x使用MNIST数据集训练定义好的卷积神经网络,如下所示。
说明:
以上数据加载函数load_data返回一个数据迭代器train_loader,该train_loader在每次迭代时的数据shape为[batch_size, 784],因此需要将该数据形式reshape为图像数据形式[batch_size, 1, 28, 28],其中第二维代表图像的通道数(在MNIST数据集中每张图片的通道数为1,传统RGB图片通道数为3)。
#网络结构部分之后的代码,保持不变
def train(model):model.train()#调用加载数据的函数,获得MNIST训练数据集train_loader = load_data('train')# 使用SGD优化器,learning_rate设置为0.01opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())# 训练5轮EPOCH_NUM = 10# MNIST图像高和宽IMG_ROWS, IMG_COLS = 28, 28loss_list = []for epoch_id in range(EPOCH_NUM):for batch_id, data in enumerate(train_loader()):#准备数据images, labels = dataimages = paddle.to_tensor(images)labels = paddle.to_tensor(labels)#前向计算的过程predicts = model(images)#计算损失,取一个批次样本损失的平均值loss = F.square_error_cost(predicts, labels)avg_loss = paddle.mean(loss)#每训练200批次的数据,打印下当前Loss的情况if batch_id % 200 == 0:loss = avg_loss.numpy()[0]loss_list.append(loss)print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, loss))#后向传播,更新参数的过程avg_loss.backward()# 最小化loss,更新参数opt.step()# 清除梯度opt.clear_grad()#保存模型参数paddle.save(model.state_dict(), 'mnist.pdparams')return loss_listmodel = MNIST()
loss_list = train(model)loading mnist dataset from ./work/mnist.json.gz ...... mnist dataset load done epoch: 0, batch: 0, loss is: 25.196237564086914 epoch: 0, batch: 200, loss is: 2.8643529415130615 epoch: 0, batch: 400, loss is: 2.0646779537200928 epoch: 1, batch: 0, loss is: 3.135349988937378 epoch: 1, batch: 200, loss is: 2.058072090148926 epoch: 1, batch: 400, loss is: 2.080343723297119 epoch: 2, batch: 0, loss is: 1.9587202072143555 epoch: 2, batch: 200, loss is: 1.6729546785354614 epoch: 2, batch: 400, loss is: 1.7185478210449219 epoch: 3, batch: 0, loss is: 1.4882879257202148 epoch: 3, batch: 200, loss is: 1.239805817604065 epoch: 3, batch: 400, loss is: 1.5459805727005005 epoch: 4, batch: 0, loss is: 2.2185895442962646 epoch: 4, batch: 200, loss is: 1.598059058189392 epoch: 4, batch: 400, loss is: 1.8100342750549316 epoch: 5, batch: 0, loss is: 1.324904441833496 epoch: 5, batch: 200, loss is: 1.1214401721954346 epoch: 5, batch: 400, loss is: 1.9421234130859375 epoch: 6, batch: 0, loss is: 1.0814441442489624 epoch: 6, batch: 200, loss is: 1.5564398765563965 epoch: 6, batch: 400, loss is: 0.9601972699165344 epoch: 7, batch: 0, loss is: 1.287195086479187 epoch: 7, batch: 200, loss is: 1.1438658237457275 epoch: 7, batch: 400, loss is: 1.0299162864685059 epoch: 8, batch: 0, loss is: 1.0495307445526123 epoch: 8, batch: 200, loss is: 1.5844645500183105 epoch: 8, batch: 400, loss is: 0.9159772992134094 epoch: 9, batch: 0, loss is: 0.8777803778648376 epoch: 9, batch: 200, loss is: 1.1280484199523926 epoch: 9, batch: 400, loss is: 1.1104599237442017
可视化损失变化:
def plot(loss_list):plt.figure(figsize=(10,5))freqs = [i for i in range(len(loss_list))]# 绘制训练损失变化曲线plt.plot(freqs, loss_list, color='#e4007f', label="Train loss")# 绘制坐标轴和图例plt.ylabel("loss", fontsize='large')plt.xlabel("freq", fontsize='large')plt.legend(loc='upper right', fontsize='x-large')plt.show()plot(loss_list)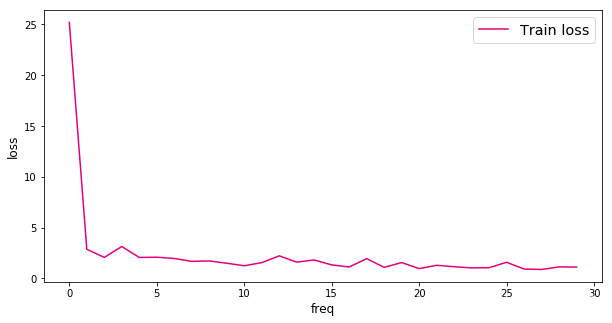
<Figure size 720x360 with 1 Axes>
比较经典全连接神经网络和卷积神经网络的损失变化,可以发现卷积神经网络的损失值下降更快,且最终的损失值更小。
![[牛客复盘] 牛客周赛 Round 9 20230827](https://img-blog.csdnimg.cn/c5c9be61c6534234bc0a2f7927927ee3.png)