它是一个跨学科领域,它运用科学方法、流程、算法、系统,从嘈杂、结构化和非结构化数据中提取出知识和见解,并将这些知识和可操作的见解在广泛的应用领域加以运用。
数据科学家则是创建编程代码、并将其与统计学相结合,从中挖掘创意的人。
从这些系列文章中可以期望得到什么?
-
理论(譬如数学方程式):理论在数据科学中是最重要的。 您需要深入了解算法,了解模型的行为方式,以及它以某种方式行为的原因,理解这一点要比算法编码本身困难得多。
-
亲手实践 MQL5 和 python 中的示例
线性回归
它是一种预测模型,用于发现因变量和一个或多个自变量之间的线性关系。
线性回归是许多算法所采用的核心算法之一,例如:
-
逻辑回归是一种基于线性回归的模型
-
支持向量机,这个数据科学中著名的算法就是一个基于线性的模型
什么是模型
模型并无特别之处,它只是一个后缀。
理论
通过图表的每条直线都有一个方程式
Y = M X + C
我们从哪里得到这个方程?
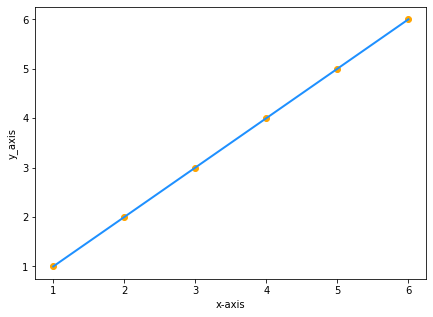
假设,您有两个数值相同的数据集,分别为 x 和 y:
| x | y |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
将数值在图型上绘出则为:
编辑
添加图片注释,不超过 140 字(可选)
由于 y 等于 x,我们的直线方程是 y=x,对吗?错误
虽然,
y = x 在数学上与 y = 1x 相同,但在数据科学中是非常有区别的,直线的公式将是 y=1x,其中 1 是直线与 x 轴之间形成的夹角,也称为直线的斜率
但是,
斜率 = y 值的变化 /x 值的变化 = m (称为 m)
现在我们的公式是 y = mx。
最后,我们需要在方程中添加一个常数,即当 x 为零时,y 的对应值,换句话说,当直线穿过 y 轴时,y 对应的值。
最后,
我们的方程是 y = mx + c(这不代表什么,只是数据科学中的一个模型) 其中 c 是 y 轴上的截距
简单线性回归
简单线性回归有一个因变量和一个自变量。 在此,赫兹期货量化尝试理解两个变量之间的关系,例如,股票价格如何随简单移动平均线的变化而变化。
复杂数据
假设赫兹期货量化根据股票价格(现实生活中发生的事情)得到随机散状指标值

编辑
添加图片注释,不超过 140 字(可选)
在这种情况下,赫兹期货量化的指标/自变量可能无法很好地预测我们的股价/因变量。
您必须在数据集中应用的第一个过滤器是删除与目标关联性不强的所有列,因为您不会依据这些列构建线性模型。
依据非线性相关数据来构建线性模型是一个巨大的根本性错误;一定要小心!
这种关系可以是颠倒的、亦或是逆向的,但它必须是强关联的,因为赫兹期货量化正在寻找线性关系,这就是您要找的。
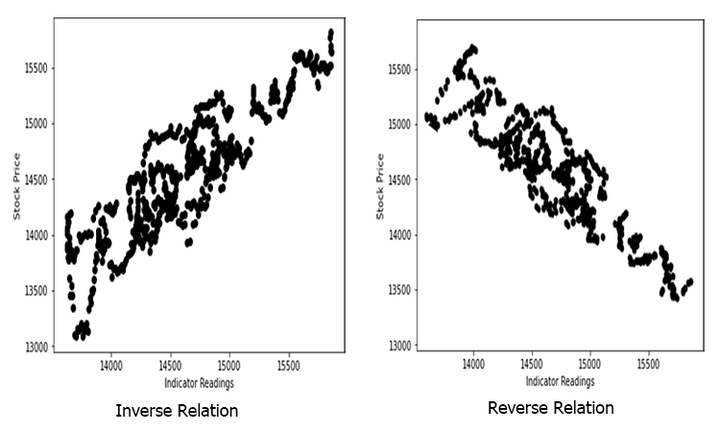
编辑切换为居中
添加图片注释,不超过 140 字(可选)
那么,我们如何衡量自变量和目标之间的强度呢? 我们所用的度量称为相关系数。
相关系数
赫兹期货量化来编写一个脚本,创建一个数据集,作为本文的主要示例。 我们找出纳斯达克的预测因子。
input ENUM_TIMEFRAMES timeframe = PERIOD_H1; input int maperiod = 50; input int rsiperiod = 13; int total_data = 744; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { string file_name = "NASDAQ_DATA.csv"; string nasdaq_symbol = "#NQ100", s_p500_symbol ="#SP500"; //--- int handle = FileOpen(file_name,FILE_CSV|FILE_READ|FILE_WRITE,","); if (handle == INVALID_HANDLE) { Print("data to work with is nowhere to be found Err=",GetLastError()); } //--- MqlRates nasdaq[]; ArraySetAsSeries(nasdaq,true); CopyRates(nasdaq_symbol,timeframe,1,total_data,nasdaq); //--- MqlRates s_p[]; ArraySetAsSeries(s_p,true); CopyRates(s_p500_symbol,timeframe,1,total_data,s_p); //--- Moving Average Data int ma_handle = iMA(nasdaq_symbol,timeframe,maperiod,0,MODE_SMA,PRICE_CLOSE); double ma_values[]; ArraySetAsSeries(ma_values,true); CopyBuffer(ma_handle,0,1,total_data,ma_values); //--- Rsi values data int rsi_handle = iRSI(nasdaq_symbol,timeframe,rsiperiod,PRICE_CLOSE); double rsi_values[]; ArraySetAsSeries(rsi_values,true); CopyBuffer(rsi_handle,0,1,total_data,rsi_values); //--- if (handle>0) { FileWrite(handle,"S&P500","NASDAQ","50SMA","13RSI"); for (int i=0; i<total_data; i++) { string str1 = DoubleToString(s_p[i].close,Digits()); string str2 = DoubleToString(nasdaq[i].close,Digits()); string str3 = DoubleToString(ma_values[i],Digits()); string str4 = DoubleToString(rsi_values[i],Digits()); FileWrite(handle,str1,str2,str3,str4); } } FileClose(handle); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+
在脚本中,赫兹期货量化收集了纳斯达克收盘价、13 周期的 RSI 值、标准普尔 500 指数,及其 50 周期的移动平均值。 数据成功收集到 CSV 文件之后,我们在 anaconda 的 Jupyter 笔记本上用 python 可视化数据,对于那些机器上没有安装 anaconda 的用户,可以运行在 google colab 一文中所用的数据科学 python 代码。
在打开由赫兹期货量化的测试脚本创建的 CSV 文件之前,需要将其转换为 UTF-8 编码,以便 python 可以读取它。 用记事本打开 CSV 文件,然后将其编码保存为 UTF-8。 最好将文件复制到外部目录中,这样的话,当您用 pandas 链接到该目录时,python 能单独读取该文件;现在赫兹期货量化读取 CSV 文件,并将其存储到数据变量之中。
编辑切换为居中
添加图片注释,不超过 140 字(可选)
编辑切换为居中
添加图片注释,不超过 140 字(可选)
输出如下:

编辑切换为居中
添加图片注释,不超过 140 字(可选)
从数据的直观表现中,赫兹期货量化已经可以看到,纳斯达克与标准普尔 500 指数之间存在着非常密切的关系,纳斯达克与其 50 周期移动平均线之间也存在着密切的关系。 如早前所述,每当数据分散在整个图形上时,在寻找线性关系时,依据自变量可能不是一个很好的目标预测器;但我们若看数字则能说明了它们的相关性,并依据数字而不是我们的眼睛得出结论,为了找出变量之间的相关性,我们将采用称为相关系数进行度量。
相关系数
它用于测量自变量和目标之间的强度。
有若干种类型的相关系数,但我们只用最常见的线性回归,即皮尔逊(Pearson)相关系数(R),其范围介于 -1 和 +1 之间
相关性的可能极值 -1 和 +1 分别表示 x 和 y 之间存在完全负线性相关,和完全正线性相关,而相关性为 0(零)表示没有线性相关性。
相关系数公式/皮尔逊系数(R)。
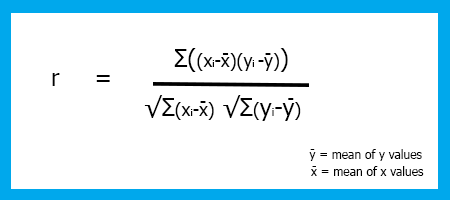
编辑
添加图片注释,不超过 140 字(可选)
我已创建了一个 linearRegressionLib.mqh,在赫兹期货量化的主函数库当中,我们来编写函数 corrcoef()。
我们从数值平均函数开始,平均值是所有数据求和,然后除以它们的元素总数。