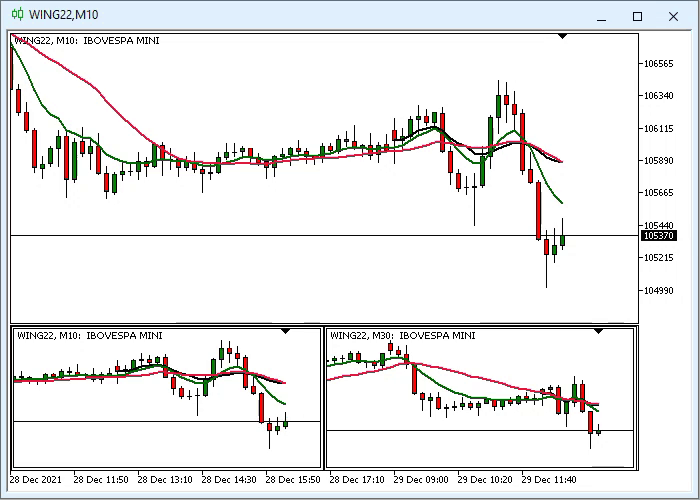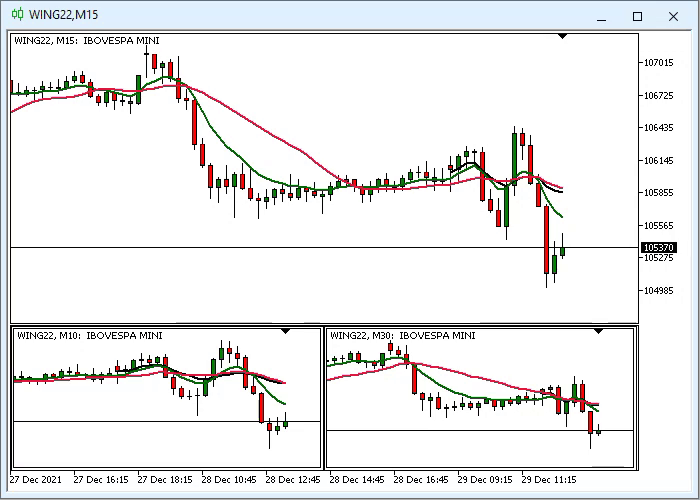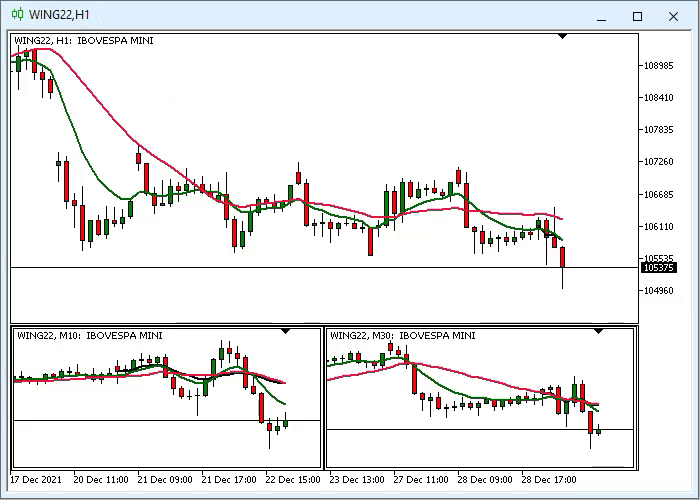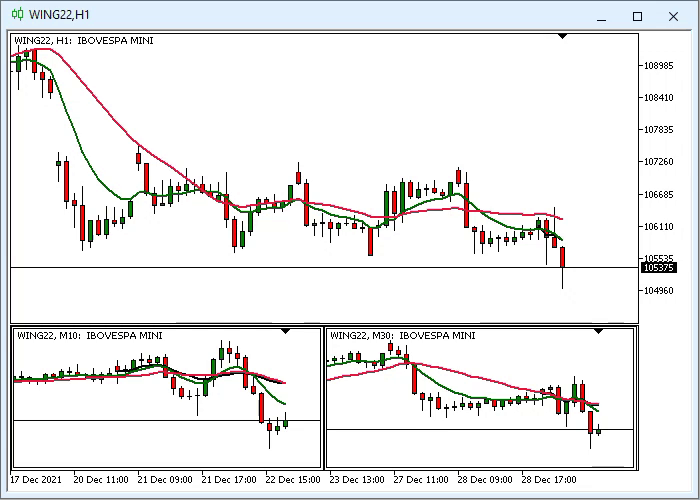
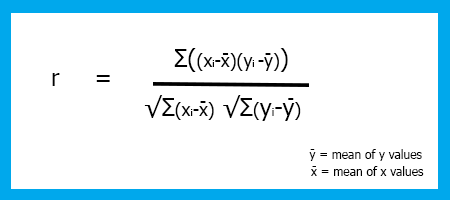期货量化软件：衡量指标信息

机器学习依靠数据训练来学习市场的一般行为，最终做出相当准确的预测。所选学习算法必须遍历精心挑选的样本，以便提取有意义的信息。许多人未能成功应用这些精密工具的原因是，大多数有意义的信息都隐藏在嘈杂的数据当中。对于许多策略开发人员来说可能并不清楚，他们选取的数据集可能不适合模型训练。

指标可考虑作为针对基础价格序列携带有关信息的提供者。利用这个前提，熵可以用来衡量指标传达了多少信息。使用 Timothy Masters 撰写的《测试和优调市场交易系统（TTMTS）》一书中记录的步骤和工具，赫兹期货量化来演示如何使用这些步骤和工具来评估指标数据的结构。

为什么要衡量指标信息

通常，在使用机器学习工具进行策略开发时，赫兹期货量化只是简单地将各种数据扔给算法，希望能从中得到一些结果。最终的成功将取决于模型中所用的预测变量的品质，且有效的预测因子通常具有某种特征。其中之一充满了重要的信息内容。

在模型训练的变量中信息量很重要，但并不是有效模型训练的唯一要求。因此，衡量信息内容可在训练过程中筛选盲目选用的指标。

熵

在赫兹期货量化上撰写有关熵的文章已有很多次了。我要向读者们道歉，因为他们将不得不忍受另一个定义，但我保证这对于理解该概念的应用至关重要。之前的文章已经提供了熵计算的历史和推导，所以为了简洁起见，我们直接从方程开始。

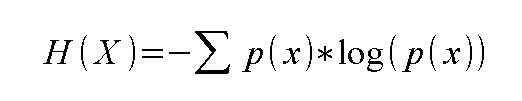
编辑

添加图片注释，不超过 140 字（可选）

H(X) 表示 X 的熵，X 是表示任意变量的离散变量，例如一条消息。消息的内容只能假定有限数量的值。这在等式中表示为小写的 x。小写 x 是消息的观测值，如此，如果 x 的所有可能值都可在一个集合 N 中列举。

研究一个公平骰子的例子。掷骰子时，可以被视为提供信息，判定游戏的结果。骰子有 6 条独特的边，编号为 1 到 6。观察到任何朝上的数字的概率是 1/6。

依此示例，大写 X 是骰子，小写 x 可以是骰子侧面绘制的任何数字。所有这些都置于集合 N ={ 1,2,3,4,5,6}。应用公式，这个骰子的熵是 0.7781。

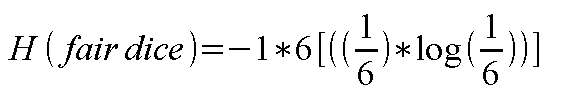
编辑

添加图片注释，不超过 140 字（可选）

现在考虑另一个骰子，它有制造缺陷。它有 2 个面，上面画着相同的数字。对于这个有缺陷的骰子，集合 N 的可能值是 {1,1,3,4,5,6}。再次使用该公式，赫兹期货量化得到的平均熵值为 0.6778。

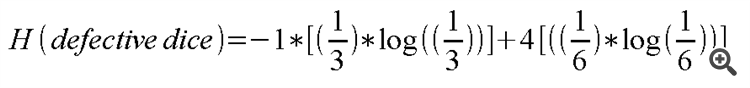
编辑切换为居中

添加图片注释，不超过 140 字（可选）

比较这些值，赫兹期货量化注意到信息内容减少了。分析两个骰子，当观察每个可能值的概率都相等时，熵方程产生其最大可能值。因此，当所有可能值的概率相等时，熵达到其最大平均值。

如果我们丢弃有缺陷的骰子，作为产生传统实数输出的指标。那么，X 成为指标，小写 x 则将是指标可以承担的数值范围。在继续之前，赫兹期货量化遇到了一个问题，因为熵方程严格处理离散变量。变换方程操控连续变量是可能的，但是这样应用是困难的，故此坚持离散数的领域更容易。

计算指标的熵

若要将熵方程应用于连续变量，赫兹期货量化必须指标的值离散化。这是通过将数值范围划分为大小相等的区间，然后计算落入每个区间的数值个数来完成的。使用这种方法，枚举指标所有值的最大范围的原始集合被被子集替换，每个子集都是选定的区间。

在处理连续变量时，可以依据变量假设概率变化的可能值，因为它显然为熵应用于指标提供了一个重要的方面。

回到抛骰子的第一个例子。如果赫兹期货量化将最终熵值的每一个除以各自熵 n 的 log(N)。第一个骰子产生 1，而有缺陷的骰子产生 0.87。将熵值除以变量数值个数的对数，可以假设产生的度量对应于变量的理论最大熵。其可称为比例或相对熵。

正是这个数值，在赫兹期货量化评估指标时起到大用，因为该指标能示意熵与其理论最大平均值的接近程度。它越接近最大值那一侧越好，而指标另一个端点的任何内容也许是暗示，在任何类型的机器学习尝试中，该指标都只是一个劣等候选者。

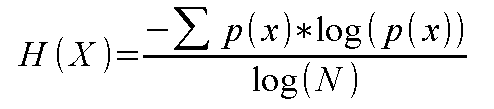
编辑

添加图片注释，不超过 140 字（可选）

最终应用的等式如上所示，代码在下面以赫兹期货量化脚本实现，可在文章末尾的附件里下载。使用该脚本，赫兹期货量化就能够分析大多数指标。

计算指标熵的脚本

用户调用脚本时可调整以下参数：

TimeFrame - 选定分析指标值的时间帧。
IndicatorType - 用户可在此选择一个内置指标进行分析。若要指定自定义指标，请选择自定义指标选项，并在下一个参数值中输入指标名称。
CustomIndicatorName - 如果上一个参数选择了自定义指标选项，则用户必须在此处输入正确的指标名称。
UseDefaults - 如果设置为 true，将使用指标中的硬编码作为默认的用户输入。
IndicatorParameterTypes - 这是以逗号分隔的字符串，必须按照正确顺序列出指标的数据类型 — 一个可能的输入示例，假设要分析的指标分别接受 4 个输入：双精度、整数、整数、字符串类型；用户只需输入 “double, integer, integer, string”，也支持缩写形式 “d, i, i, s”，其中 d= double，i=integer 以及 s=string。列举值映射为整数类型。
IndicatorParameterValues - 与前面的输入一样，这也是一个以逗号分隔的数值列表，例如，使用前面的示例 “0.5, 4, 5, string_value”。如果指标参数值或指标参数类型的参数格式有任何错误，将导致指标的默认值无法破译，或丢失。检查智能系统，以便获取错误消息。请注意，此处无需包含指标名称，如果考虑自定义指标，则必须由 CustomIndicatorName 指定。
IndicatorBuffer - 用户可以规定要分析的指标缓冲区编号。
HistoryStart - 历史记录样本的开始日期。
HistorySize - 相对于历史开始要分析的柱线数量。
Intervals - 此参数指示为离散化过程创建的编号间隔。 TTMTS 的作者为几千个样本量指定了 20 个区间，其中 2 个被规定为硬性最小值。我已在相应的数值上添加了自己的数值转轮，则相对于样本大小实现了改变区间数的可能性，特别是每 1000 个样本可划分 51 个。如果用户输入的任何值小于 2，则此选项可用。故此，需要明确的是，将区间设置为任何小于 2 的数字，使用的区间数量将根据所分析的柱线数量而变化。

//--- input parameters input ENUM_TIMEFRAMES Timeframe=0; input ENUM_INDICATOR IndicatorType=IND_BEARS; input string CustomIndicatorName=""; input bool UseDefaults=true; input string IndicatorParameterTypes=""; input string IndicatorParameterValues=""; input int IndicatorBuffer=0; input datetime HistoryStart=D'2023.02.01 04:00'; input int HistorySize=50000; input int Intervals=0; int handle=INVALID_HANDLE; double buffer[]; MqlParam b_params[]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { if(!processParameters(UseDefaults,b_params)) return; int y=10; while(handle==INVALID_HANDLE && y>=0) { y--; handle=IndicatorCreate(Symbol(),Timeframe,IndicatorType,ArraySize(b_params),b_params); } //--- if(handle==INVALID_HANDLE) { Print("Invalid indicator handle, error code: ",GetLastError()); return; } ResetLastError(); //--- if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0) { Print("error copying to buffer, returned error is ",GetLastError()); IndicatorRelease(handle); return; } //--- Print("Entropy of ",(IndicatorType==IND_CUSTOM)?CustomIndicatorName:EnumToString(IndicatorType)," is ",relativeEntroy(Intervals,buffer)); //--- IndicatorRelease(handle); } //+------------------------------------------------------------------+ //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool processParameters(bool use_defaults,MqlParam &params[]) { bool custom=(IndicatorType==IND_CUSTOM); string ind_v[],ind_t[]; int types,values; if(use_defaults) types=values=0; else { types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t); values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v); } int p_size=MathMin(types,values); int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size); if(custom) { params[0].type=TYPE_STRING; params[0].string_value=CustomIndicatorName; } //if(!p_size) // return true; if(use_defaults) return true; int i,z; int max=(custom)?values_to_input-1:values_to_input; for(i=0,z=(custom)?i+1:i; i<max; i++,z++) { if(ind_t[i]=="" || ind_v[i]=="") { Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters"); break; } params[z].type=EnumType(ind_t[i]); switch(params[z].type) { case TYPE_INT: params[z].integer_value=StringToInteger(ind_v[i]); break; case TYPE_DOUBLE: params[z].double_value=StringToDouble(ind_v[i]); break; case TYPE_STRING: params[z].string_value=ind_v[i]; break; default: Print("Error: Unknown specified parameter type"); break; } } return true; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ ENUM_DATATYPE EnumType(string type) { StringToLower(type); const ushort firstletter=StringGetCharacter(type,0); switch(firstletter) { case 105: return TYPE_INT; case 100: return TYPE_DOUBLE; case 115: return TYPE_STRING; default: Print("Error: could not parse string to match data type"); return ENUM_DATATYPE(-1); } return ENUM_DATATYPE(-1); } //+------------------------------------------------------------------+

只需注意为间隔选择的值：更改计算中使用的间隔数，将改变最终熵值。在进行分析时，明智的做法是保持某种一致性，以尽量减少所使用的独立输入的影响。在脚本中，相对熵计算封装在 Entropy.mqh 文件中定义的函数之中。

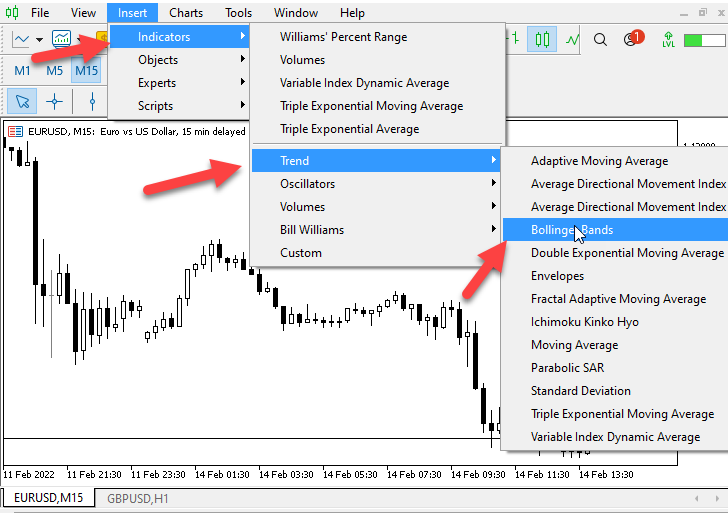
该脚本只是在智能系统选项卡中打印生成的熵值。很对各种内置和自定义指标运行脚本，会产生如下所示的结果。有趣的是，威廉的百分比范围具有接近完美的相对熵。将其与市场促进指数指标进行比较，后者显示令人失望的结果。