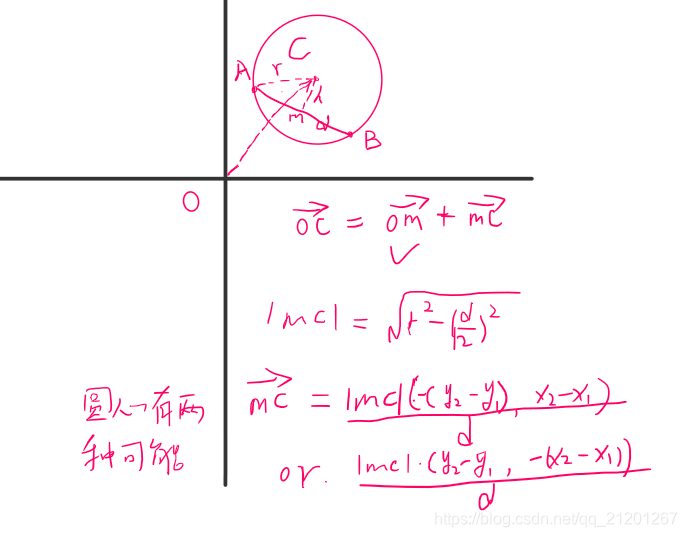模拟题

红靶子的我们先不考虑。

如果是 {1,2,2} ， {2,2,3} 这种只涉及两种倍数的话，我们想到不定方程：

ax+by =c 的通解形式（a,b,c 为常数），从而探讨 x,y 在规定取值内是否有解。

探讨 {1,2,3} 的情况。

这个时候不难发现 $x\in [1,6k]$ 是有解的。

如果你暴力每种情况枚举的话会比较麻烦。

我们可以递归求解：（当然这是个笨方法）

对于轮数为 1 的情况相对较少，直接求解。

对于轮数等于 2 的情况，有几种情形：

第一种，有一个为 M 的靶

第二种，有一个为 2M 的靶

第三种，没有红心靶

组合形式为

{2,2}, {1,2} , {2,3}

如果之前有过 2M 的靶，还可以是：

{3,3} , {1,3}

对于轮数等于 3 的情况，有几种情形：

第一种，有一个为 M 的靶

第二种，有一个为 2M 的靶

第三种，没有红心靶

组合形式为

{1,2,3} , {2,2,3} , {2,3,3}

讲一下这个不定方程到底怎么求。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
//贪心
int T, res;
ll A1, B1, C1, D1, K1;
ll A2, B2, C2, D2, M1;
ll A3, B3, C3, D3, X1;
bool check(ll X, ll Y, ll M) {ll l = -M - 3 * floor((X - M) / 2.0), r = -M - 3 * ceil((1 - M) / 2.0);if (r >= 1 && l <= Y) {return 1;}return 0;
}
bool solve(int k, ll K, ll M, ll X, int limit) {if (X == 0) {return (limit == 1);}if (k == 1) {if (X == 2 * M || (X % 2 == 0 && X / 2 <= K)) {return 1;}if (limit) {if (X <= K || (X % 3 == 0 && X / 3 <= K) || X == M) {return 1;}}return 0;}if (X >= M && solve(k - 1, K, M, X - M, limit))return 1;if (X >= 2 * M && solve(k - 1, K, M, X - 2 * M, 1))return 1;if (solve(k - 1, K, M, X, limit))return 1;if (k == 2) {if (X % 2 == 0 && X / 2 <= 2 * K)return 1;if (X > 1 && X <= 3 * K)return 1;if (check(K, K, X))return 1;if (limit) {if (X % 3 == 0 && X / 3 <= 2 * K)return 1;if (X <= 4 * K)return 1;}return 0;}if (k == 3) {if (X <= 6 * K)return 1;if (check(2 * K, K, X) || check(K, 2 * K, X))return 1;return 0;}return 0;
}
int main() {//  freopen("data.in","r",stdin);//  freopen("dart.in","r",stdin);//  freopen("dart.out","w",stdout);scanf("%d", &T);scanf("%lld%lld%lld%lld%lld", &A1, &B1, &C1, &D1, &K1);scanf("%lld%lld%lld%lld%lld", &A2, &B2, &C2, &D2, &M1);scanf("%lld%lld%lld%lld%lld", &A3, &B3, &C3, &D3, &X1);//  solve(3,20,32,205,0);res += solve(3, K1, M1, X1, 0);for (int i = 2; i <= T; i++) {K1 = (((__int128)A1 * K1 * K1 + B1 * K1 % D1 + C1) % D1) + 20;M1 = (((__int128)A2 * M1 * M1 + B2 * M1 % D2 + C2) % D2) + 20;X1 = (((__int128)A3 * X1 * X1 + B3 * X1 % D3 + C3) % D3) + 20;res += solve(3, K1, M1, X1, 0);//      if(solve(3,K1,M1,X1,0)) {//          printf("%lld %lld %lld\n",K1,M1,X1);//      }}printf("%d", res);
}
// 20 32 205
//1
//0 0 0 0 100
//0 0 0 0 1000
//0 0 0 0 1001