LeetCode 1453. 圆形靶内的最大飞镖数量（几何题）

1. 题目

墙壁上挂着一个圆形的飞镖靶。现在请你蒙着眼睛向靶上投掷飞镖。

投掷到墙上的飞镖用二维平面上的点坐标数组表示。飞镖靶的半径为 r 。

请返回能够落在任意半径为 r 的圆形靶内或靶上的最大飞镖数。

示例 1：
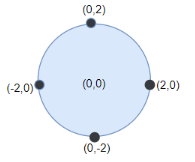
在这里插入图片描述

输入：points = [[-2,0],[2,0],[0,2],[0,-2]], r = 2
输出：4
解释：如果圆形的飞镖靶的圆心为 (0,0) ，半径为 2 ，
所有的飞镖都落在靶上，此时落在靶上的飞镖数最大，值为 4 。

示例 2：
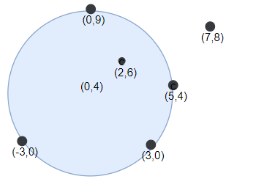
在这里插入图片描述

输入：points = [[-3,0],[3,0],[2,6],[5,4],[0,9],[7,8]], r = 5
输出：5
解释：如果圆形的飞镖靶的圆心为 (0,4) ，半径为 5 ，
则除了 (7,8) 之外的飞镖都落在靶上，此时落在靶上的飞镖数最大，值为 5 。示例 3：
输入：points = [[-2,0],[2,0],[0,2],[0,-2]], r = 1
输出：1示例 4：
输入：points = [[1,2],[3,5],[1,-1],[2,3],[4,1],[1,3]], r = 2
输出：4提示：
1 <= points.length <= 100
points[i].length == 2
-10^4 <= points[i][0], points[i][1] <= 10^4
1 <= r <= 5000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-number-of-darts-inside-of-a-circular-dartboard
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

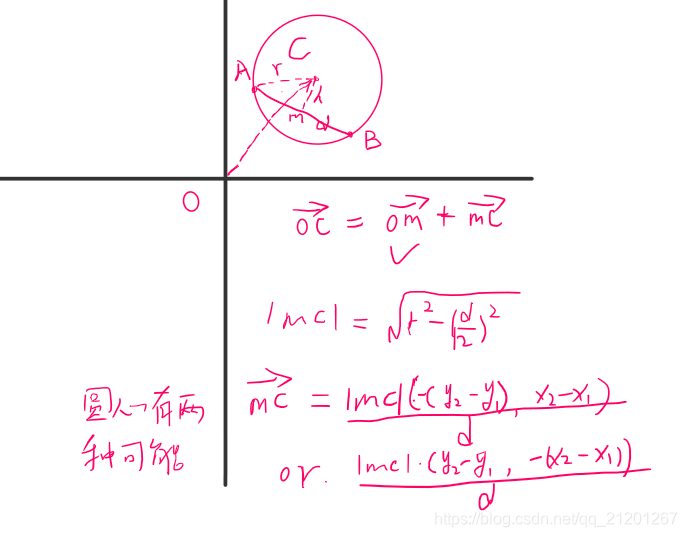
在这里插入图片描述

class Solution {double cx, cy;//圆心坐标
public:int numPoints(vector<vector<int>>& points, int r) {int x1, x2, y1, y2;double dx, dy;int i, j, k, count, maxcount=1, n = points.size();for(i = 0; i < n; ++i){x1 = points[i][0];y1 = points[i][1];for(j = i+1; j < n; ++j)//i,j为圆上的点{if(i == j)continue;x2 = points[j][0];y2 = points[j][1];count = 2;int d_d = (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);if(d_d > 4*r*r) continue;count = 0;cx = (x1+x2)/2.0-(y2-y1)*sqrt((r*r-d_d/4.0)/d_d), cy = (y1+y2)/2.0+(x2-x1)*sqrt((r*r-d_d/4.0)/d_d);for(k = 0; k < n; ++k){dx = points[k][0]-cx;dy = points[k][1]-cy;if(dx*dx+dy*dy <= r*r)count++;}maxcount = max(maxcount, count);count = 0;cx = (x1+x2)/2.0+(y2-y1)*sqrt((r*r-d_d/4.0)/d_d), cy = (y1+y2)/2.0-(x2-x1)*sqrt((r*r-d_d/4.0)/d_d);for(k = 0; k < n; ++k){dx = points[k][0]-cx;dy = points[k][1]-cy;if(dx*dx+dy*dy <= r*r)count++;}maxcount = max(maxcount, count);}}return maxcount;}
};