图像压缩基础

1)压缩的原因:数字视频码率高达216Mb/s。数据量之大，无论是网络传输，还是存储都构成巨大压力。在保持信号质量的前提，要降低码率及数据量。
2)压缩的原理: 图像信息存在着大量的规律性或相关性，在传输的前一个样值中包含了后一个样值或后一帧中相关位置的样值内容。

3)压缩的目标:①去除信息中的相关性，去除冗余码，使样值独立，降低信息码流。②可以采用一些特殊的编码方式，使平均比特数降低，从而可进一步降低信息流码流。信源编码: 降低码率的过程，称为压缩编码，也叫信源编码。

4)压缩方法：编码方式是多种多样的，不同的算法其压缩率也不同，但都应本着无损的原则。在实际应用中往往是采用多种不同算法的综合缩编码方式，反复压缩，以取得较高的压缩率。

压缩编码基础---莫尔斯码

电报码:是采用“· ”和“”—”来表示26个英文字母的变字长编码。

编码思想:(1) 常用字母用短码表示。(2) 不常用的字母用长码表示。
编码方法：通过变字长编码方式。对常用英文单词进行的大量统计。找出各字母出现的概率，最后确定:12个字母（出现几率最小）用4bit数字表示；8个字母（出现几率较少的）用3bit数字表示；4个字母（出现几率较高的）用2bit字示数字表示；2个字母（出现几率最高的）用1bit数字表示，共26字母。

出现几率最低的12个字母共需 12×4bit=48bit
出现几率较低的8字共个字母共需   8×3bit=24bit
出现几率较高的4字共个字母共需    4×2bit=8bit
出现几率最高的2字共个字母共需    2×1bit=2bit
结论：
每个字母的平均码长为:
      平均码长=(48+24+8+2)÷26=3.15bit/字母

讨论：
    (1)要用固定码长方式则需要25 =32,即5bit
来表示。
    (2)莫尔斯码编码规律：先找出统计规律，然后对出现概率大的用短码，反之用长码。
    (3)压缩对信息质量的影响: 而这种压缩对信息无任何损坏，属无损压缩。

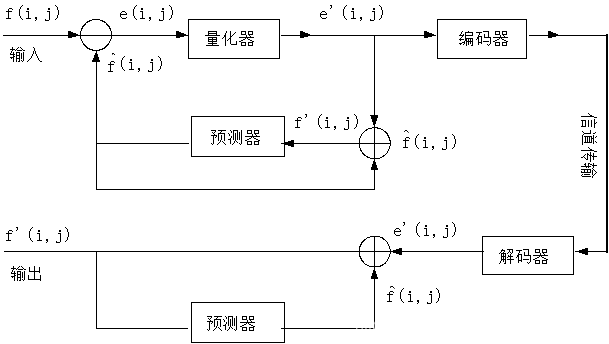
压缩编码基础—预测编码

差值编码原理
样值与前一个（相邻）样值的差值，则这些差值绝大多数是很小的或为零，可以用短
码来表示，而对那些出现几率较少的较大差值，用长码来表示，则可使总体码数下降。
采用对相邻样值差值进行变字长编码的方式称为差值编码，又称为差分脉码调制（PMDPCM）

霍夫曼(Huffmun)码

（1）变字长编码：对信源中出现概率大的“对象”用短码表示，对出现概率较小的“对象”用长码表示。其可获得较短的平均码长。
注： “对象” 只是一个欲编码的数据、符号或元素。

①将信源对象按出现的概率由大到小排序。
②找出最小两个概率点，大为“”1”，小为“”0”，如概率相等，随意“”0”和“”1”分配。
③将这两个概率点的概率相加，生成一新概点的概率点。

④再在新生成概率点与余下概率点中再选两个最小比较，大为“”1”小，小为“”0”。
⑤再求和，生成一新的概率点，以此类推，直至新的概率点的概率为1为止。
⑥最后将对应各“对象”的数码，按结构顺序组合起来，即为各信源“对象”的霍夫曼码编码。

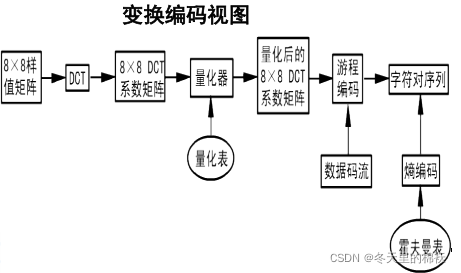
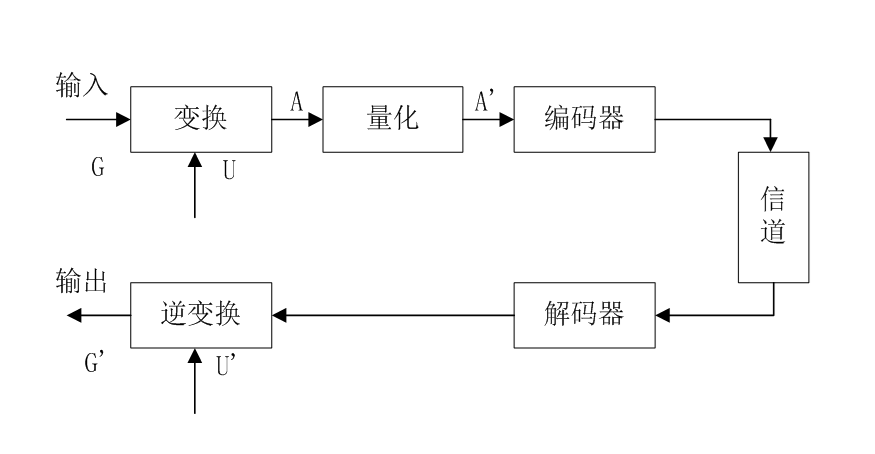
压缩编码基础—变换编码

(1)变换的原因：信号的相关性不仅表现在位置空间（空域）中，在其他的域(频域)中也具有很强的相关性，因此压缩编码的方法并不唯一。
(2)不同域有不同特点：静止图像的位置相关性较强，运动图像的频率相关性较强，因此在空域中解决不了的问题在频域中就可以解决。

压缩编码基础—离散余弦变换（DCT）

(1)图像的频率特征：低频信号幅值大，高频信号幅值小。信号能量主要集中于低频量分量,高频分量的能量较小。
(2)相关性分析：将信号变换到频率域中，幅值大的低频分量集中在一个区域，幅值小的高频分量分布在其他位置，表现出了较强的频率相关性。DCT编码就是这种效率更高，便于压缩的编码方法。

①分块：将每个分量图像分成许多8×8=64个样点组成的像块，得到在空域中的8×8的样值矩阵。
②变换：利用FDCT公式，将空域中的×8×8样值矩阵，正向变换为频域中的8×8 DCT系数矩阵。

F（0，0）对应直流分量，称为DC系数，其它63个对应交流分量的系数，称为AC系数。

两个空间的同位置系数无对应关系。在频域中的右下角对应高频部分，而在左上角对应低频部分（特点，相关性）。DC系数为空域中64样值的平均值。

AC系数构成：

当u，v≠0，时，C（U）=C（V）=1，每个AC系数为空域中64个样值分别乘以对应的余弦量后求和，再取平均。

DCT系数规律：低频系数值大，高频系数值小。
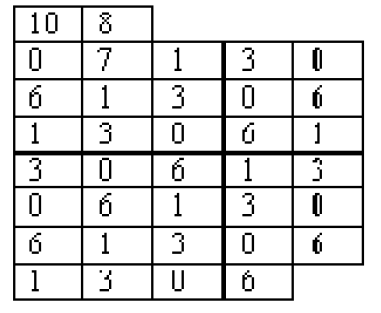
对比两个数值矩阵观察相关性

变换编码矩阵

IDCT变换（逆变换）：DCT系数并不能重构图像，因此需要利用IDCT公式将频域中的8×8
DCT系数矩阵变换为空域中的8×8样值矩阵，使图像得以还原。

逆向DCT变换（IDCT）：

DCT系数量化
量化的原因：DCT之后其系数矩阵中相关性不够明显，为进一步降低DCT系数矩阵中非零系数的
幅值，增加零系数的个数，使相关性表现的更明显，需要进一步量化。

量化的依据：①对失真的要求：量化是图像质量下降的重要原因，DCT系数量化是基于限失真编码理论进行的，容许有失真，但应在视觉容许的容限内。
②视觉要求：
      . a. 对亮度信号与色度信号的分辨能力不同;
      . b. 对低频图像信号和高频图像信号的分辨能力不同。
      结论：可以采用不同的量化方案。

压缩编码基础—量化

量化的方法：

区域滤波法：
对DCT系数矩阵中的每一个值逐一量化。
F(U，V)为DCT系数矩阵中位于(U，V)的DCT系数;
W(U，V)为量化表中位于(U，V)点的量化步长，（不同位置可以采用不同的量化步长）;
Q(U，V)对应于U(U，V)位置的量化值。
round（）为取整函数。

讨论：
a.量化表的区域性：DCT系数矩阵中不同的区域采用不同的量化步长（高低频的区别）

b.量化表的多样性：对不同的分量信号采用不同的量化表（不同分量信号的区别）

c.量化表的可变性：是比较理想的，还可以改变。

区域滤波法：属于均匀量化方式（对每点而言）。
信号数字化中的量化与DCT系数量化的区别：前者为描述信号幅值，后者降低信号幅度。
逆量化Q-1：接收端，一定要使用与发送端相同的量化表进行逆量化，方可使图像还原。

视觉加权法：采用统一的量化步长，再配以8×8视觉加权矩阵，其中对应于DC的权值最高
为1。而对应于AC的权值都小于1，对应于高频的权值为最小。
视觉加权的量化方案采用下列公式：

式中W为统一步长，K(U，V)加权系数。

压缩编码基础—Zig-Zag扫描

Zig-Zag扫描：一种将二维数组转变为一维数组的Z字形扫描方法。
   (1)采用扫描的原因：量化后的DCT系数仍然是二维系数矩阵，无法直接传输，还需将其变为一维据序列。对Q矩阵重新排列。
   (2)Zig-Zag扫描的依据：在量化后的DCT系数矩阵中，非0的数据主要都集中于矩阵的左上角。
   (3) Zig-Zag扫描的方法：Zig-Zag扫描采用的是Z字形扫描方式。从直流分量DC开始进行Z形描字形扫描。

(4)Zig-Zag扫描序列：系数矩阵Q，进行Zig-Zag扫描所得到的数据序列。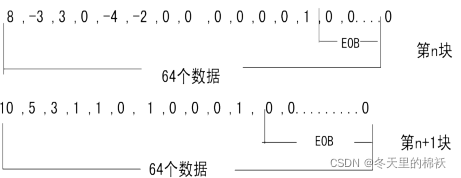

(5)Z扫描的特点
①可以增加连续0系数的个数，也就是增加0游程长度。
②在数据序列中，非零系数主要都集中于数据序列的首部，在数据序列的尾部，则都是连
零(EOB)数据。这样对传输中的数据压缩十分利有利。

压缩编码基础—游程编码 (RLC)

游程编码 (RLC):消去一维数组序列尾部连续0数据的编码方法。

1)游程：连续0的长度，或连续0的个数。
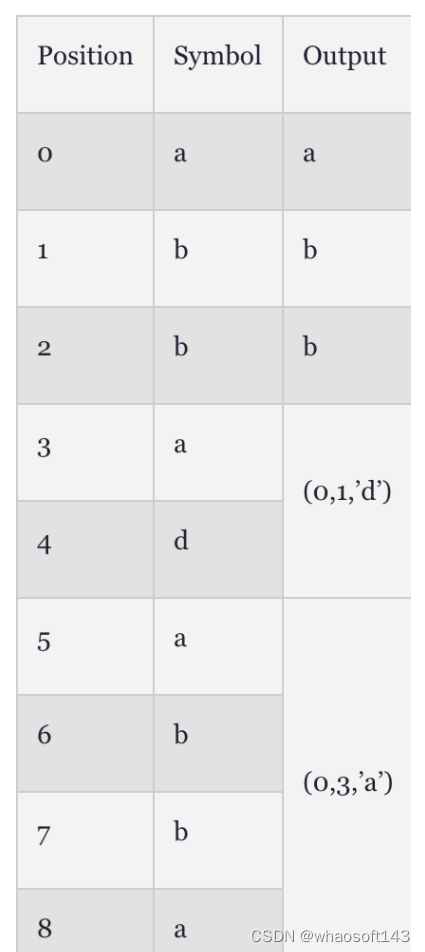
2)游程编码的方法：将一维数组序列转化为一个由二元数组(run,level)组成的数组序列。
其中：①run示续表示连续0的长度；
②level表示连续0后的一个非零值；
③用EOB表示后面所有剩余的连续0。

3)游程编码实例（10进制）：对应以上的两个一维数组序列的游程编码为：
(0,8), (0,-3)，(0,3)，(1,-4)，(0,-2)，(6,1)，EOB 第n块
(0,10), (0,5)，(0,3)，(0,1)，(0,1)，(1,1)，(3,1)，EOB 第n+1块

4)16进制的编码方法：每两个字节为一个字符对。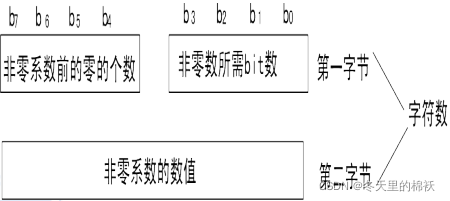

注：①第一字节中：高4位表示一维数组序列中非零系数前零的个数。低4位则表示这个非零系
数所需的比特数。
     ②第二字节：完全用于表示非零系数的数值。
     ③ EOB 用FFFF表示。
     ④负数在此用补码表示。

(0,8), (0,-3)，(0,3)，(1,-4)，(0,-2)，(6,1)，EOB 第n块
(0,10), (0,5)，(0,3)，(0,1)，(0,1)，(1,1)，(3,1)，EOB 第n+1块

因此上数组序列又可表示为：04,08，08,FD， 02,03, 18,FC，08,FE，61,01，FFFF(H) 第n块字符对组
04,0A，03,05，02,03，01,01，01,01，11,01，31,01，FFFF(H) 第n+1块字符对组
5)解码：在解码时见到FFFF就自动补0一直补足64个数据为止。

压缩编码基础—熵编码