图像编码算法尽可能节省图像的存储空间和减少传输带宽需求，图像编码的目的是在满足一定解码重构质量的条件下利用尽可能少的比特数对图像进行表示。数字图像中的像素都不是独立存在的，小到相邻像素之间，大到图像块与图像块之间，不同的图像之间，都会存在一定的相关性。从信息论的角度来说，数据之间的相关性意味着互信息的存在，因此会造成信息上的冗余，而冗余的存在就为图像编码提供了可能。

传统视频图像压缩技术都是基于离散余弦变换（DCT）的压缩方法，例如国际的 H.264 、MPEG4、JPEG  等压缩标准都采用了该技术。DCT是利用对图像分块来进行图像变换的，无法消除块边间的相关性，因此，会出现一些影响我们视觉效果的方块效应，尤其是在低比特率的情下。而近几十年来发展起来的小波变换以其内在的多尺度分析结构很好的解决了因离散余弦变换所导方块效应，小波变换在时/频域均具有良好的局部化特征，能在不同尺度上对视频图像信号进行细化分析，从而抽取信息中的关键信息。通常，一幅典型的图像主要是由包含低频信息的变换缓慢的齐次区域和既包含高频信息又包含部分低频信息的纹理区域以及相当少的包含绝大部分高频信息的变换剧烈的视觉敏感边界组成的。而小波变换则可在将其高低频信息隔开的同时将绝大部分能量压缩到低频子带中，从而达到减小空间冗余的目的。由于其独特的内在特性有着重要的理论与应用研究价值，被很多学者认为是提高视频图像压缩效率的关键。

目前，基于小波变换的静态图像压缩算法主要有 EZW 算法，SPIHT 算法和 EBCOT
算法。

通常对于静态图像压缩的一般步骤主要分为小波变换、量化、系数编码和熵编码几个部分。变换过程会获得一个小波系数矩阵；量化是根据人眼视觉特性，降低精度将小波系数量化为有限的字母表并且不可逆的一个过程；编码是将量化之后得到的符号进行进一步压缩以实现最小化比特率。而在实际压缩编码中，根据不同需求，量化、系数编码和熵编码中的某步骤可能会被合并或省略，但其本质思路是一致的，解码是其编码的逆向过程。

根据原始数据是否有损失，图像编码可以分为有损编码和无损编码。

无损编码是一种没有任何信息损失的编码，因此，将编码后的数据进行解码，得到的重构图像与原图像是完全一致的。虽然无损编码可以完全保留原图像的信息，但其压缩效率比较有限。

为了进一步提升压缩效率，有损编码应运而生。虽然在有损编码后，重构图像与原图像相比存在一定的重构误差，但是这种编码方式却能大幅度的提高压缩比，并且，一定程度的信息损失是可以被人眼所接受的，因此，目前大部分的图像编码采用的都是有损编码的方式。

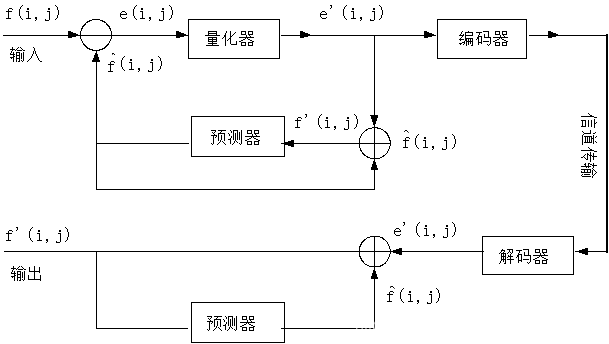
完整的图像压缩编码可以分为编码和解码两大过程。

编码过程通过一定的方法将输入图像的数据表示为二进制码流，并同时完成数据的压缩。这一过程通常主要包含变换，量化和熵编码三个阶段。

变换过程将图像从空间像素域映射到变换域，目的是去除像素间的相关性，使数据更容易被编码。

变换编码是一种去除空间冗余的有效编码方式，通过将空间域信号转换成频域信号，来将信号的能量进行重新分布，从而实现信号在变换后的空间也即频域空间的压缩。目前，我们普遍应用的变换编码技术有 K-L(Karhunen-Loeve)变换、离散余弦变换（DCT）和小波变换。离散余弦变换是目前最为成熟同时也是最为接近 K-L  变换的一种技术，已被广泛应用于视频图像压缩领域，例如，H.264、MPEG4、JPEG 等国际视频图像压缩标准中都采用了该技术。DCT 是基于像素块进行变换的，而无法消除其块边界间的相关性，因此会出现我们常说的方块效应。而小波变换是在Fourier 变换的基础上发展起来的，因其良好的多分辨分析及局部变换特性，近年来被致力于视频图像处理领域的研究中。例如在视频图像压缩技术研究中，出现的较为经典的算法有嵌入式小波零树编码算法(EZW)，分层小波树集合分割算法(SPIHT)和集合分裂嵌入块编码算法（EBCOT）都是以小波变换技术为基础的。

量化过程是一个有损的过程，采用不同的量化值对原数据进行分段近似表示，目的是减少每个码字的编码比特数。根据量化间隔是否等分，量化又可以细分为均匀量化和非均匀量化。

所谓量化是一个降低精度，将每个变换后的像素用有限的信号来表示的过程。对于图像上所呈现的信息，人眼根据其视觉特性会具有不同的分辨率，也就是说可以在保证视频图像重构质量的同时，舍弃对人眼视觉效果影响不大的信息。精度的高低取决于量化步长的长短，若量化步长越长，则精度越低，压缩效果较之越好，反之效果越差，该过程要权衡压缩效率及视频重构质量等因素。

熵编码过程主要是通过编码算法将量化后的数据转换成二进制码流，以便更好地存储和传输。解码过程可以看做是编码的逆过程，将二进制码流还原成数据，并根据解成图像重构。

 熵编码是一种基于统计模型的无失真编码压缩技术，通过统计信号出现的概率进行统计从而进行编码，主要用于消除信号间的统计冗余，主要的熵编码技术有游程编码、算术编码和霍夫曼编码，其中以霍夫曼编码最为经典

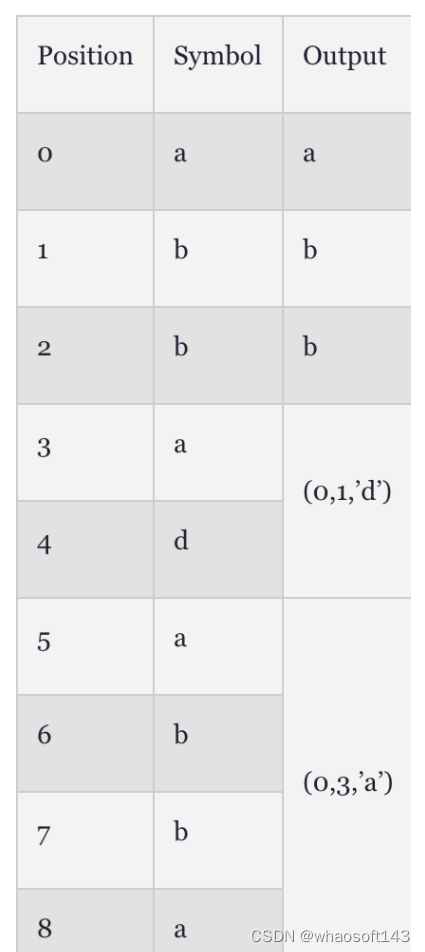
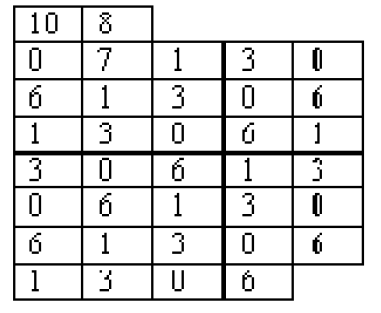
zigzag扫描如上图，行程编码的基本原理是：用一个符号值或串长代替具有相同值的连续符号（连续符号构成了一段连续的“行程”。行程编码因此而得名），使符号长度少于原始数据的长度。 例如：5555557777733322221llllll
行程编码为：（5，6）（7，5）（3，3）（2，4）（l，7）。可见，行程编码的位数远远少于原始字符串的位数。

zig-zag模式图所示。它可以用来按照以下的顺序来提取一个矩阵的元素。

       这个东西用在哪呢？用在离散余弦变换的系数提取里面。离散余弦变换（DCT）是种图像压缩算法，JPEG就是用它来进行图像压缩的。DCT将图像从像素域变换到频率域。然后一般图像都存在很多冗余和相关性的，所以转换到频率域之后，只有很少的一部分频率分量的系数才不为0，大部分系数都为0（或者说接近于0），这样就可以进行高效的编码，以达到压缩的目的。进行离散余弦变换（DCT）得到的系数矩阵图,从左上角依次到右下角，频率越来越高，可以看到，左上角的值比较大，到右下角的值就很小很小了。换句话说，图像的能量几乎都集中在左上角这个地方的低频系数上面了。

       而且，系数的重要性一定d程度上是按照zigzag模式进行排列的。所以就可以通过zigzag模式来提取这个矩阵前面的重要性的元素，作为这个图像在频率域上的特征，然后可以拿去做分类啥的，以达到降维的功效。

最佳截断嵌入码块编码EBCOT

EBCOT编码分为两部分：第1部分tierl，将每个子带划分为独立的编码块，然后对每个编码块独立进行嵌入式编码扫描，每个编码块的比特层编码，最后对编码扫描结果进行MQ算术编码，得到嵌入式码流；第2部分tier2，根据输出码率的要求，组合每个编码块的嵌入式码流，对所有编码块的编码流进行优化截断排序、打包等处理,得到JPEG2000的码流。

参考文献：小波变换在视频图像压缩编码中的应用研究——詹 为 

参考链接：https://blog.csdn.net/ytang_/article/details/76579697
参考链接：https://blog.csdn.net/zouxy09/article/details/13298817