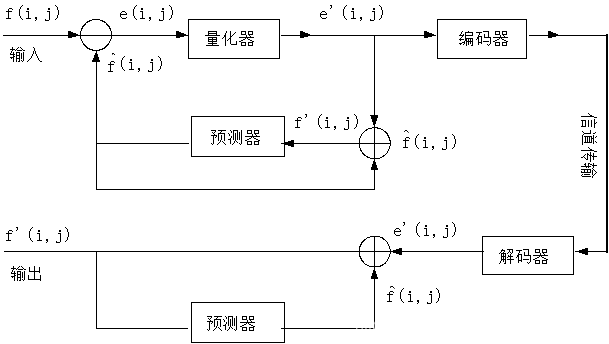
• 信息量过大的情况下使用压缩，如果不压缩系统超载，导致无法发送图片或视频，所以进行压缩处理

（这里的图像压缩指的是有损压缩）
下图是一个像素为$512\times 512$的图像，黑点表示为一个像素
这个像素表示的灰度值[0，255]

我们把一个像素表示为Xi，Xi通常是[0,255]中的一个数，也就是$2^8$种可能，占八个比特位；图像中共有$512\times 512$个像素；
我们实际上就是对$R^n$中的向量x做操作，n=$512\times 512$
一个图像得到一个长度为$R^n$的向量
如果是彩色图像长度为三倍（也就是$3\times 512^2$)，所以需要三个值来表示

• 标准的压缩处理方式是JPEG.
  （实际上就是做基变换）

标准基是每个像素一个值，现在我们有一个长度为$512\times 512$的向量x，如下图向量x
假设第i个位置数值为121，下一个位置数值为124，若121为蓝色，124为与蓝色相接近的颜色，越往后数值越多，不同颜色开始出现，非常接近的像素，使他们相互关联，就有了压缩的可能性
特点：我们得到的大多数像素点，其灰度和相邻像素灰度值一样
我们利用这一特点，知道一组非常好的基向量是全为1的向量
一个向量就能完整的给出所有像素一致图像的信息
当然我们的图像像素不是一致的，混合一些其他信号
但是这样一组基向量也能解决很大问题，你可能会有疑问，那么除了这组向量其他的向量是多少？？

在极端情况下，基中向量如上图所示；像一个巨大的棋盘；

图像的另一种情况：一半暗一半亮
则向量就为一半正一一半负一；

• 基变换

• 傅里叶基{包含常数向量}（图二）
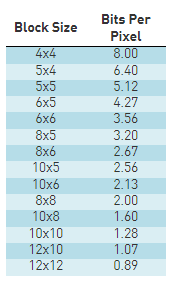
  通常$8\times 8$是个很好的选择，$8\times 8$指的是对于一个大的信号，例如把$512\times 512$分解成$8\times 8$的小块，每一块内有64个系数，64个基向量，64个像素，在64维空间中利用傅里叶向量做基变换

• 这是无损压缩步骤

1.输入信号x
2.进行基变换，选择一组更好的基，得到系数c
例如，输入是64个像素，得到64个系数，然后压缩，（我们知道$R^{64}$有很多组基，我们已经选取了一组，我们用内组基把信号表达出来）
损失究竟干了什么？？

• 我们可以扔掉小的系数，叫做阈值量化，设定我们人眼看不出区别的阈值，不在其中，超过阈值的，丢掉，我们看不出任何区别，压缩步骤后得到压缩后的一套压缩系数（很多为0），用这些系数C重构信号X，（$x=\sum C\times Vi$)Vi为每个系数对应基向量，这个求和有损失，肯定比64项少
  以上是对于图像和信号的压缩。

对于视频呢？？

我们可以把视频想象成一幅幅静态的图像，压缩每一幅，然后播放，做成视频，但这种方法并不可取，视频每一幅图像和下一个很接近，具有相关性，所以我们要用预估和修正，两张图象非常接近，我们假设他们是同一幅，然后加一个小小的修正，而我们只需对修正数字和编码化，然后对修正量进行压缩

实际上在时间和空间上事物不会瞬间改变，通常是很平滑的变化，可以根据前一个值预测一个值出来

关于线性代数问题，就是找出系数，假设给定基，和像素值

• 一组新基，我们叫做小波
  我们用$8\times 8$的情况来描述这组基
  小波基：
  小波基是一组正交基
• 如果列向量标准正交，那么逆等于其转置

最快的是保持八个像素不变，八个基向量不变，但是对于压缩的角度来看，若从十压缩到一，扔掉了90%的像素，图像变黑，但相反如果基的性质好，像傅里叶基和小波基，扔掉c5,c6,c7,c8,扔掉的只是很少的点，
一组好基的性质：

• 计算快
• 少量基向量就能接近信号，良好的压缩性（少量基向量就能够重现图像）

基变换

• 已知一个基上的向量变换到不同的基中
• 

已知线性变换T对于$n\times n$的矩阵来说，对于给定基进行计算（变换T已经给定，旋转，投影等）
加下来创建矩阵：
创建矩阵A，基为V1-V8
以同样的方式创建矩阵B，基为W1-W8
因为A，B来自同一变换，所以A和B之间有一定的关系，因为是同一个变换，在一组基上计算得到一个矩阵，然后再另一组基上计算，得到的两个矩阵是相似的

• 两个矩阵相似，B=M逆AM，M就是基变换矩阵
  
  知道T作用在每个基向量的结果，就知道了一切
  如果给定一个变换和一组基，给定的是这些基，告诉你变换，然后来计算T作用在每个基上，将结果展示成基的形式，就得到64个数

• 假设V1-V8这组基是特征向量，则T(v)=v的倍数，二者同向，那么A是多少？？

• 其实最好的基是特征向量基，但是寻找特征基向量的代价大，所以选用寻找代价小的基且接近的基，例如小波基