专栏导读
- 作者简介:工学博士,高级工程师,专注于工业软件算法研究
- 本文已收录于专栏:《复杂函数拟合案例分享》本专栏旨在提供 1.以案例的形式讲解各类复杂函数拟合的程序实现方法,并提供所有案例完整源码;2.复杂函数包含:分段函数、积分函数、常/偏微分函数、隐函数、方程组、级数函数、多参数函数;3.拟合工具是Matlab种的lsqcurvefit, nlinfit,神经网络,ga遗传算法,MultiStart全局优化算法等;4.拟合案例均源自科研实践中遇到的案例,文本教程+视频教程+案例源码,三向强化学习!提高大家解决实际数学建模的问题。
- 【案例源码地址】
- 【视频课程地址】https://www.bilibili.com/video/BV1bQ4y1U7mu/?spm_id_from=333.337.search-card.all.click
- 欢迎订阅专栏,订阅用户可私聊进入Matlab编程交流群(知识交流、问题解答),并获赠丰厚的Matlab相关学习资料(教材、源码、视频课)
- 专栏订阅地址:https://blog.csdn.net/u010542847/category_12576325.html
【总体简介】💻🔍
你将获得: 分段微分方程组拟合案例【matlab源码】+视频程(试看)
获取连接:Matlab分段微分方程组拟合【案例源码】
本案例通过Matlab中的lsqcurvefit()实现分段微分方程组的拟合,案例有三个难点:1.自定义拟合函数通过微分方程(求解)表示;2.微分方程分段;3.微分方程本身是方程组的形式。具体方程形式如下图所示。
需要说明的是由于待拟合参数过多,所以由于lsqcurvefit()拟合工具自身局限性,最终本案例拟合的精度并不高,但是本拟合案例的主要目的是提供一种方法,当待拟合参数较少时,会有一个理想的结果。程序可以成功运行进行迭代拟合,并得到拟合结果。拟合精度不够高的原因主要在于方程过于复杂,待拟合参数过多,超出lsqcurvefit本身适合的参数个数,如果参数个数<=5,是可以得到较好的拟合结果。

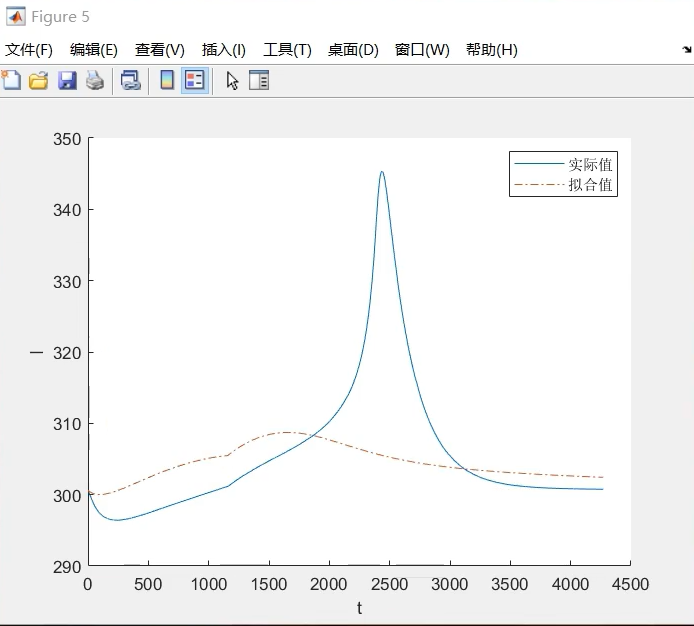
【拟合结果】
拟合精度不够高的原因主要在于方程过于复杂,待拟合参数过多,超出lsqcurvefit本身适合的参数个数,如果参数个数<=5,是可以得到较好的拟合结果。
【视频教程】
本案例已收录至b站的《Matlab复杂函数非线性拟合》专题课程【Matlab复杂函数非线性拟合专题/lsqcurvefit/nlinfit/积分函数、微分函数、隐函数、方程组、最小二乘法/机器学习/神经网络/编程/人工智能】 Matlab复杂函数非线性拟合专题/lsqcurvefit/nlinfit/积分函数、微分函数、隐函数、方程组、最小二乘法/机器学习/神经网络/编程/人工智能_哔哩哔哩_bilibili