蓝桥集训之糖果

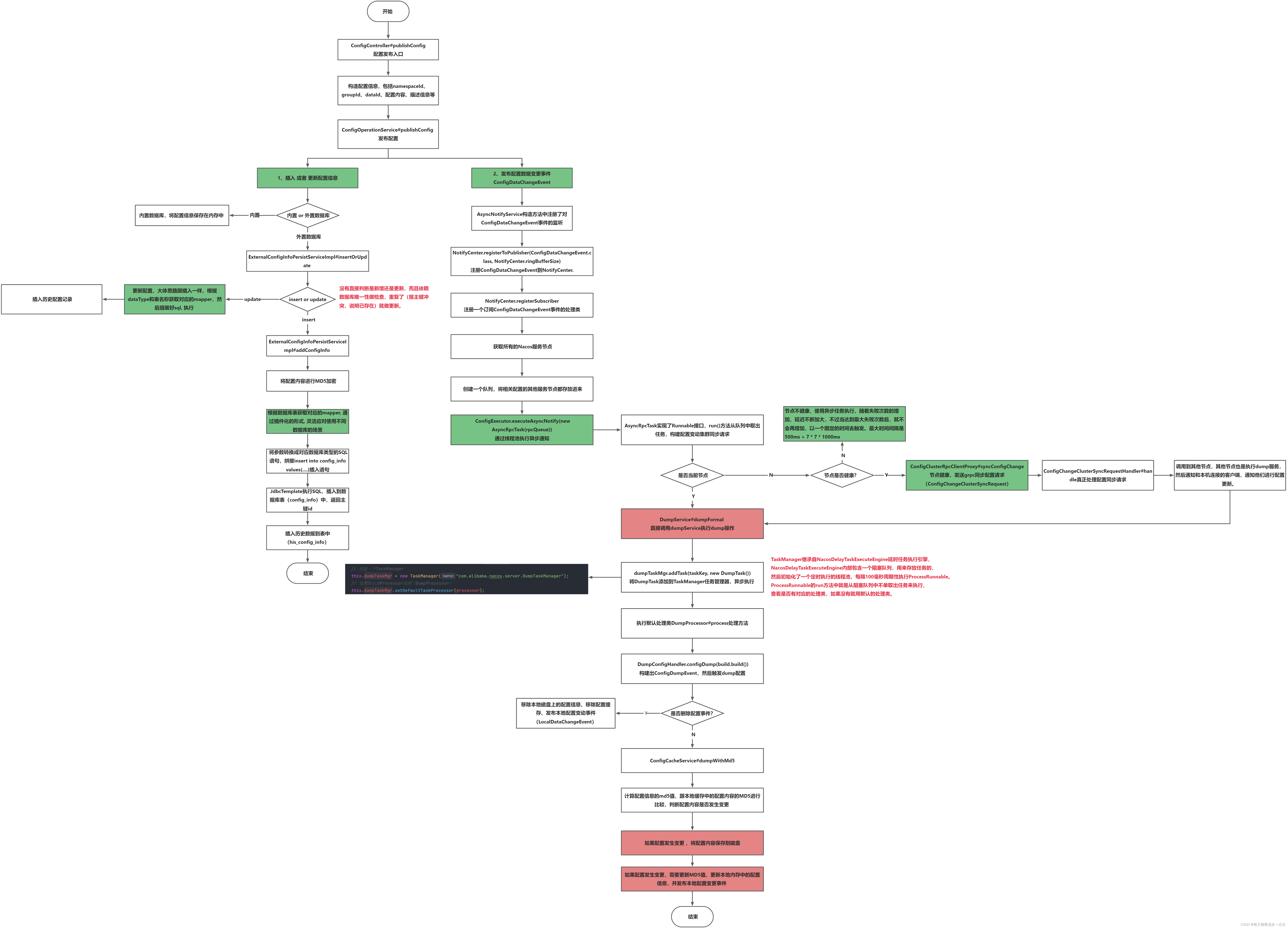
核心思想：dfs + 剪枝 + 重复覆盖问题
- 暴搜直到所有列都覆盖
- 优化：
  - 1.迭代加深答案从1开始++
  - 2.逻辑简化每次从可选行数最少得一列开始
  - 3.可行性剪枝添加估值函数h(),表示至少还需要选几行与剩余行数的大小比较
  - 4.**位运算 **将每包糖果以二进制数存下有口味为1 没有口味为0

  #include <iostream>#include <cstring>#include <algorithm>#include <vector>using namespace std;const int N = 110 , M = 1<<20; int n,m,k;//找第几位是1 例如log2[100] = 2,log2[1000] = 3int log2[M];vector<int> col[N];  //放每种口味糖果可以用哪几张图int lowbit(int x){return x & -x;}int h(int state)  //至少还要选几包{int res=0;for(int i=(1<<m)-1-state;i;i-=lowbit(i)){int c = log2[lowbit(i)];res ++;//见优化3for(auto row:col[c])  i &= ~row;}return res;}bool dfs(int depth,int state){if(!depth || h(state) > depth) return state == (1<<m) -1;int t = -1;//从当前图开始遍历 找最少可选行最少的for(int i=(1<<m) -1 - state;i;i-=lowbit(i)){int c = log2[lowbit(i)];if(t == -1 || col[c].size() < col[t].size()) t = c;}//遍历该行for(auto row:col[t]){//或运算 看看行不行if(dfs(depth-1,state|row)) return true;}return false;}int main(){cin>>n>>m>>k; for(int i=0;i<m;i++) log2[1<<i] = i;  //预处理log2for(int i=0;i<n;i++){int state = 0;for(int j=0;j<k;j++){int c;cin>>c;state |= 1<<(c-1);  //把这张图补充到state上  或运算}for(int j=0;j<m;j++)  //遍历每一种口味if(state>>j & 1)  //如果有这种口味col[j].push_back(state);}//去重 每一种口味的方案都要去for (int i = 0; i < m; i ++ ){sort(col[i].begin(), col[i].end());col[i].erase(unique(col[i].begin(), col[i].end()), col[i].end());}int depth = 1;while(depth <= m && dfs(depth,0) == 0)  //从1开始找答案{depth ++;}if(depth>m) depth = -1;cout<<depth<<endl;}