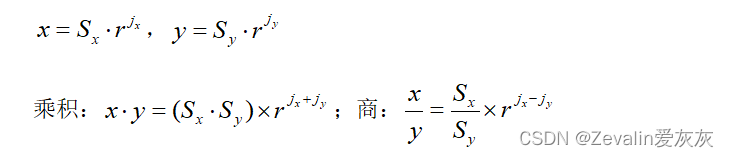写在前面:
- 本系列笔记主要以《计算机组成原理(唐朔飞)》为参考,大部分内容出于此书,笔者的工作主要是挑其重点展示,另外配合下方视频链接的教程展开思路,在笔记中一些比较难懂的地方加以自己的一点点理解(重点基本都会有标注,没有任何标注的难懂文字应该是笔者因为强迫症而加进来的,可选择性地忽略)。
-
视频链接:计算机组成原理(哈工大刘宏伟)135讲(全)高清_哔哩哔哩_bilibili
一、浮点加减运算
1、浮点加减运算的步骤
(1)对阶,使两数的小数点对齐。
(2)尾数求和,将对阶后的两尾数按定点加减运算规则求和(差)。
(3)规格化。(这一步是为了增加有效数字的位数,提高运算精度)
(4)舍入,要考虑尾数右移时丢失的数值位。
(5)溢出判断,即判断结果是否溢出。
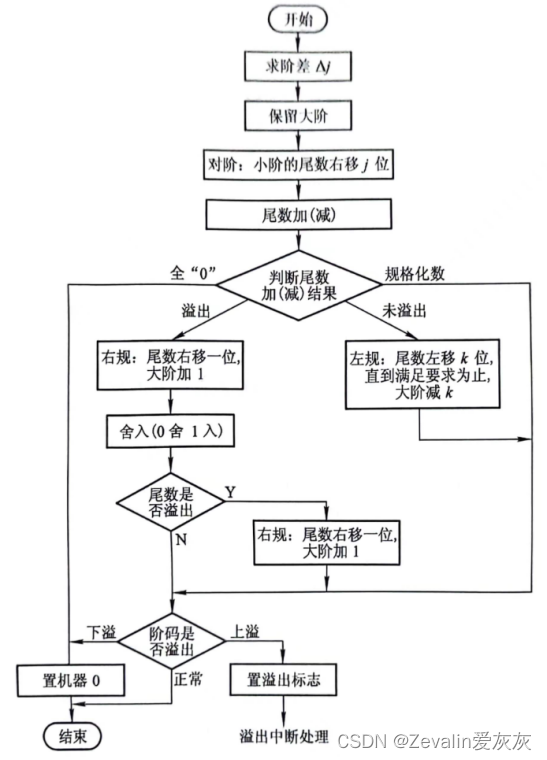
2、对阶
对阶的目的是使两操作数的小数点位置对齐,即使两数的阶码相等。为此,首先要求出阶差,再按小阶向大阶看齐的原则,使阶小的尾数向右移位,每右移一位,阶码加1(这是基值为2的情况,下面都以基值为2进行介绍),直到两数的阶码相等为止,右移的次数正好等于阶差(尾数右移时可能会发生数码丢失,影响精度)。
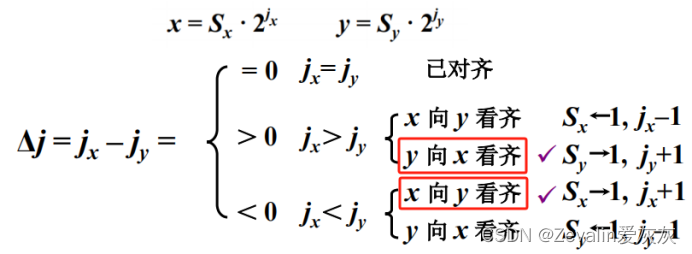
3、尾数求和
将对阶后的两个尾数按定点数加(减)运算规则进行运算。

4、规格化
(1)当基值r=2时,尾数S的规格化形式为。
(2)尾数是否符合规格化形式的判断方式如下:(图中没展示符号位)

(3)当一个数不满足规格化形式式,需要对其进行规格化。
①当尾数出现“00.0××…×”或“11.1××…×时”,需左规,左规时尾数左移一位,阶码减 1,以此往复,直到数符和第一数位不同为止。
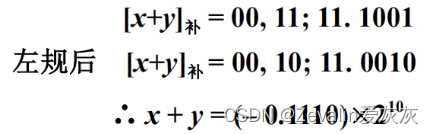
②当尾数出现“01.××…×”或“10.××…×时”(尾数溢出),需右规,右规时尾数右移一位,阶码加1。
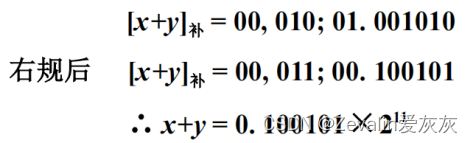
5、舍入
(1)在对阶和右规的过程中,可能会将尾数的低位丢失,从而引起误差,影响精度,为此可用舍入法来提高尾数的精度。
(2)常用的舍入方法有以下两种:
①“0舍1入”法:在尾数右移时,被移去的最高数值位为1则在尾数的末位加1(这样做可能使尾数又溢出,此时需再做一次右规),被移去的最高数值位为0则舍去。
②“恒置1”法:尾数右移时,不论丢掉的最高数值位是“1”或“0”,都使右移后的尾数末位恒置“1”(这种方法同样有使尾数变大和变小两种可能)。
6、溢出判断
(1)设机器数为补码,尾数为规格化形式,并假设阶符取2位,阶码的数值部分取7位,数符取2位,尾数取n位,则该补码在数轴上的表示范围如下。
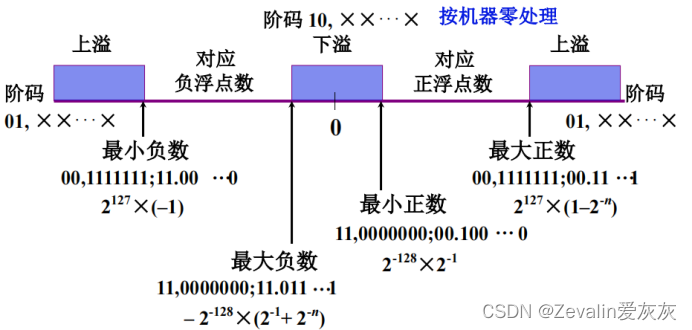
(2)浮点机的溢出与否可由阶码的符号决定,即:

二、浮点乘除法运算
1、浮点乘除法运算过程
(1)两个浮点数相乘,乘积的阶码应为相乘两数的阶码之和,乘积的尾数应为相乘两数的尾数之积。
(2)两个浮点数相除,商的阶码为被除数的阶码减去除数的阶码,尾数为被除数的尾数除以除数的尾数所得的商。
2、阶码运算
(1)做乘法运算时,需要阶码求和:
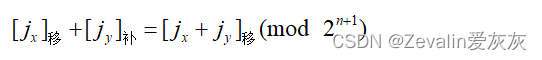
(2)做除法运算时,需要阶码相减:
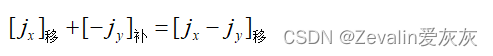
(3)阶码采用移码表示后,如果在原有移码符号位的前面(即高位)再增加1位符号位,并规定该位恒用“0”表示,便能方便地进行溢出判断。
①溢出的条件是运算结果移码的最高符号位为1,此时若低位符号位为0即表示上溢,低位符号位为1即表示下溢。
②如果运算结果移码的最高符号位为0,即表明没有溢出,此时若低位符号位为1即表明结果为正,低位符号位为0即表示结果为负。
3、尾数运算
(1)浮点乘法尾数运算:
①检测两个尾数中是否有一个为0,若有一个为0,乘积必为0,不再做其它操作;如果两尾数均不为0,则可进行乘法运算。
②两个浮点数的尾数相乘可以采用定点小数的任何一种乘法运算来完成。相乘结果可能要进行左规,左规时调整阶码后如果发生阶下溢,则作机器零处理;如果发生阶上溢,则作溢出处理。此外,尾数相乘会得到一个双倍字长的结果,若限定只取1倍字长,则乘积的若千低位将会丢失,如何处理丢失的各位值,通常有两种方法。
[1]其一,无条件地丢掉正常尾数最低位之后的全部数值,这种方法称为截断处理,处理简单,但影响精度。
[2]其二,按浮点加减运算讨论的两种舍入原则进行舍入处理。对于原码,采用0舍1入法时不论其值是正数或负数,“舍”使数的绝对值变小,“入”使数的绝对值变大。对于补码,采用0舍1入法时,若丢失的位不是全0,对正数来说,“舍”“入”的结果与原码分析正好相同;对负数来说,“舍”“入”的结果与原码分析正好相反,即“舍”使绝对值变大,“入”使绝对值变小。为了使原码、补码舍入处理后的结果相同,对负数的补码可采用如下规则进行舍入处理。
#1 当丢失的各位均为0时,不必舍入。
#2 当丢失的各位数中的最高位为0时,且以下各位不全为0,或丢失的各位数中的最高位为1,且以下各位均为0时,则舍去被丢失的各位。
#3 当丢失的各位数中的最高位为1,且以下各位又不全为0时,则在保留尾数的最未位加1修正。
(2)浮点除法尾数运算:
①检测被除数是否为0,若为0则商为0;再检测除数是否为0,若为0则商为无穷大,另做处理。若两数均不为0,则可进行除法运算。
②两浮点数尾数相除同样可采取定点小数的任何一种除法运算来完成。对已规格化的尾数,为了防止除法结果溢出,可先比较被除数和除数的绝对值,如果被除数的绝对值大于除数的绝对值,则先将被除数右移一位,其阶码加1,再作尾数相除,此时所得结果必然是规格化的定点小数。
三、浮点运算所需的硬件配置
由于浮点运算分阶码和尾数两部分,因此浮点运算器的硬件配置比定点运算器的复杂。分析浮点四则运算发现,对于阶码只有加减运算,对于尾数则有加、减、乘、除四种运算。可见浮点运算器主要由两个定点运算部件组成,一个是阶码运算部件,用来完成阶码加、减,以及控制对阶时小阶的尾数右移次数和规格化时对阶码的调整;另一个是尾数运算部件,用来完成尾数的四则运算以及判断尾数是否已规格化;此外,还需有判断运算结果是否溢出的电路等。
现代计算机可把浮点运算部件做成独立的选件,或称协处理器,用户可根据需要选择,不用选件的机器,也可用编程的方法来完成浮点运算,不过这将会影响机器的运算速度。