背景介绍
子图计数(Subgraph Counting)是图分析中重要的研究课题。给定一个查询图 和数据图 , 子图计数需要计算 在 中子图匹配的(近似)数目 。一般我们取子图匹配为子图同构语义,即从查询图顶点集 到数据图顶点集 的单射 ,保持拓扑关系(当查询图存在边 时,数据图中对应点也需要有连边 )和标签(查询图顶点 和数据图中对应点 标签相同)不变。
子图计数可以用于需要(近似)子图匹配数目的场景,如,图数据库查询优化时,需要对特定查询结构做基数估计(cardinality estimation),这便可以应用子图计数方法。
一般方法
最直接的方法是直接在数据图上运行查询图的子图匹配算法。优点是可以得到精确的子图计数结果。但子图匹配是 NP 难问题,真实运行子图匹配算法可能需要很长时间,且有时用户并不需要得到精确结果。于是研究者们提出了基于摘要的和基于采样的两大类子图计数方法[^1]。
基于摘要的(summary-based)的子图计数方法通过预处理数据图,统计一些元数据(例如一些子结构的真实计数数目)并储存起来。每当遇到一张新查询图需要估计其计数时,将其分解成若干部分,每一部分都可以用存储的统计信息容易估计计数。再用独立性假设(假设各子结构之间是相互独立的)或其他连接估计的方法合成原查询图的计数估计。代表方法有 CharacteristicSets,SumRDF 等。
基于采样的(sampling-based)的子图计数方法在数据图的采样上匹配查询图,再根据采样的比例还原出原数据图上的计数估计。其能消除一部分基于摘要方法的独立性假设带来的误差。但由于采样的随机性,如果样本集过小,估计偏差会很大;如果样本集过大,估计代价也会很大。代表方法有 IMPR,Wander Join等。
近年来深度学习,尤其是图神经网络(graph neural network, GNN)的兴起给子图计数的研究带来了新思路。直观上,如果神经网络能够很好地表示和编码查询图和数据图的拓扑结构和标签信息,那只需要训练一个求解回归问题的黑盒模型,输入查询图的表示 和数据图的表示 ,输出子图计数的估计值 便可完成该任务(训练误差一般取 ,其中 ,越接近 表示估计得越准)。于是涌现了很多方法,致力于改进查询图和数据图的编码表示,改进估计模型,以及顶层设计。本文接下来会介绍三篇具有代表性的工作。
方法介绍
NSIC
NSIC[^2]是最早将 GNN 应用于子图计数问题的工作。其提出了一个端到端的预测框架,框架内的几个模块可以选用适合不同数据集的方法。其思想较为朴素,架构如下图所示,符合上一部分的介绍。

对于查询图和数据图的表示,NSIC 提出两套解决方案:一是类似语言问题的序列模型(下图中间),将图表示为图中所有边的序列,可以采用 CNN,LSTM,TXL 等方法;二是采用图编码方式(下图右边),在查询图和数据图上运行图神经网络获得各节点的表示,可以采用 RGCN,GIN 等方法。

有了查询图和数据图的表示 和 ,NSIC 提出了一种交互 和 的网络 DIAMNet,在每一步过程中,历史信息先与查询图表示作用,再接受数据图的交互形成新的历史信息。网络最后的输出便能学习到查询图和数据图的特征用于最后的子图计数预测。
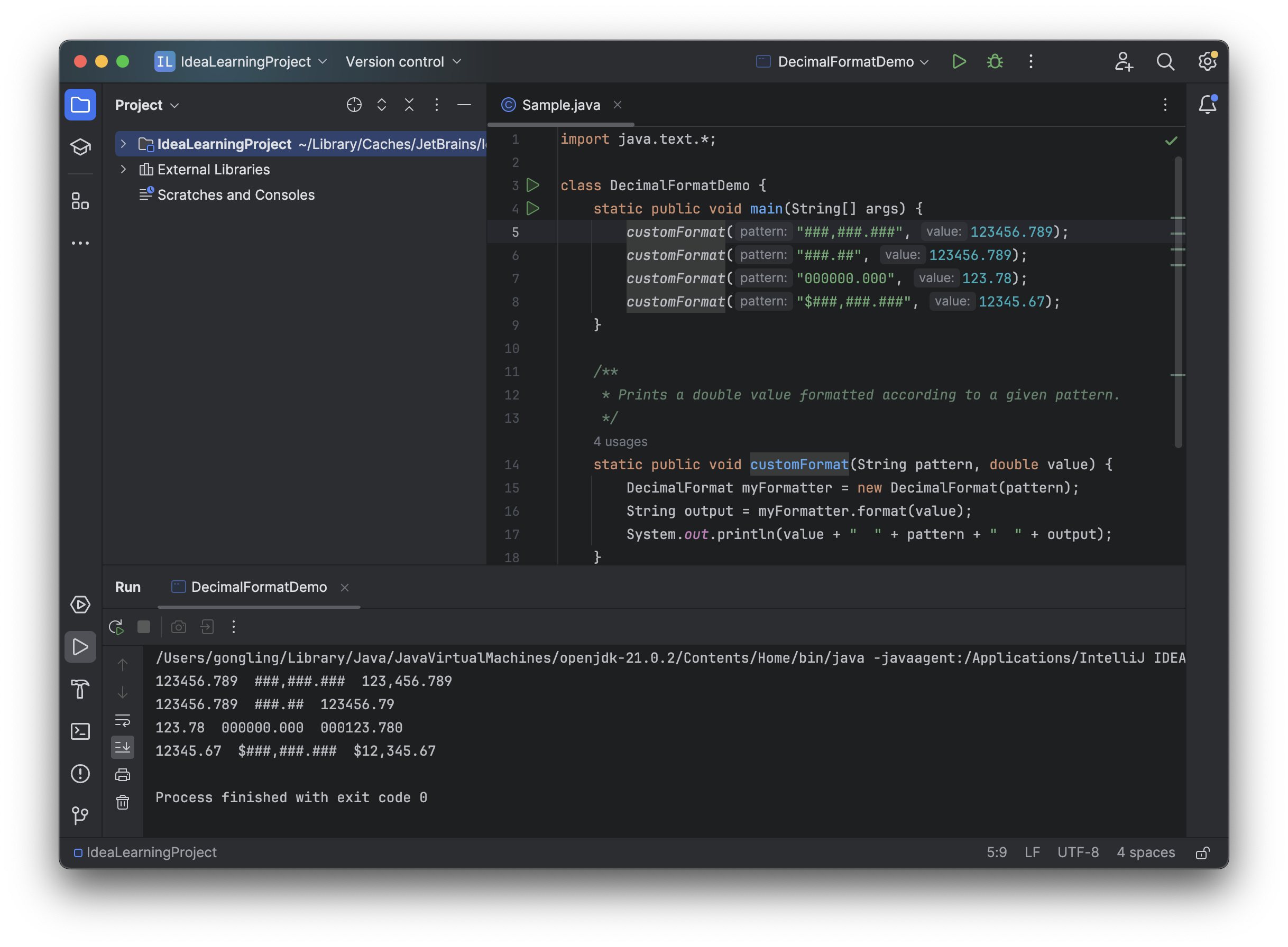
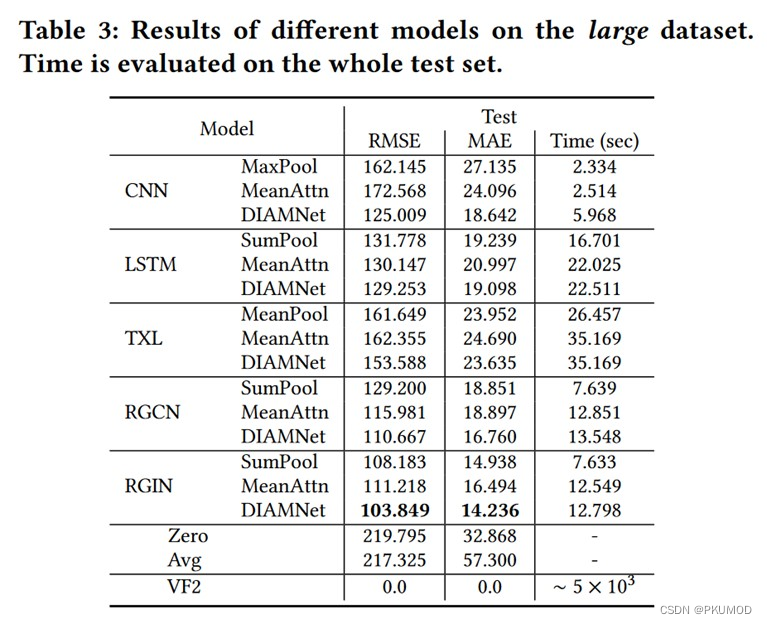
原文实验部分对比了 NSIC 的预测准确度和与基准方法 VF2 (VF2是经典的子图匹配算法,可以得到精确的子图计数结果)的运行时间比较。可以发现,编码查询图和数据图模块上,图编码方法(RGCN, RGIN)比序列编码方法(CNN,LSTM,TXL)更准确。并且在可接受误差范围内,NSIC 比子图匹配方法 VF2 快两到三个数量级。
ALSS
由于 NSIC 需要在原数据图上运行深度模型,代价较大。事实上,NSIC 论文实验中并没有与传统子图计数方法比较,其在运行时间上,并不占优。2021 SIGMOD 的一篇工作 ALSS[^3]并不直接在数据图上运行深度模型,而是直接用查询图的表示作为深度模型的输入,输出子图计数的估计,可以极大提高运行时速度。

其架构如上图所示。为了避免在数据图上做 GNN,需要有查询图更准确的编码。 ALSS 采用传统子图计数的思想,将查询图分解成若干子部分,再将不同部分聚合。具体做法为,从查询图的每个点 出发,做 层 BFS,得到子结构 ,之后在每个 上运行 GNN,取 中 的编码 作为查询图中节点 的编码。后续的子图计数预测的输入就仅为查询图的表示 。数据图的作用仅为查询图上获得每点编码时为每点赋特征初值。文中推荐用频率编码(即每个标签有其 one-hot 向量,编码了数据图中含有该标签点的数目)和嵌入编码(offline地在增强图(原数据图中增加标签点,并连接每个数据点和对应标签构成一个新的图)上运行 GNN,获得标签节点的表示作为含该标签的点的表示,具体如下图)的黏合作为查询图节点的初始特征。

此外 ALSS 还有主动学习模块。在预测计数的回归模型之外,还额外配备了预测计数量级的分类器。当模型训练好之后,遇到一个新的待预测的数据,若分类器结果和回归预测值相差较大,可以认为模型对这条输入数据的预测把握不大,于是将其加入训练集,并请求数据库计算匹配获得其准确计数,每隔一段时间后便重新训练,整体流程如下:

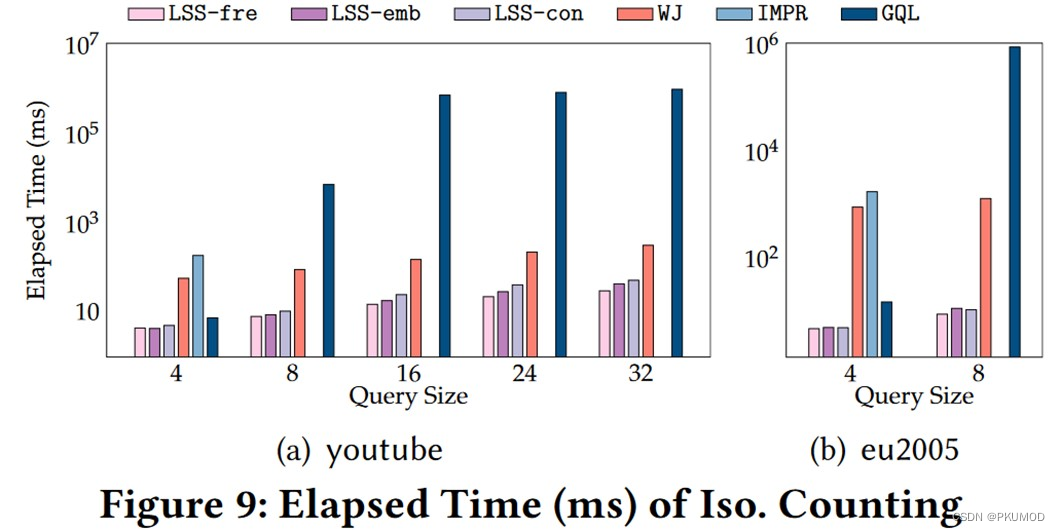
作者在实验中展示了 ALSS 的预测准确性和运行时间。在准确性方面(下图展示了在 aids 数据集上的性能),ALSS (LSS-fre,LSS-emb,LSS-con)尽管没有基于采样的 Wander Join (WJ)方法在小规模查询图表现好,但对于大规模查询图稳定性好。在运行速度方面(下面第二张图展示了在 youtube 和 eu2005 数据集上的运行速度),由于 ALSS 只需要在查询图上运行深度模型,速度比基于采样的 WJ 快很多。

NeurSC
我们可以发现,NSIC 对数据图操作量太大导致其速度慢;而 ALSS 中数据图仅用于查询图表示赋初值,对数据图利用较少。有没有对数据图适中利用的思路呢?NeurSC[^4]是 SIGMOD 2022 的一篇工作。就提出了一种解决思路。
子图匹配方法通常遵循“过滤(filter)- 计划(plan)- 枚举(enumeration)”的框架:过滤阶段通过简单的查询图限制筛选出数据图中有希望构成匹配的相关数据点,计划节点产生一个较优的节点枚举顺序,最后进行枚举。其中,过滤阶段用时很少,占比最多的是枚举阶段。
NeurSC 将子图匹配的过滤操作引入子图计数问题。易见,如果用过滤后的部分数据图代替原数据图,不仅规模变小便于计算,而且剩余的数据图部分也比被过滤的部分对匹配结果的相关性更高。下图是 NeurSC 的架构展示。其中包括了两个 GNN:图内神经网络 (Intra-GNN)运行在查询图和过滤后的数据图上,分别得到其表示;图间神经网络(Inter-GNN)运行在数据图和查询图的交互图上。如下面右图所示,交互图连接了查询图中的点和过滤后数据图对应的候选点。最后将这两部分 GNN 输出的编码输入到预测计数的 MLP 便可得到子图计数的估计。
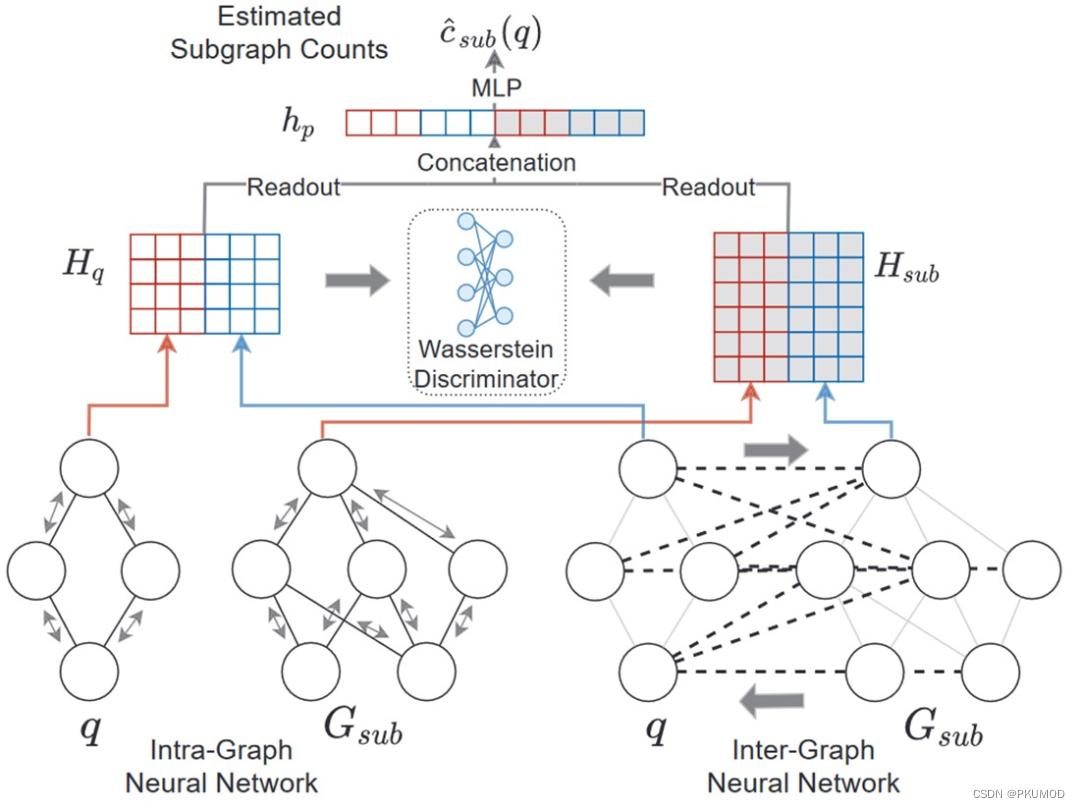
与此同时,为了让查询图中点的表示和过滤后数据图上对应候选点的表示尽可能相同,作者提出了利用 Wasserstein 判别器帮助图内神经网络和图间神经网络对查询点和对应候选点学出相近表示的方法。感兴趣的同学可以阅读原文了解更多。
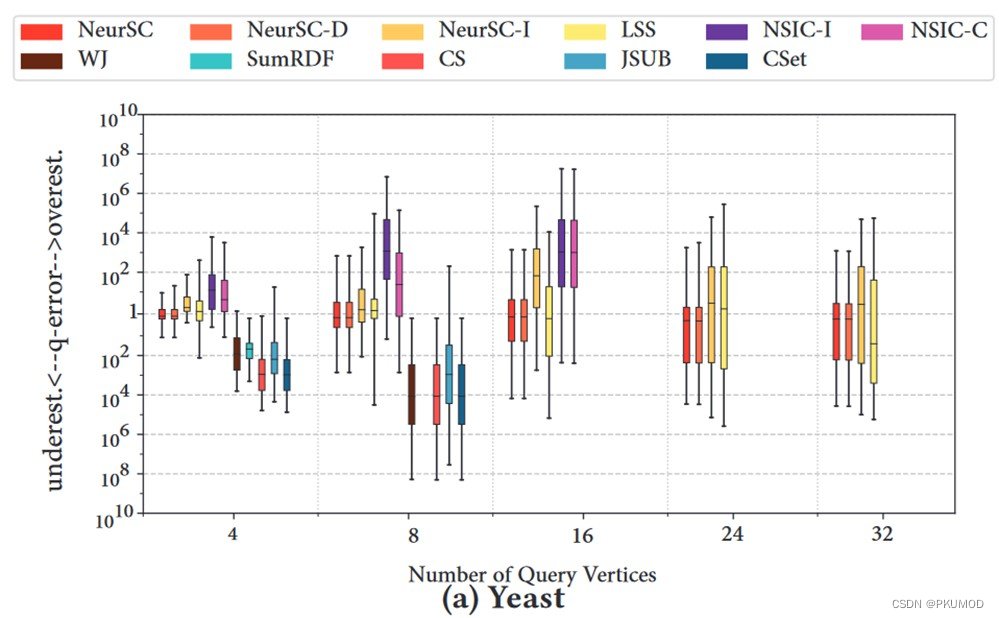
实验部分中对比了 NeurSC 和其他方法的准确性和运行速度,可以发现,NeurSC 有很好的预测精度和稳定性特别是在小规模查询图上。NeurSC 由于引入了过滤后的数据图,而过滤效果不好时,数据规模和原图是差不多大的,速度方面会受到一定影响。
参考文献
[1]: G-CARE: A framework for performance benchmarking of cardinality estimation techniques for subgraph matching. Yeonsu Park, Seongyun Ko, Sourav S. Bhowmick, Kyoungmin Kim, Kijae Hong, and Wook-Shin Han. SIGMOD 2020.
[2]: Neural Subgraph Isomorphism Counting. Xin Liu, Haojie Pan, Mutian He, Yangqiu Song, Xin Jiang, and Lifeng Shang. KDD 2020.
[3]: A Learned Sketch for Subgraph Counting. Kangfei Zhao, Jeffrey Xu Yu, Hao Zhang, Qiyan Li, and Yu Rong. SIGMOD 2021.
[4]: Neural Subgraph Counting with Wasserstein Estimator. Hanchen Wang, Rong Hu, Ying Zhang, Lu Qin, Wei Wang, and Wenjie Zhang. SIGMOD 2022.





![Python算法题集_实现 Trie [前缀树]](https://img-blog.csdnimg.cn/direct/5a897d6e99aa4f639286febc56714d68.png#pic_left)