文章目录
- 前言
- 梯度概述
- 梯度下降算法
- 梯度下降的过程
- optimize优化器
- 梯度问题
- 梯度消失
- 梯度爆炸
- 损失函数
- 常用的损失函数
- 损失函数使用原则
- 激活函数
- 激活函数和损失函数的区别
- 激活函数Relu-隐藏层
- 激活函数Sigmoid和Tanh-隐藏层
- Sigmoid函数
- Tanh(双曲正切)
- <br />softmax激活函数-输出层
- 总结
前言
自定义神经网络一之Tensor和神经网络
自定义神经网络二之模型训练推理
我们在模型篇介绍了模型的基础概念以及训练和推理的过程。在模型训练部分有提到几个概念,例如:
- 参数更新:利用优化算法(如梯度下降算法)根据梯度信息对模型参数进行更新。
- 损失函数: 将模型预测的结果与真实标签进行比较,计算模型的误差。
- 激活函数: 每个神经元接收到输入后对其加权求和,然后传递给激活函数,根据激活函数的结果确定神经元的输出。
那么梯度是什么意思呢?梯度下降又是什么意思?常见的梯度问题有哪些? 损失函数是什么意思?损失函数和激活函数的区别是什么呢?
梯度概述
梯度的方向是函数在某一点变化最快的方向。也就是说,如果你站在一座山上,梯度的方向是指向山坡最陡峭(上升最快)的方向。如果你需要找到函数的最大值,那你应该朝着梯度的方向前进,因为这样能使函数值最快地上升。
梯度下降算法
神经网络的两种数字运算。前向传播是指预测给定输入向量的输出的计算过程,而反向传播和梯度下降描述的是改进网络的权重和偏差以做出更好预测的过程。
梯度下降是一种常用的优化算法,其目标是找到某个函数的最小值。在机器学习和深度学习中,这个函数通常是损失函数,即模型预测的输出值和实际值之间的差异度量。
在深度学习中,我们通常希望找到损失函数的最小值,也就是我们希望找到山谷而不是山顶。因此,我们需要朝着梯度的反方向,也就是下山的方向前进。这就是为什么这种方法叫做"梯度下降",我们是在"下降",向着梯度的反方向移动。
对于机器学习或深度学习模型,参数就是你的位置,损失函数就如同山的高度。你希望找到能使损失最小的参数。具体地,你会计算损失函数对每个参数的梯度,然后将参数向梯度的反方向更新一小步。这个步长,也叫做学习率,是需要手动设置的。
通过重复这个过程多次,参数将会接近到使损失函数值最小的位置。这就是为什么梯度下降可以被用来最小化模型预测的输出值和实际值之间的差异,也就是损失函数的值。
梯度下降的过程
具体的操作过程是这样的:
第一步,先前向传播:首先,网络会进行前向传播操作,从输入层开始,依次通过每一层,最后到达输出层并生成预测值。在这个过程中,每一层的输入都是上一层的输出。
第二步,计算损失:当网络生成了预测值后,就可以计算出预测值与真实值之间的差异,也就是损失函数的值。
第三步,反向传播误差:这是反向传播的关键步骤。开始于输出层,计算损失函数对每一层的参数(权重和偏置)的梯度。这一步通常通过链式法则完成。
第四步,更新参数:一旦计算出了每个参数的梯度,就可以使用这些梯度来更新参数。更新的方式通常是:新的参数值 = 原来的参数值 - 学习率 * 梯度。这个过程就是梯度下降的过程。
这个过程会反复进行,每进行一次,网络的预测值就会更接近真实值,损失函数的值就会更小。直到达到设定的迭代次数,或者损失函数的值已经足够小,训练过程就会结束。
optimize优化器
神经网络的目标是找到一组权重参数,可以使损失函数的值最小。这就是一个优化问题,在这个问题中,损失函数就是我们需要最小化的目标函数。
然而,手动寻找这样一组参数是很困难的,因为参数的数量通常非常大,且权重参数与损失函数之间的关系非常复杂。因此,我们需要借助优化器自动进行这一过程。
优化器的工作原理是,首先,计算损失函数相对于每个参数的梯度,也就是每个参数变动一点点,损失函数会变化多少。然后,根据这个梯度,进行一次优化步骤,也就是更新参数的值。具体的更新策略会由所选择的优化器决定。
例如,SGD(随机梯度下降)优化器会直接减去学习率乘以梯度的结果来更新参数。这样,如果损失函数对某个参数的梯度为正,那么参数的值就会减小,使得损失函数值降低。反之,如果梯度为负,那么参数的值就会增大。
有很多种优化器,比如SGD、Adam、RMSprop等等,它们都有自己的特点和不同的更新策略。选择哪一种优化器,会依情况而定,它依赖于具体的问题和数据。
通过迭代更新,优化器能够帮助我们找到损失函数最小的权重参数,使得神经网络的预测结果尽可能接近真实值,从而完成神经网络的训练过程。
梯度问题
梯度消失
在神经网络的训练过程中,更新权重依赖于误差反向传播的梯度。然而,某些情况下,梯度可能会变得非常小,以至于权重几乎不会有太大的变化,这就是所谓的‘梯度消失’。这个问题常常出现在深度神经网络中,特别是在使用sigmoid或者tanh等激活函数的情况下,因为这些函数的梯度在接近0或1时会非常接近于0。
解决梯度消失问题的策略:
- 更改激活函数:使用ReLU(Rectified Linear Unit)及其变体(例如Leaky ReLU,PReLU),它们在正值上没有梯度限制,可以缓解梯度消失的问题。
- 使用批量归一化(Batch Normalization):这种技术可以调整每一层的输出,使其保持适当的分布,可以一定程度上防止梯度消失。
- 使用LSTM或GRU等门控循环单元:对于循环神经网络,可以使用LSTM或GRU等门控循环单元,它们设计了专门的机制来捕捉长期依赖,对抗梯度消失的问题。
梯度爆炸
梯度爆炸是指在反向传播过程中,梯度变得非常大,以至于更新的权重过大,导致网络难以收敛。这种现象常见于深度网络和递归神经网络(RNN)。
解决梯度爆炸问题的策略:
- 梯度裁剪(Gradient Clipping):这是一种常见的处理梯度爆炸的策略。当梯度超过某个阈值时,会将其限制在该阈值之内。
- 权重初始化方法:适当的权重初始化方法可以防止梯度在反向传播过程中变得过大或过小。
- 使用批量归一化(Batch Normalization):正如上面所述,它也可以帮助缓解梯度爆炸的问题。
- 使用更小的学习率:如果梯度爆炸导致训练不稳定,可能需要减小学习率。
损失函数
损失函数(Loss Function)是用于度量机器学习模型预测的结果和真实值之间差距的函数。训练机器学习模型的过程,就是让损失函数尽可能小的过程。损失函数的选择会直接影响到模型训练的效果。
常用的损失函数
-
均方误差(Mean Squared Error,MSE):它是最常见的回归损失函数,计算方法为预测值与真实值之差的平方和的均值。MSE对于大的误差值具有很高的惩罚程度,因为差值会被平方。
- MSE(均方误差): 预测值与实际值之差平方的期望值。取值越小,模型准确度越高。
- RMSE(均方根误差):为MSE的平方根,取值越小,模型准确度越高。
- MAE(平均绝对误差): 绝对误差的平均值,能反映预测值误差的实际情况。取值越小,模型准确度越高
- MAPE(平均绝对百分比误差): 是 MAE 的变形,它是一个百分比值。取值越小,模型准确度越高。
-
交叉熵损失(Cross-Entropy Loss):这是处理分类问题最常用的损失函数。在二分类问题中,它的形式与logistic回归的损失函数相同。对于多分类问题,它经常配合Softmax函数使用。
-
Hinge损失(Hinge Loss):这是支持向量机(SVM)中使用的损失函数。如果样本被完全正确分类,且预测结果落在“边界”内,则损失为0;否则,损失为样本到“边界”的距离。
-
Huber损失(Huber Loss):它是均方误差和绝对值误差的折中产物。对于较小的误差,它的行为类似于MSE,对于较大的误差,它的行为则类似于MAE(Mean Absolute Error)。在实践中,Huber损失对于噪声(异常值)具有很强的鲁棒性。
-
对数损失(Log Loss):对数损失也叫做逻辑损失或交叉熵损失,是二分类问题中最常用的损失函数之一。
-
CTC(Connectionist Temporal Classification):CTC损失函数用于序列任务,如语音识别或手写识别,其中输入的序列长度与输出的序列长度可能不匹配。
损失函数使用原则
1、损失函数衡量神经网络模型在执行特定任务时的好坏程度。为了使神经网络更好,我们必须在反向传播步骤中最小化损失函数的值。
2、当使用神经网络预测概率时,只在分类任务中使用交叉熵损失函数。
3、对于回归任务,想让网络预测连续数时,就必须使用均方误差损失函数。
4、我们在需求预测期间使用平均绝对百分比误差损失函数来关注网络在训练期间的性能。
激活函数
激活函数和损失函数的区别
- 损失函数(Loss Function) ,也叫成本函数,主要用来衡量模型预测结果和真实结果之间的差距。模型训练的目的就是要通过优化算法(如梯度下降)使得损失函数的值尽可能的小。常见的损失函数有均方误差(MSE),交叉熵(Cross Entropy)等。
- 激活函数(Activation Function) 是用来给神经元添加一些非线性因素,使得神经网络可以逼近任何复杂函数,提高神经网络模型的表达能力。通常来讲,激活函数会被应用在每个神经元的输出上。知名的激活函数包括ReLU (Rectified Linear Unit),Sigmoid,TanH,Softmax等。
损失函数用于衡量模型的预测能力,而激活函数用于增强模型的表达能力。
激活函数Relu-隐藏层
ReLU是目前最常用的激活函数之一,ReLU函数非常快速且简单,数值范围从0到正无穷,可以避免和降低梯度消失问题。其公式如下:f(x) = max(0, x)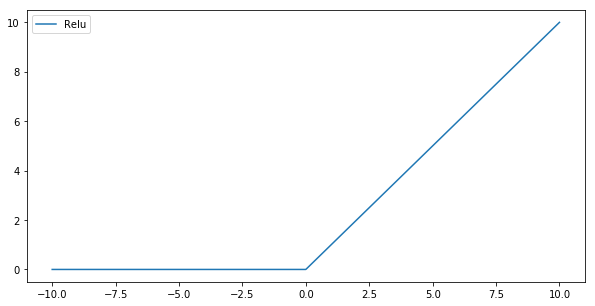
ReLU的优点是收敛快,求梯度简单。ReLU函数有助于实现快速收敛,因此模型训练速度很快。计算本质上线性函数的导数也更快。
问题在于函数的常量部分,这也是梯度为零的地方。梯度下降过程无法继续,模型的训练停止。
学习率调整将缓解这个问题。
ReLU 是一种常用的激活函数,特别是在深度神经网络中。它的形式是 f(x) = max(0, x),意味着当输入小于0时,输出是0;当输入大于0时,输出等于输入。
ReLU **函数的优点:**简单、计算高效,并且在输入为正数时梯度不会饱和,有利于网络的训练。
缺点:ReLU 函数在输入为负数时梯度为0,可能会导致一些神经元不再更新,这被称为"死亡ReLU"问题
激活函数Sigmoid和Tanh-隐藏层
Sigmoid函数
Sigmoid函数可以将任何范围的数值映射到0和1之间,对于二分类问题常常用于输出层。其公式如下:
f(x) = 1 / (1 + e^-x)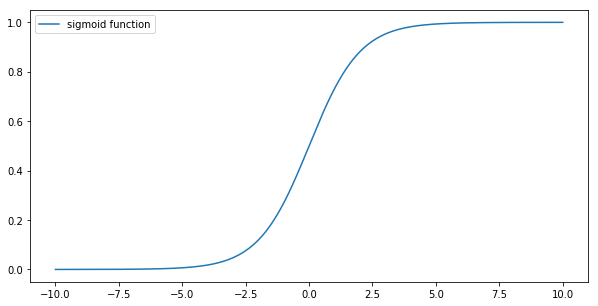
函数很快变平(值变为 0 或 1)。这也会导致偏导数很快为零,从而导致权重无法更新并且模型无法学习。这可以通过适当的权重初始化来缓解。
缺点:Sigmoid 函数在输入值较大或较小的情况下梯度接近于0,可能导致梯度消失问题,使网络难以训练。
Tanh(双曲正切)
它将数值映射到-1和1之间,使得输出以0为中心,常常用于隐藏层。其公式如下:
f(x) = (e^x - e^-x) / (e^x + e^-x)
Tanh 可以被认为是缩放的 sigmoid 函数,并且与原始 sigmoid 函数具有类似的梯度问题。调整权重将抑制梯度消失的模型问题。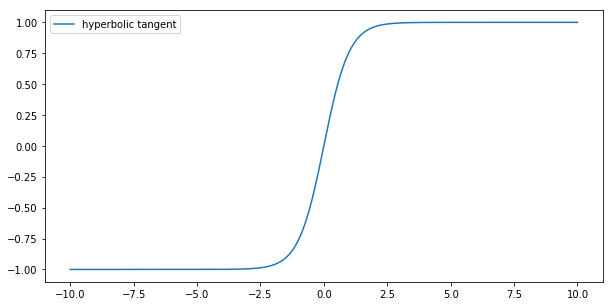
softmax激活函数-输出层
Softmax函数确实是一种激活函数,更准确地说,它是一种“归一化指数函数”。
Softmax函数一般应用在神经网络的输出层。具体来说,在分类问题中,Softmax函数常被应用于多分类模型的输出层,如,逻辑回归,多层感知机,卷积神经网络(CNN)和循环神经网络(RNN)等。它可以计算出一个概率分布,为每个类别生成一个概率值。这些概率加起来总和为1,最高的概率值对应的类别就是模型的预测结果。
总结
本篇博客分别解释了梯度,损失函数,激活函数等相关概念。前期概念准备部分基本结束,接下来我们就尝试自定义一个神经网络,实现训练,推理和生成模型等,也算是对基础概念部分的一个实践。
end