目录

1.摩尔定律放缓

2.Chiplet的优势

2.1 提升芯片良率、降本增效

2.2 设计灵活，降低设计成本

2.3 标准实行，构建生态

3.Chiplet如何上车

---

22年8月左右，Chiplet概念突然在二级市场火了起来，封测四小龙华天、长电、通富微电、晶方也因此赶上一波小反弹，当时只顾着哐哐买入，连Chiplet的基本概念也没有；并且由于认为Chiplet离汽车产品领域还很远，就不太关注。

不过最近看到瑞萨关于这方面的Blog出现，勾起了我的兴趣。在23年11月左右，瑞萨预先公布了第五代R-Car SoC的相关信息，该SoC面向高性能应用，采用先进的Chiplet小芯片封装集成技术，将为车辆工程师在设计时带来更大的灵活度。

瑞萨还分享了即将推出的两款MCU产品规划：一款为全新跨界MCU系列，旨在为下一代汽车E/E架构中的域和区域电子控制单元（ECU）打造所需的高性能，这款产品将缩小传统MCU与先进R-Car SoC间的性能差距；瑞萨同时还将发布一款为车辆控制应用量身定制的独立MCU平台。如下图所示：

很明显，事情变得复杂了起来，第4代产品我们还在追赶，第五代已经蓄势待发了。

那么要了解产品，首先就先来了解了解技术：Chiplet到底是什么东西？为什么这股风吹到了汽车芯片行业？

1.摩尔定律放缓

摩尔定律由戈登·摩尔提出，核心内容为“当价格不变时，集成电路上可容纳的晶体管的数目，约每隔18-24个月便会增加一倍。”也就是说处理器性能大约每两年翻一倍，同时价格下降一半。

但实际上，随着工艺制程推进到5nm、3nm等级别，物理上的极限也已经基本到顶了，换句话说，再往前推进到1nm甚至埃米级别，所需要付出的成本代价呈指数级上升。

据安信证券总结，Wafer价格和Die的花费已经脱离了摩尔定律。

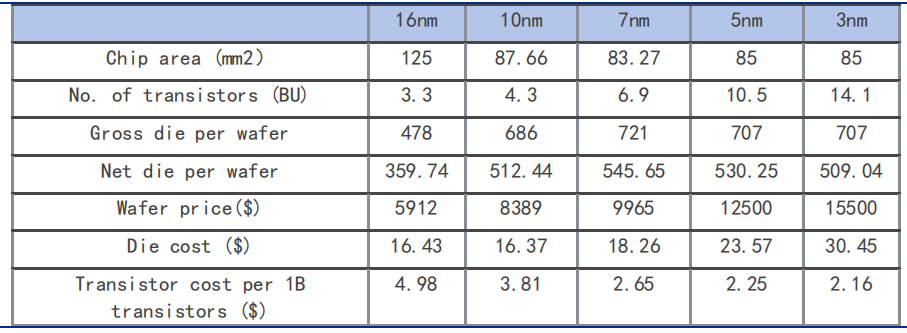
 因此，在单SoC向更高级别制程推进受阻时，以Chiplet异构集成的先进封装技术延续了摩尔定律。

Chiplet 中文名芯粒，通俗讲，通过将原来集成于同一SoC中的各个元件分拆，独立为多个特定功能的Chiplet，分开制造后再通过先进封装技术将彼此互联，最终封装为一个系统芯片。

这和搭乐高积木异曲同工，既可以将一颗大芯片拆解设计成几颗与之有相同制程的小芯片，也可以将其拆解设计成几颗拥有不同制程的小芯片。如下图：

很明显，这种技术是用在高算力的SoC，重点关注智驾、座舱等领域（目前MCU在工艺制程28nm已经是比较先进了），举例来说，若高级驾驶辅助系统（ADAS）需要兼顾更突出的AI性能时，工程师可将AI加速器集成至单个芯片中。