归并排序
- 1. 基本思想
- 2. 数据的分解
- 3. 数据的合并
- 4.归并排序的实现
- 4.1 递归实现
- 4.1.1 一个易错点
- 4.1.2 运行结果
- 4.2 非递归实现
- 4.2.1 图示思路
- 4.2.2 代码实现
- 4.2.3 一个易错点
- 4.2.4 修改后的代码
- 4.2.5 运行结果
- 6. 时间复杂度
- 7. 空间复杂度
- 8. 稳定性
- 9. 动图演示
1. 基本思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
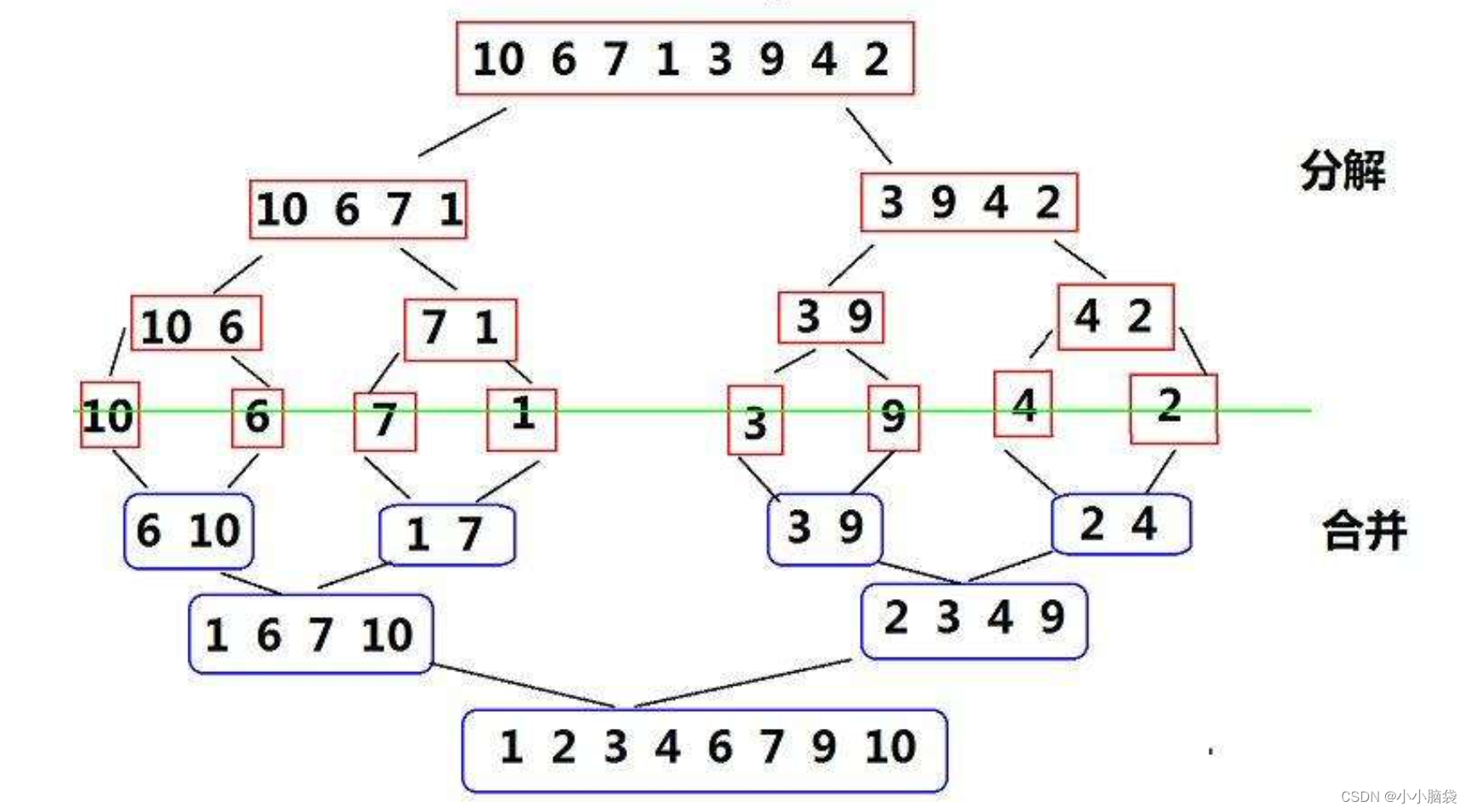
2. 数据的分解
数据的分解采用递归分解,形式上和一棵完全二叉树相似。

3. 数据的合并
数据的合并过程不仅仅是将短数据合成长的,否则这仅仅是原来分解数据的逆过程。数据的合并过程中牵扯到对两组数据的排序再合并。为了实现这一目的,采用了双指针法。下面以图1.1中的
两组数据为例进行说明;

4.归并排序的实现
4.1 递归实现
/*** 归并排序* 时间复杂度:O(n*logn)* 空间复杂度:O(n)* 稳定性:稳定* @param array*/public static void mergeSort(int[] array){//为了使参数只有一个,保持统一性,调用了mergeFunc()方法mergeFunc(array,0, array.length-1);}public static void mergeFunc(int[] array,int left,int right){if(left >= right){return;}int mid = left + (right - left) / 2;mergeFunc(array,left,mid); //分解左边mergeFunc(array,mid+1,right);//分解右边//开始合并merge(array,left,mid,right);}public static void merge(int[] array,int left,int mid,int right){int s1 = left;int e1 = mid;int s2 = mid+1;int e2 = right;int[] tmpArray = new int[right - left + 1];int k = 0;//1.保证两个数组都有数据while(s1 <= e1 && s2 <= e2){if(array[s1] < array[s2]){tmpArray[k] = array[s1];k++;s1++;}else{tmpArray[k] = array[s2];k++;s2++;}}//2.其中一个数组已经拷贝完,将另一个数组剩下的部分拷贝回临时数组while(s1 <= e1){tmpArray[k] = array[s1];k++;s1++;}while(s2 <= e2){tmpArray[k] = array[s2];k++;s2++;}//3.将临时数组中的数据拷贝回原数组中for(int i = 0;i < k;i++){array[left + i] = tmpArray[i];//这一步array[]的下标要注意}}
4.1.1 一个易错点
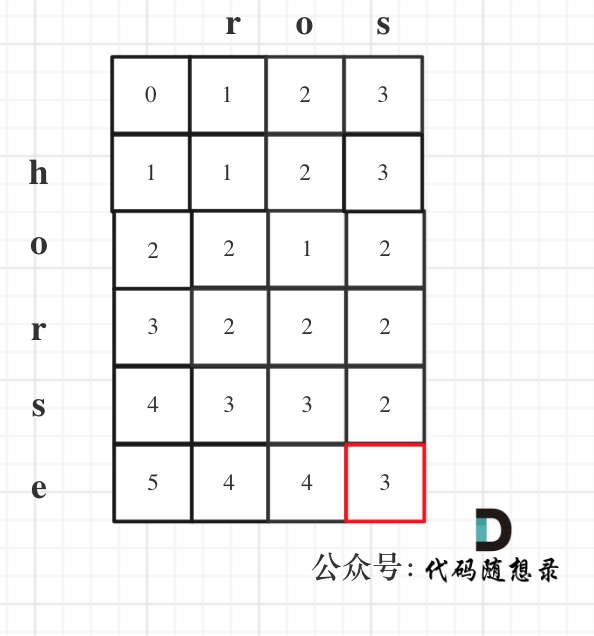
在将临时数组tmpArray[]中的数据放回原数组array[]的过程中,要特别注意下标问题。如图:

黄线框里的代码不能写成array[i] = tmpArray[i]。以一张图说明:

4.1.2 运行结果
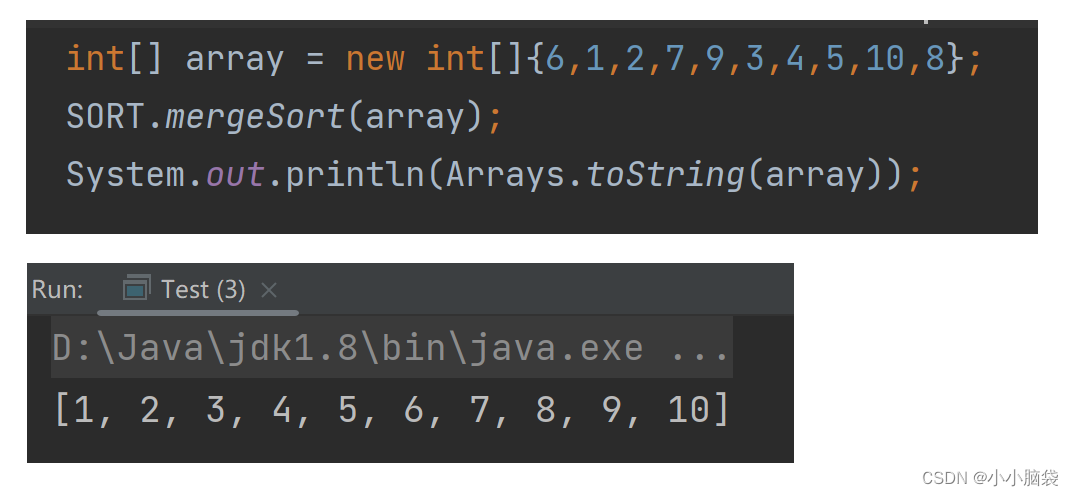
4.2 非递归实现
4.2.1 图示思路

4.2.2 代码实现
/*** 并排序(非递归实现)* @param array*/
public static void mergeSortNotRecursion(int[] array){//为了使参数只有一个,保持统一性,调用了mergeFunc()方法int gapNumber = 1; //gapNumber表示每组数据的个数//最外层控制组数while(gapNumber < array.length){for(int i = 0;i < array.length;i += gapNumber){//i每次走gapNumber个距离int left = i;int mid = left + gapNumber - 1;int right = mid + gapNumber;merge(array,left,mid,right);}gapNumber *= 2;}}public static void merge(int[] array,int left,int mid,int right){int s1 = left;int e1 = mid;int s2 = mid+1;int e2 = right;int[] tmpArray = new int[right - left + 1];int k = 0;//1.保证两个数组都有数据while(s1 <= e1 && s2 <= e2){if(array[s1] < array[s2]){tmpArray[k] = array[s1];k++;s1++;}else{tmpArray[k] = array[s2];k++;s2++;}}//2.其中一个数组已经拷贝完,将另一个数组剩下的部分拷贝回临时数组while(s1 <= e1){tmpArray[k] = array[s1];k++;s1++;}while(s2 <= e2){tmpArray[k] = array[s2];k++;s2++;}//3.将临时数组中的数据拷贝回原数组中for(int i = 0;i < k;i++){array[left + i] = tmpArray[i];//这一步array[]的下标要注意}}
4.2.3 一个易错点

4.2.4 修改后的代码
while(gapNumber < array.length){for(int i = 0;i < array.length;i += gapNumber){//i每次走gapNumber个距离int left = i;int mid = left + gapNumber - 1;if(mid >= array.length){mid = array.length - 1;}int right = mid + gapNumber;if(right >= array.length){right = array.length - 1;}merge(array,left,mid,right);}gapNumber *= 2;}
4.2.5 运行结果

6. 时间复杂度
整个归并排序的过程相当于一棵完全二叉树的创建过程。假设待排序的数据的容量为n,则完全二叉树的高度为log2(n+1)(向上取整),每一层遍历n个数据,最终用时nlog2(n+1),故最终的时间复杂度为O(nlog2(n))。
7. 空间复杂度
由于每次归并两组数据的过程中都借用了临时数组tmpArray[],且tmpArray[]的长度至少要等于两组数据的元素个数之和,故最终的空间复杂度为O(n)。
8. 稳定性
归并排序是一种稳定排序。
9. 动图演示











![[OpenAI]继ChatGPT后发布的Sora模型原理与体验通道](https://img-blog.csdnimg.cn/direct/6f21b60b46e84e9aaec5932e802046ae.jpeg)