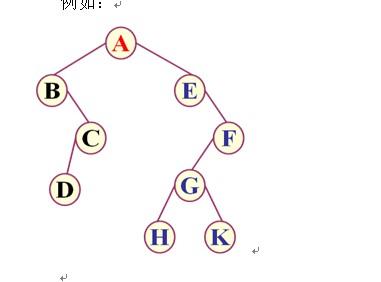
什么是中序遍历?
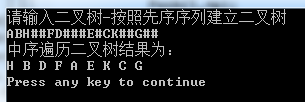
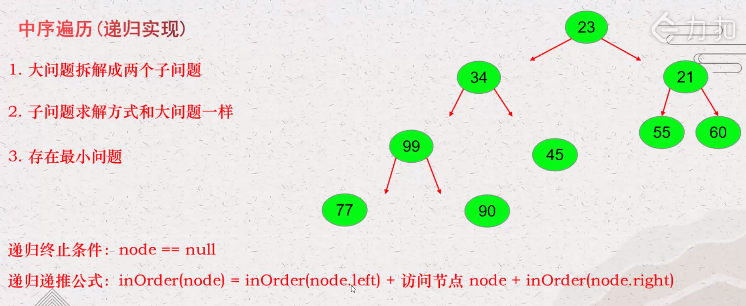
优先访问当前节点的左子树,然后访问当前节点,最后访问当前节点的右子树。
代码实现:
主要分为三部分:
1. 声明一个内部类,表示树的节点。
private class TreeNode<K,V> implements Map.Entry<K,V> { private K key; private V value; public TreeNode<K,V> left; public TreeNode<K,V> right; public TreeNode(K key, V value) { this.key = key; this.value = value; } @Override public K getKey() { return key; } @Override public V getValue() { return value; } @Override public V setValue(V value) { this.value = value; return value; } @Override public String toString() { return "TreeNode{" + "key=" + key + ", value=" + value + '}'; } }
2. 实现一个创建树的方法,通过对这个方法输入节点列表,生成对应的树结构。
public void createTree(List<K> keys, List<V> values) throws Exception { Queue<TreeNode<K,V>> queue = new LinkedList<TreeNode<K,V>>(); // 如果两个列表大小不一样或者为空,抛出异常 if (keys.size() != values.size() && keys.isEmpty() && values.isEmpty()) throw new Exception("Inputs' scale are not equal."); // 如果root为空,创建root if (root == null) root = new TreeNode<K,V>(keys.get(0), values.get(0)); TreeNode<K,V> p = root; // 创建树结构 for (int i = 1; i < keys.size(); i ++) { // 如果节点为空,寻找下一个不为空的节点,回滚i的值 if (p == null && !queue.isEmpty()) { p = queue.poll(); i --; continue; } if (p.left == null) { p.left = new TreeNode<K,V>(keys.get(i), values.get(i)); queue.offer(p.left); } else if (p.right == null) { p.right = new TreeNode<K,V>(keys.get(i), values.get(i)); queue.offer(p.right); } else { if (!queue.isEmpty()) { // 如果节点有左右子树,寻找下一个节点,回滚i的值 p = queue.poll(); i --; } } } }
3. 实现中序遍历方法。
递归版本:
// 中序遍历 递归 public void inorderRecursion(TreeNode<K,V> parent) { if (parent == null) return; inorderRecursion(parent.left); System.out.println(parent.toString()); inorderRecursion(parent.right); }
非递归版本:
先把当前节点的左子树都压栈,然后再获取右节点,再对右节点的左子树都压栈。
// 中序遍历 非递归 public void inorder() { if (root == null) return; Stack<TreeNode<K,V>> stack = new Stack<TreeNode<K,V>>(); TreeNode<K,V> p = root; while (p != null) { stack.push(p); p = p.left; while (p == null && !stack.isEmpty()) { p = stack.pop(); System.out.println(p.toString()); p = p.right; } } }
整个Tree类的代码(使用了泛型声明):
package Util; import java.util.*; public class Tree<K,V> { private TreeNode<K, V> root; public void createTree(List<K> keys, List<V> values) throws Exception { Queue<TreeNode<K,V>> queue = new LinkedList<TreeNode<K,V>>(); // 如果两个列表大小不一样或者为空,抛出异常 if (keys.size() != values.size() && keys.isEmpty() && values.isEmpty()) throw new Exception("Inputs' scale are not equal."); // 如果root为空,创建root if (root == null) root = new TreeNode<K,V>(keys.get(0), values.get(0)); TreeNode<K,V> p = root; // 创建树结构 for (int i = 1; i < keys.size(); i ++) { // 如果节点为空,寻找下一个不为空的节点,回滚i的值 if (p == null && !queue.isEmpty()) { p = queue.poll(); i --; continue; } if (p.left == null) { p.left = new TreeNode<K,V>(keys.get(i), values.get(i)); queue.offer(p.left); } else if (p.right == null) { p.right = new TreeNode<K,V>(keys.get(i), values.get(i)); queue.offer(p.right); } else { if (!queue.isEmpty()) { // 如果节点有左右子树,寻找下一个节点,回滚i的值 p = queue.poll(); i --; } } } } public TreeNode<K,V> getRoot() { return root; } // 中序遍历 递归 public void inorderRecursion(TreeNode<K,V> parent) { if (parent == null) return; inorderRecursion(parent.left); System.out.println(parent.toString()); inorderRecursion(parent.right); } // 中序遍历 非递归 public void inorder() { if (root == null) return; Stack<TreeNode<K,V>> stack = new Stack<TreeNode<K,V>>(); TreeNode<K,V> p = root; while (p != null) { stack.push(p); p = p.left; while (p == null && !stack.isEmpty()) { p = stack.pop(); System.out.println(p.toString()); p = p.right; } } } private class TreeNode<K,V> implements Map.Entry<K,V> { private K key; private V value; public TreeNode<K,V> left; public TreeNode<K,V> right; public TreeNode(K key, V value) { this.key = key; this.value = value; } @Override public K getKey() { return key; } @Override public V getValue() { return value; } @Override public V setValue(V value) { this.value = value; return value; } @Override public String toString() { return "TreeNode{" + "key=" + key + ", value=" + value + '}'; } } }
测试代码:
使用Junit进行测试,测试代码如下:
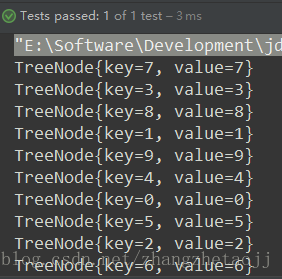
@Test public void inorderTest() throws Exception { List<Integer> keys = new ArrayList<Integer>(); List<String> values = new ArrayList<String>(); for (int i = 0; i < 10; i ++) { keys.add(i); values.add(i + ""); } Tree<Integer, String> tree = new Tree<Integer, String>(); tree.createTree(keys, values); tree.inorderRecursion(tree.getRoot()); tree.inorder(); }
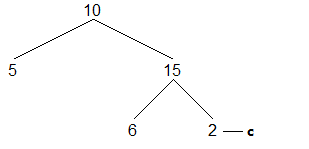
创建的树的结构:
测试结果:
相关文章:
二叉树遍历系列--前序遍历
二叉树遍历系列--中序遍历
二叉树遍历系列--后序遍历
二叉树遍历系列--层次遍历