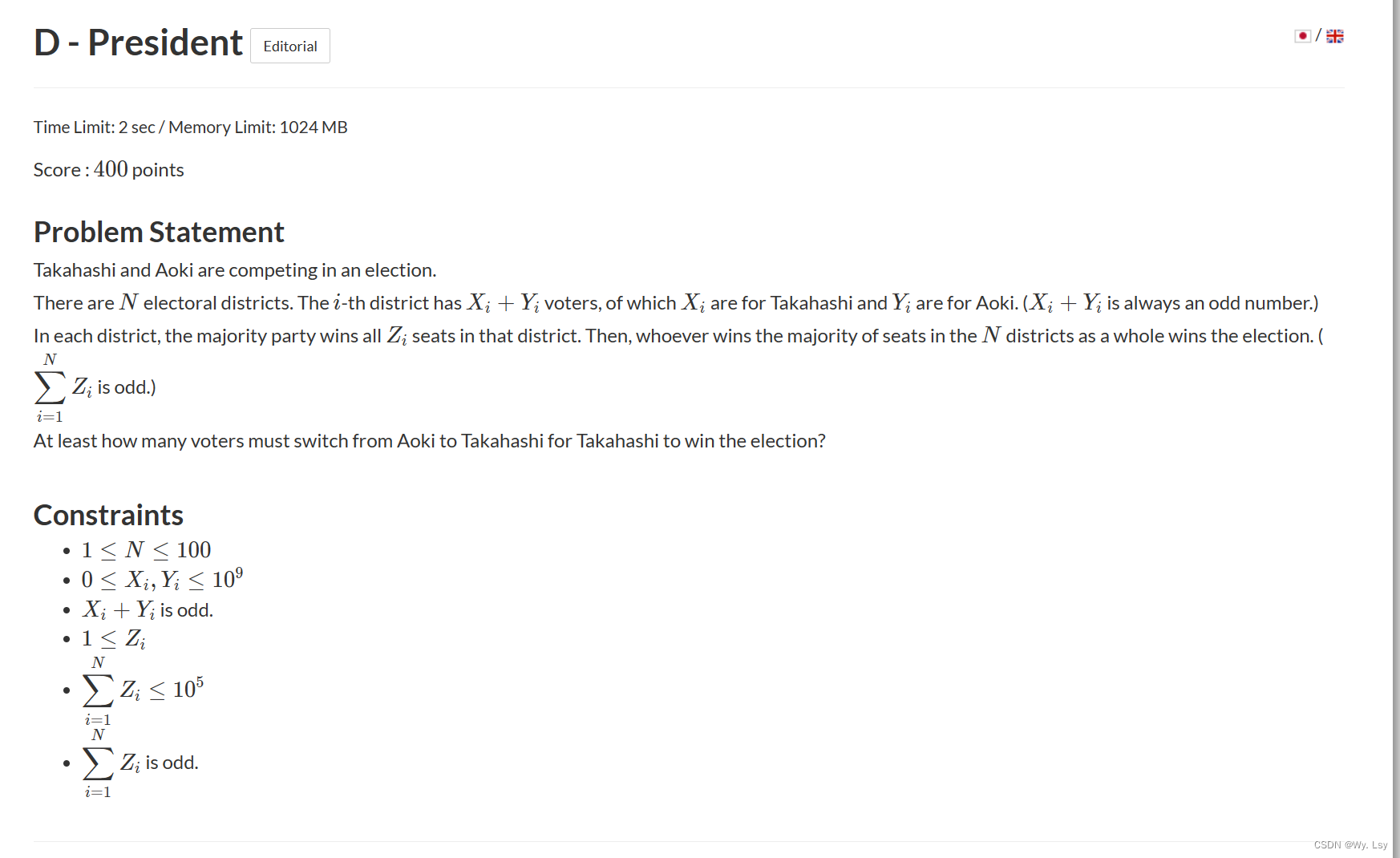
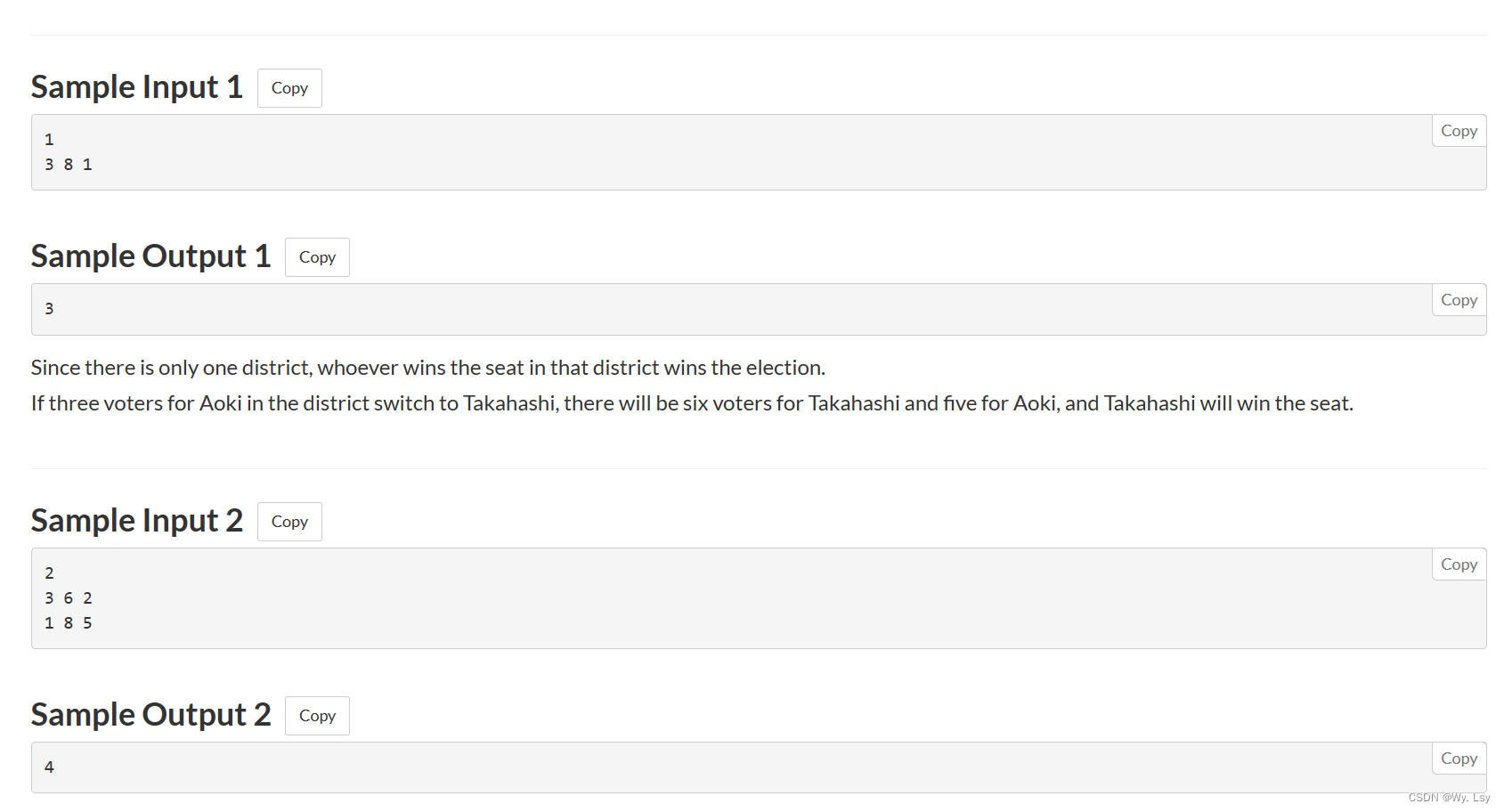
分析：

        需要让所有x大于y的对应的z的总数大于z总共的数量的一半，找最小需要转化的数量，那么可以转化为01背包问题，z作为体积，每组的x和y都可以计算出一个值表示需不需要转化，作为背包价值，如果x大于y那么一定价值是0，否则至少需要(y - x) / 2 + 1数量转化，那么就转化成了背包dp，然后因为只要大于等于z总数的一半都可以符合，所以最后对满足的所有情况取最小值。

代码：

       

#include <bits/stdc++.h>using namespace std;
using ll = long long;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n;cin >> n;vector<ll> x(n + 1), y(n + 1), z(n + 1);ll m = 0;for(int i = 1; i <= n; i ++) {cin >> x[i] >> y[i] >> z[i];m += z[i];}vector<ll> f(m + 1, 1e17);f[0] = 0;for(int i = 1; i <= n; i ++) {ll w = 0;if(y[i] > x[i]) w = (y[i] - x[i]) / 2 + 1;for(int j = m; j >= z[i]; j --) {f[j] = min(f[j], f[j - z[i]] + w);}}ll ans = 1e17;for(int i = m / 2 + 1; i <= m; i ++) ans = min(ans, f[i]);cout << ans << '\n';
}