
路径优化相关文章
- 1、路径优化历史文章
- 2、路径优化丨带时间窗和载重约束的CVRPTW问题-改进遗传算法:算例RC108
- 3、路径优化丨带时间窗和载重约束的CVRPTW问题-改进和声搜索算法:算例RC108
- 4、路径优化丨复现论文-网约拼车出行的乘客车辆匹配及路径优化
- 5、多车场路径优化丨遗传算法求解MDCVRP问题
- 6、论文复现详解丨多车场路径优化问题:粒子群+模拟退火算法求解
- 7、路径优化丨复现论文外卖路径优化GA求解VRPTW
- 8、多车场路径优化丨蚁群算法求解MDCVRP问题
- 9、路径优化丨复现论文多车场带货物权重车辆路径问题:改进邻域搜索算法
- 10、多车场多车型路径问题求解复现丨改进猫群算法求解
- 11、带时间窗车辆路径问题论文复现:改进粒子群算法求解
带时间窗的车辆路径问题
可描述为:车场有若干车辆、存在若干需求点、车辆从车场往返服务需求点。其中:车辆存在装载体积约束,数量约束,车辆在时间窗之外有惩罚成不。本文假设:
(1)物流配送中心数量单一,且配送中心的货物数量足够,不存在缺货现象;
(2)物流配送中心具有一定数量的同种类型车辆;
(3)各个客户点的地理位置、所需货物数量、时间窗限制等基本信息已知;
(4)配送车辆只负责将货物送至给顾客,不提供换货及退货服务;
(5)配送车辆的速度随路况的变化而变化。
详细描述见参考文献
数学模型
具体模型见参考文献,目标函数是不变成本和可变成本之和。不变成本是每辆车的固定成本,可变成本是每辆车的运行成本,和经过的客户点有关系。


文献没给Ei和Li的具体值,只计算了c1,c2,c3,没计算满意度
数据
论文数据,23个客户,复制数据到excel:

代码运行环境
windows系统,python3.6.0,第三方库及版本号如下:
numpy==1.18.5
matplotlib==3.2.1
第三方库需要在安装完python之后,额外安装,以前文章有讲述过安装第三方库的解决办法,点击下方文章名字跳转:
-
1、代码运行环境说明
-
2、第三方库安装方法
编码解码
编码
编码生成: 随机打乱客户编号
解码
一个车辆的解码如下:
1、 读出各车辆客户经纬度,货物体积,服务时间,时间窗;
2、 编码客户的第一个点时,计算车场到点的距离,其余点计算与上一个客户点的距离(经纬度距离乘111),根据车辆出发时间点取速度,根据速度计算时间,根据时间计算时间窗惩罚成本,更新运行成本,固定成本,惩罚成本;
3、每辆车遍历到最后一个点时,计算点到车场的距离,各项成本更新,解码结束:
代码如下:
def decode(self, road):road_car = [[]]every_tj = 0for ro in road:tj1 = self.tj[ro] # 对应客户点的体积if every_tj + tj1 <= self.V_max: # 如果添加新客户,能满足体积约束road_car[-1].append(ro) # 对应车辆添加客户点every_tj += tj1 # 更新车辆装载体积else: # 如果添加新客户,不满足体积约束road_car.append([ro]) # 新车辆添加添加客户点every_tj = tj1 # 更新车辆装载体积c_window = 0c1, c2 = 0, 0for rd in road_car:end_j = np.array(self.jd)[rd] # 一辆车对应的经度start_j = np.array([self.center[0]] + end_j.tolist()[:-1]) # 配送中心到倒数第二个点的经度end_w = np.array(self.wd)[rd] # 一辆车对应的纬度start_w = np.array([self.center[1]] + end_w.tolist()[:-1]) # 配送中心到倒数第二个点的纬度d_gab = np.sqrt((end_j - start_j)**2 + (end_w - start_w)**2)*111 # 车辆按顺序的两点之间距离t_start = self.t_begin # 起始时间count = 0for dg in d_gab:v_real = self.get_v(t_start) # 对应时间的运行速度t_start += dg/v_real # 到达时间idx = rd[count]if t_start < self.te[idx]: # 如果小于左时间窗,更新左时间窗成本c_window += (self.te[idx] - t_start)*self.ce if t_start > self.tl[idx]: # 如果大于左时间窗,更新右时间窗成本c_window += (t_start - self.tl[idx])*self.clt_start += self.tw[idx] # 更新时间(加对应客户点的服务时间)count += 1 # 客户点计数c2 += (count*self.g0 + self.gk) # 固定成本dij = sum(d_gab) + np.sqrt((end_j[-1] - self.center[0])**2 + (end_w[-1] - self.center[1])**2)*111 # 运输距离加上会配送中心的距离c1 += dij*self.c # 运输成本return road_car, c1 + c2 + c_window改进算法
粒子交叉

简单来说:选取父代编码相同长度的基因,初次交换;统计子代1与交换父代冲突的基因,子代2与父代冲突的基因,冲突基因再交换:
如上面的父代交换8,9,7,6 和2,5,6,7,得到子代1:[1,3,4,2,5,6,9,5,2],子代2:[4,8,3,8,9,7,6,7,1],子代1的冲突基因[2,5],子代2的冲突基因[8,7], 对应的冲突位置的基因再交换,即子代1的最后1个位置2换成,子代2的第2个位置的8;子代2的倒数第2个位置5换成,子代2的倒数第2个位置的7;
得到可行子代[1,3,4,2,5,6,9,7,8]和[4,2,3,8,9,7,6,7,1]
核心代码:
def cross(self, a, b):loc = random.sample(range(1, len(a)),2)loc.sort()idx1 = loc[0]idx2 = loc[1]a1 = a[:idx1-1] # 父代1前段a2 = a[idx2:] # 父代1后段b1 = b[:idx1-1] # 父代2前段b2 = b[idx2:] # 父代2后段aa = a[idx1-1:idx2] # 交换基因片段1bb = b[idx1-1:idx2] # 交换基因片段2aax,bbx = [], []for ax in aa: # 冲突基因1寻找if ax in b1 or ax in b2:bbx.append(ax)for bx in bb: # 冲突基因2寻找if bx in a1 or bx in a2: aax.append(bx)count = 0for au in aax: # 遍历冲突基因2if au in a1: # 如果冲突基因在父代1前段id1 = a1.index(au) # 找到冲突基因位置 bbxx = bbx[count] # 冲突基因1的交换基因if bbxx in b1: # 如果交换基因在父代2前段id2 = b1.index(bbxx) # 交换对应位置基因a1[id1], b1[id2] = b1[id2], a1[id1] # 交换对应位置基因if bbxx in b2: # 如果冲突基因在父代2后段id2 = b2.index(bbxx) # 交换基因位置a1[id1], b2[id2] = b2[id2], a1[id1] # 交换对应位置基因count += 1if au in a2: # 如果冲突基因在父代1后段,其余操作如上id1 = a2.index(au)bbxx = bbx[count]if bbxx in b1:id2 = b1.index(bbxx)a2[id1], b1[id2] = b1[id2], a2[id1]if bbxx in b2:id2 = b2.index(bbxx)a2[id1], b2[id2] = b2[id2], a2[id1]count += 1a = a1 + bb + a2 # 交换好的基因片段拼接b = b1 + aa + b2return a, b
粒子交叉
比较简单,随机生成2个位置,交换对应基因:
def mul(self, a):loc = random.sample(range(len(a)),2)idx1 = loc[0]idx2 = loc[1]a[idx1], a[idx2] = a[idx2], a[idx1] # 2个位置基因互换return a
粒子群算法
文献流程:
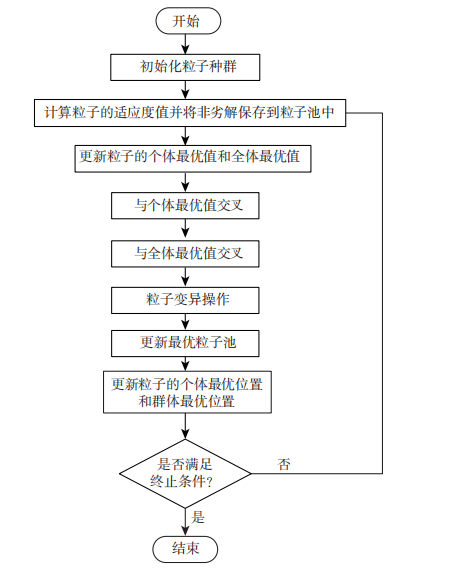
推文只有一个目标,具体的粒子群算法步骤如下:
(1)初始多个编码当做局部最优种群,初始多个编码当做迭代种群;
(2)迭代种群的个体与局部最优和全局最优进行交叉,然后自身进行变异;
(3)新解优于对应局部最优解时,更新局部最优解,另外更新迭代种群;
(4)根据局部最优解更新全局最优解;
(5)检查结束条件。若符合算法终止条件,则得到优化结果;否则,继续执行(2)
核心代码:
def total(self, num, generation, cd):ind_road = [cd.code() for i in range(num)] # 初始多个编码当局部最优种群ind_f = [cd.decode(road)[-1] for road in ind_road] # 对应的局部最优值best_idx = ind_f.index(min(ind_f)) # 全局最优索引gbest_road = ind_road[best_idx] # 全局最优路径T_road = [cd.code() for i in range(num)] # 随机多个编码当初始种群result = [[0],[min(ind_f)]]for gen in range(generation):for n in range(num):road = T_road[n]road_i = ind_road[n] # 局部最优值road1, _ = self.cross(road, road_i) # 局部最优交叉road2, _ = self.cross(road1, gbest_road) # 全局最优交叉road2 = self.mul(road2) # 变异if cd.decode(road2)[-1] < ind_f[n]: # 如果新解优与劣解ind_road[n] = road2 # 更新局部最优ind_f[n] = cd.decode(road2)[-1]T_road[n] = road2best_idx = ind_f.index(min(ind_f))gbest_road = ind_road[best_idx] # 全局最优更新result[0].append(gen+1)result[1].append(min(ind_f))return gbest_road, result
结果
主函数
设计主函数如下:
import pandas as pd
import numpy as np
from code_decode import co_de
from pso import psodf = pd.read_excel('数据1.xlsx', sheet_name = '坐标时间窗')
df1 = pd.read_excel('数据1.xlsx', sheet_name = '行驶速度')jd, wd, tj, tw, te, tl = df['经度'], df['纬度'], df['体积'], df['服务时间'], df['最早时间'], df['最晚时间'],
td, v = df1['时间段'], df1['速度']
parm_data = [jd, wd, tj, tw, te, tl, td, v]center = [113.8321, 34.703993] # 配送中心经纬度
V_max = 8 # 最大容纳体积
t_begin = 8
ce, cl = 5, 15 # 早到和晚到的单位时间窗成本
g0, gk = 40, 210 # 点位费和车辆的指派成本
c = 2.5 # 单位运行成本
parm_de = [center, V_max, t_begin, ce, cl, g0, gk, c]cd = co_de(parm_data, parm_de)
p = pso()
num, generation = 20, 13 # 种群规模
gbest_road, result = p.total(num, generation, cd) # 算法结果
road_car, f = cd.decode(gbest_road)
print('\n结果验证:', f)
print('\n路径:', road_car)cd.draw(road_car, f) # 画路径图
cd.draw_change(result) # 画成本变化
运行结果
结果如下:
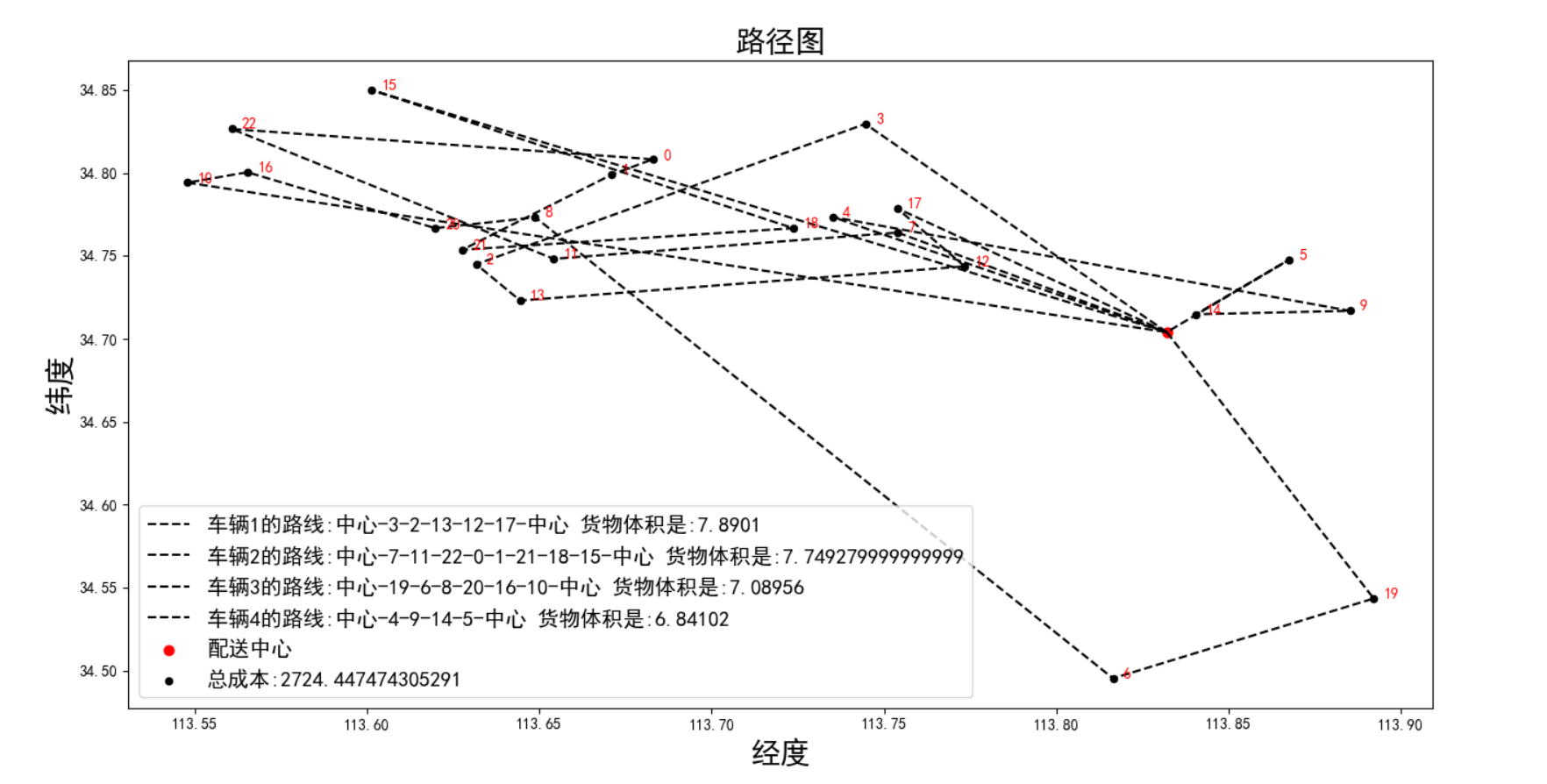
路径图:
成本随迭代次数的变化图如下:
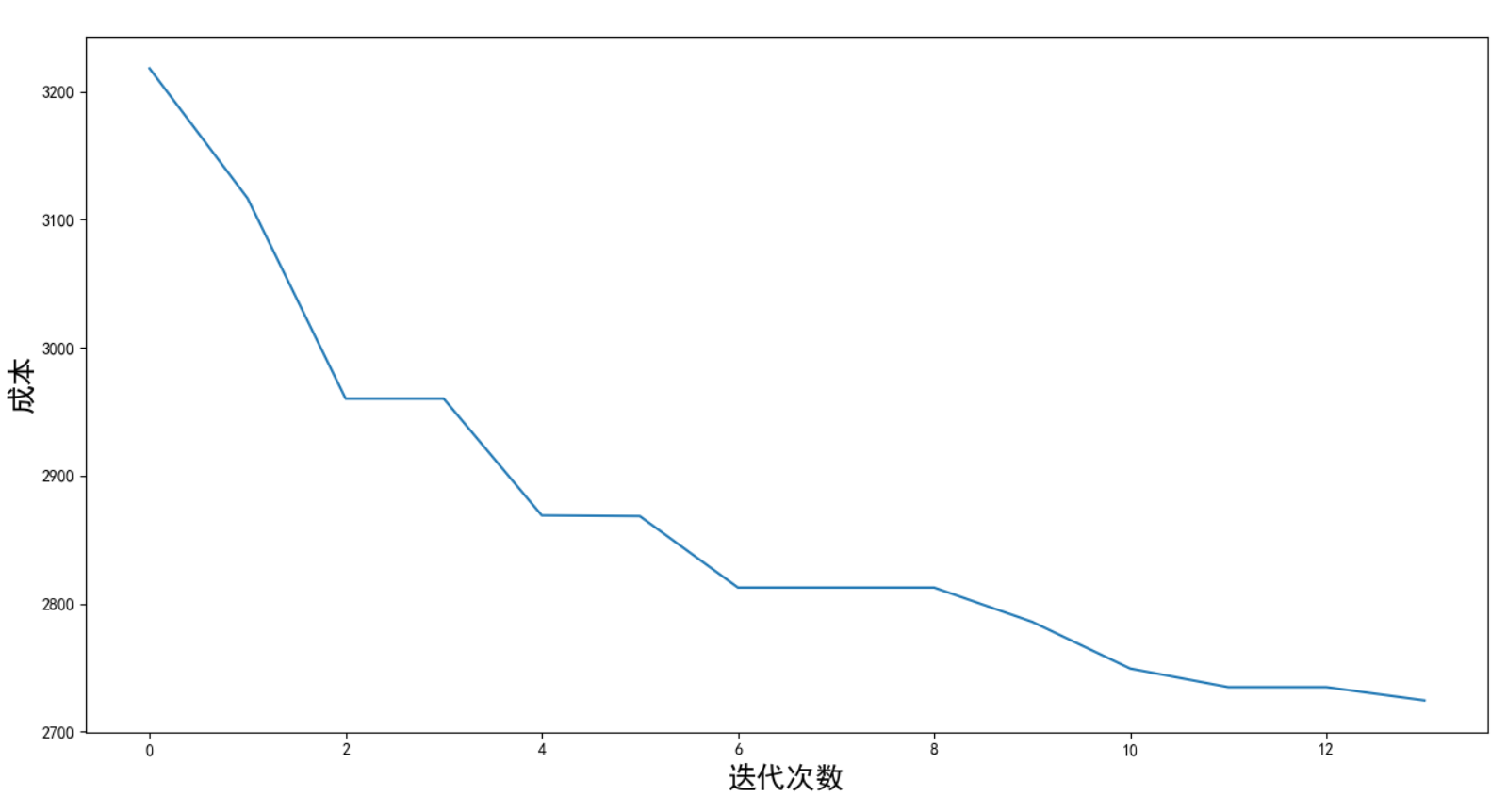
还有优化空间,增大种群规模和迭代次数试试。
结论
本推文主要是对参考论文进行复现,有小改动:因为文献也没有给出相关参数,所以没有计算满意度,变成单目标问题,如果感兴趣可以设计参数进行测试,比较容易。其余基本是复现原文,详细介绍了交换和变异算子,可视化也有一些自己设计。
数据和算法皆可修改(考虑运行时间,推文把一些运行参数调低)。
参考文献:基于多目标混合粒子群算法的车辆路径优化_李琦翔
代码
为了方便和便于修改和测试,把代码在3个py文件里。
演示视频:
路径优化丨复现论文-带时间窗车辆路径问题论文复现:改进粒子群算法求解
![[C/C++入门][进制原理]27、计算机种的进制](https://i-blog.csdnimg.cn/direct/1f14e02a572944768cec3eeaaeeb77ba.png)








![[数据分析]脑图像处理工具](https://i-blog.csdnimg.cn/direct/9dbc991daef44544b9146f147cad59b0.png)








