[C/C++入门][进制原理]27、计算机种的进制

各种信息进入计算机，都要转换成“0”和“1”的二进制形式。

计算机采用二进制的原因是：

物理上容易实现，可靠性高。（电子元件的通电和不通电就可以表示1和0，所以非常方便）
运算简单，通用性强。
便于表示和进行逻辑运算。

进位计数制的特点：

采用进位的方式进行计数；

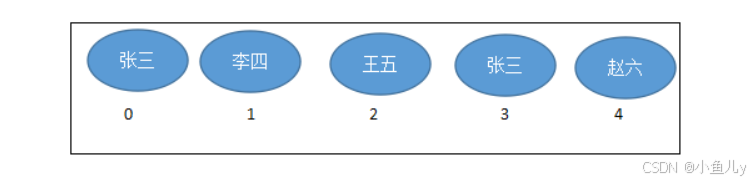
使用位置表示法

例如：

$123.45=1\times 10^{2} +2\times10^{1}+3\times10^{0}+4\times10^{-1}+5\times10^{-2}$

表 2-1 计算机中常用的数字系统进制

二进制

十进制

八进制

进制	二进制	十进制	八进制	十六进制
进位规则	逢二进一	逢十进一	逢八进一	逢十六进一
基数	2	10	8	16
基本符号	0,1	0,1,2, …,9	0,1,2, …,7	0,1,2, …,9,A,B,C,D,E,F

十进制转换成二进制123.45转1111011.011100

计算机种如何表示呢？

在C++中，你可以使用

进制表示

二进制 (0b 或 0B 前缀)：从C++11开始，你可以使用前缀0b或0B来表示二进制数。
```
int num = 0b1011; // 等同于十进制中的11
```
八进制 (0 前缀)：八进制数可以通过在数字前添加0来表示。
```
int num = 011; // 等同于十进制中的9
```

3.十进制：没有特殊前缀，默认就是十进制。

int num = 11; // 直接写数字

4.十六进制 (0x 或 0X 前缀)：十六进制数通过前缀0x或0X来表示。

int num = 0xB; // 等同于十进制中的11

输出进制转换

你可以使用std::cout结合std::dec, std::hex, std::oct和std::bitset来输出不同进制的数字。

十进制 (std::dec)：

std::cout << std::dec << num; // 输出十进制形式

十六进制 (std::hex)：

std::cout << std::hex << num; // 输出十六进制形式

八进制 (std::oct)：

std::cout << std::oct << num; // 输出八进制形式

二进制 (std::bitset)： std::bitset可以用来输出二进制字符串。

std::bitset<32> bits(num);
std::cout << bits << '\n'; // 输出二进制形式

输入进制转换

使用std::cin读取数字时，你可以指定进制，例如：

int num;
std::cin >> std::hex >> num; // 假设用户输入十六进制数字

各个进制：

#include <iostream>
#include <bitset>int main() {int num = 27;std::cout << "Decimal: " << num << '\n';std::cout << "Binary:   " << std::bitset<32>(num) << '\n';std::cout << "Octal:    " << std::oct << num << '\n';std::cout << "Hexadecimal: " << std::hex << num << '\n';return 0;
}