6.6 二元函数的极值_哔哩哔哩_bilibili
此笔记为听课笔记,宋浩老师微积分~
最近诸事缠身,会有种会不会只做一件事好些。实际上,关键在于动力,我不可能每次都准备充分。动力,分配,这是目前进入大学我正在学习的最宝贵的东西。
导数和微分的区别
1概念产生的背景不同,解决的问题不同
函数的变化率问题:导数的概念
函数的增量问题:微分的概念


45-6.4全微分
 证明
证明



全微分的重要应用是近似计算

可微的必要条件,充分条件


48-6.6二元函数的极值
极值的定义

极值存在的必要条件,充分条件

偏导=0的点叫做驻点
辨析:一元

无条件极值,条件极值
应用:优化模型
 将条件极值转化为无条件极值
将条件极值转化为无条件极值
¥?证明一下捏)拉格朗日乘数法——解决带条件的极值问题
z:目标函数,g:约束函数

【补】托马斯微积分CH15catalogue:multiple integrals
15.1Double and iterated over Rectangle
15.2Double Integrals over General Regions
15.3Area by Double Integration
15.4Double Integrals In Polar Form
15.5Triple Integrals in Rectanglar Form
15.6Applications
15.7Triple Integrals in cylindrical and Spherical Coordinates
15..8Sustitutions in Multiple Intergrals
49-6.7二重积分的定义和性质
二重积分的概念

按照直角坐标系分:
 (上图,靠右的分法为极坐标系分法)
(上图,靠右的分法为极坐标系分法)
二重积分的几何含义

辨析:还记得定积分把,拿来干嘛了。拿来求面积。二重积分拿来求体积了。
二重积分的性质


性质4的推论

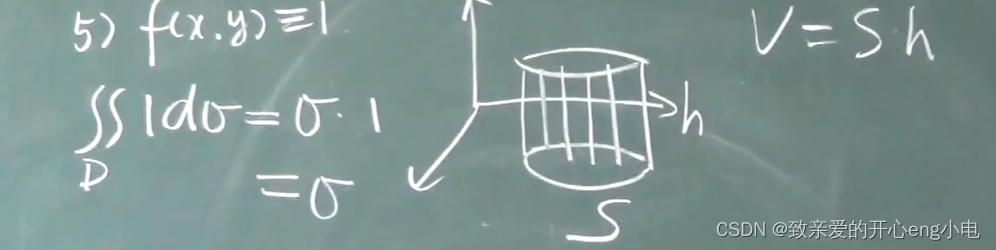
(三:恒等于)
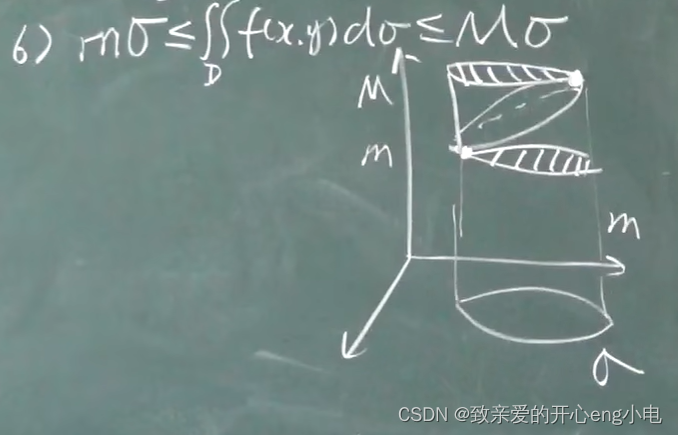
二重积分的中值定理

50-6.8二重积分的计算(直角坐标系

二重积分积完后只剩下一个variable
x:上边的减下边的;
y:右边的减左边的
特例

51-6.8二重积分的计算(极坐标)
极坐标的定义:



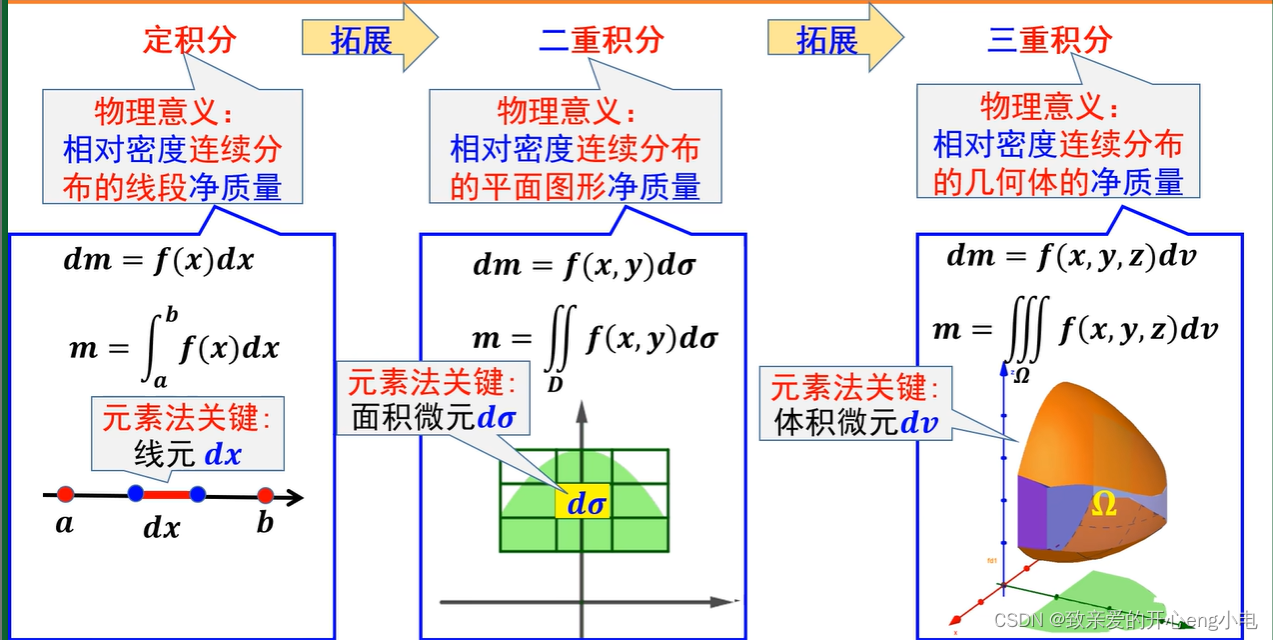
三重积分的基本概念(由定积分到拓展)
overlook:


三重积分的定义