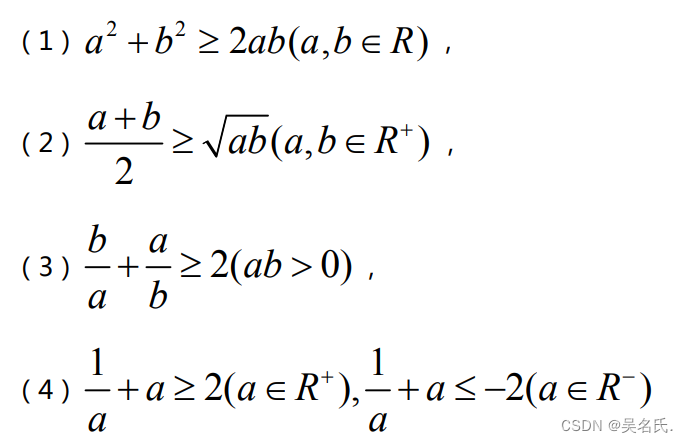一、函数
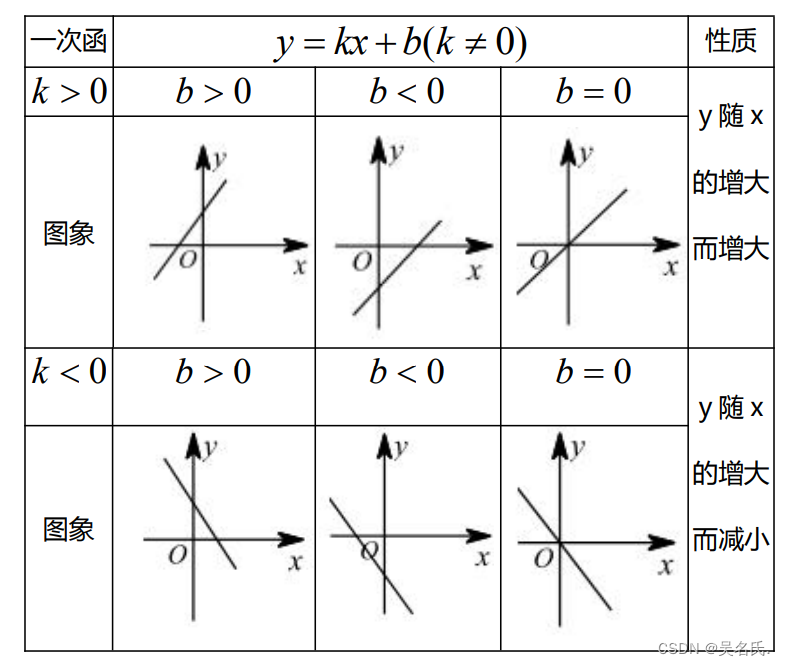
1.一次函数 y = kx + b(k≠0) 的图象及性质
2.二次函数y = ax^2 + bx + c的图象和性质
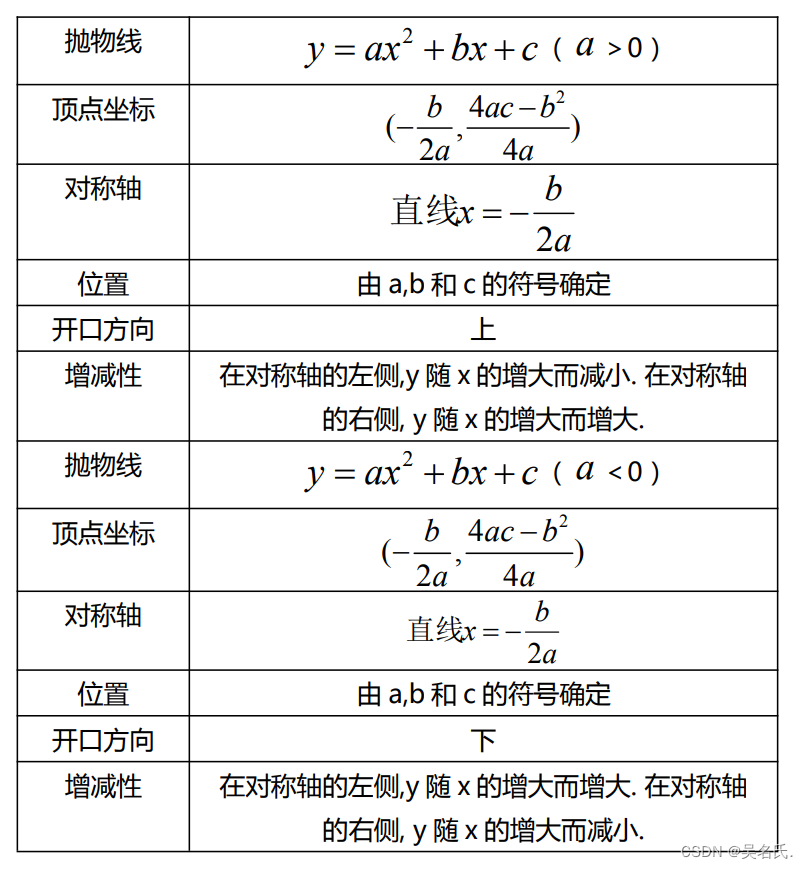
3.指数函数y = a^x ( a>0,且a≠1)的图象和性质
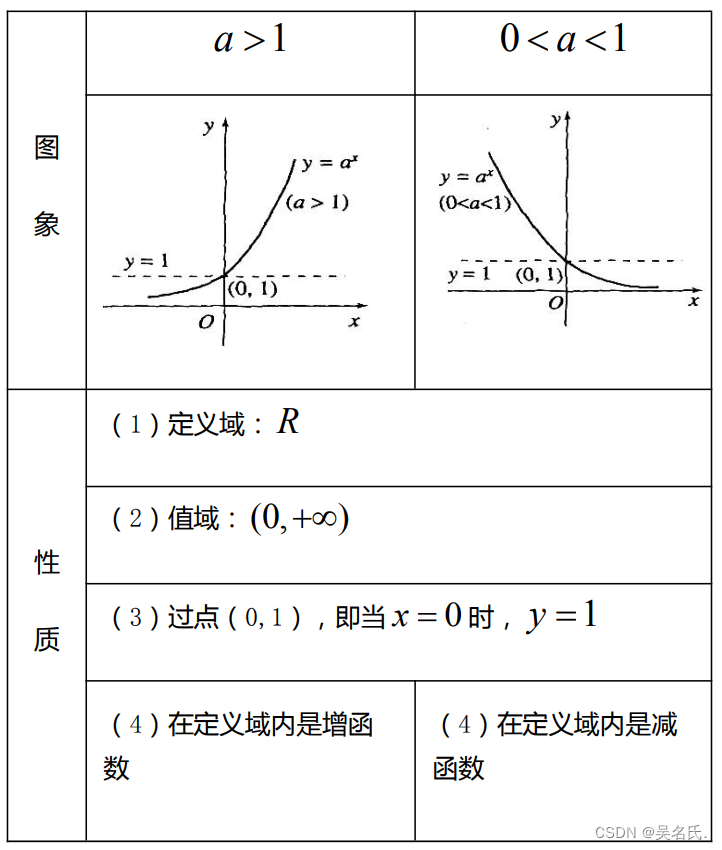
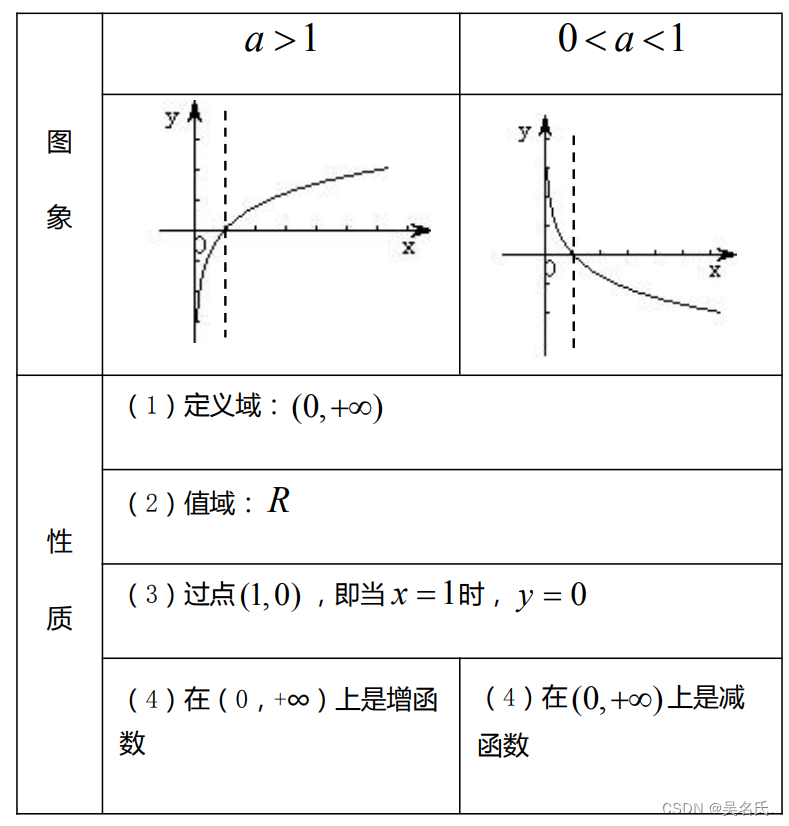
4.对数函数y =logₐx ( a>0,且a≠1)的图象与性质
二、方程
1.一元一次方程 ax +b=0(a≠0)
解法:x=-b/a
2.二元一次方程
解法:加减消元法,代入消元法等
3.一元二次方程ax^2 + bx + c = 0
(1)解法:
①分解因式
若 ax^2 + bx + c =a(x - x1)(x - x2) = 0(a ≠ 0),则x = x1 或 x = x2
②公式法
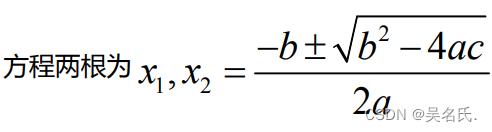
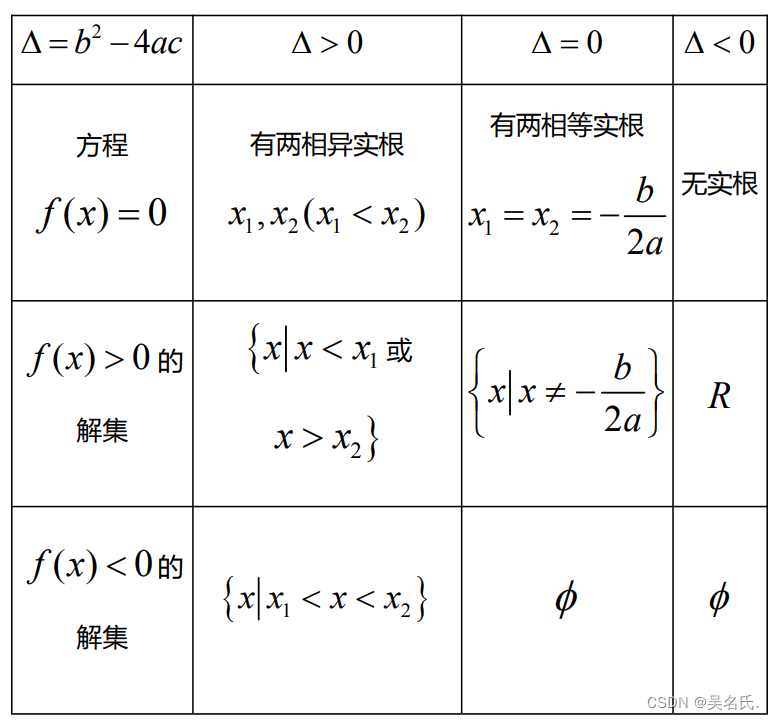
(2)根的判别式(△=b^2-4ac)
①当 △> 0 时,方程有两相异的实数根;
②当 △= 0 ,方程有两相等的实数根;
③当 △<0 时,方程没有实数根
(3)根与系数的关系(韦达定理)
①设方程ax^2 + bx + c = 0(a≠0)的两个根为x1和x2
则有如下结论:
x1 + x2 = -b / a
x1 * x2 = c / a
②韦达定理的应用
利用韦达定理求关于两个根的代数式的数值:
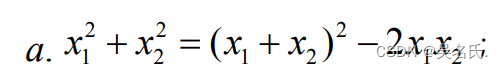
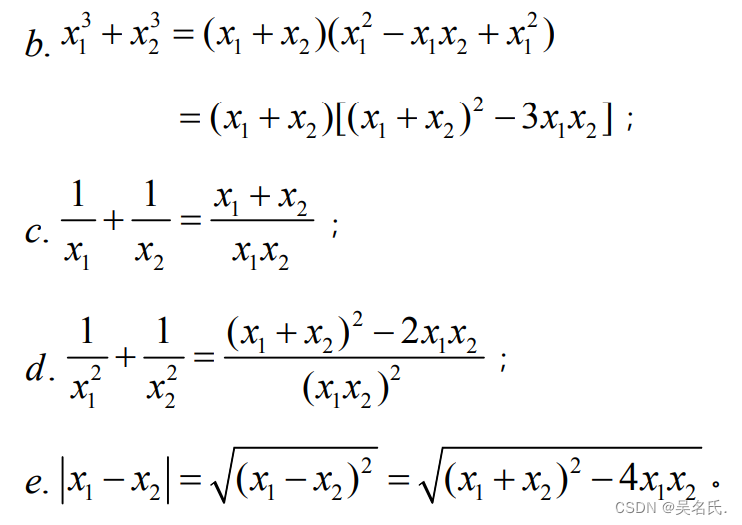
4.一元 n 次方程
形如 a(x - x1)(x - x2)…(x - xn) = 0 方程称为一元 n 次方程,x1、x2…xn是它的n个根
三、不等式
1.不等式的基本性质

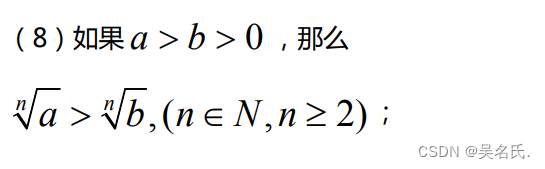
2.不等式的求解
(1)一元一次不等式 ax >b(或ax<b)
解不等式时,运用不等式的性质,去分母,去括号,移项,合并同类项,最后变为 x > c或 x < c
(2)一元一次不等式组
每个一元一次不等式的解集的公共部分(交集)叫做一元一次不等式组的解集
(3)绝对值不等式的解法
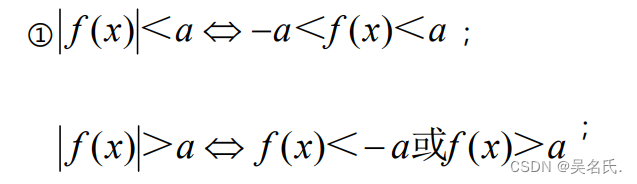

(4)一元二次不等式ax^2 + bx + c >0(a ≠ 0)
一元二次不等式的解法如下表,设f (x) = ax^2 + bx + c(a ≠ 0) :
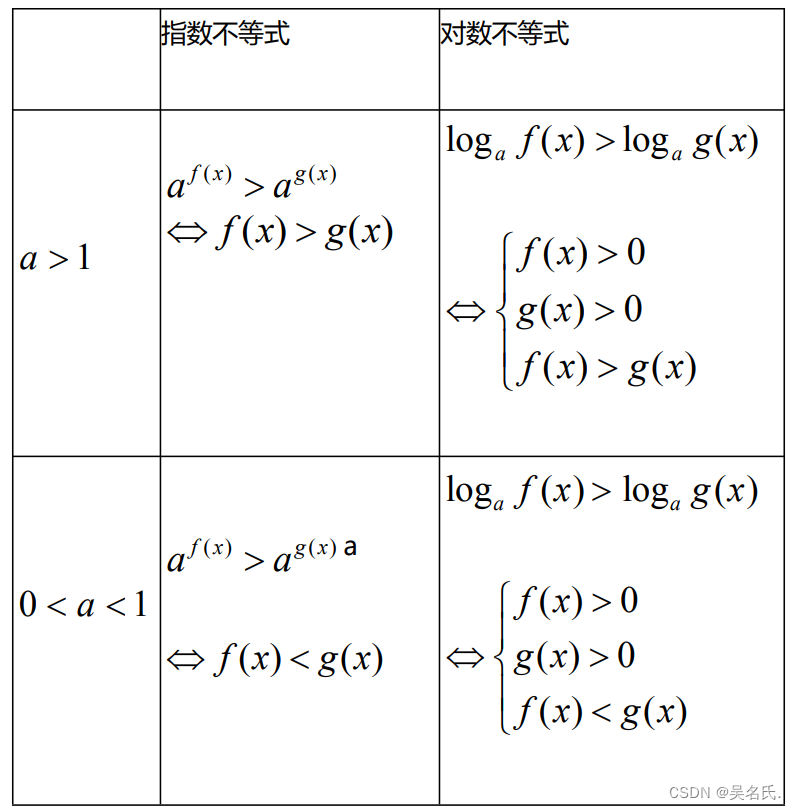
(5)指数、对数不等式
不等号两边同时取指数或同时取对数,变成相同的形式后,再换元成有理不等式求解:
3.常用的基本不等式