目录
一. 滤波器分类
二.卡尔曼滤波(Kalman Filter)原理
(1)定性理解
(2)定量推导
1. 预测阶段
2. 更新阶段
3. 卡尔曼增益
1)卡尔曼增益
2)如何理解卡尔曼增益?
三.统计概念理解
(1)马尔科夫链
(2)转移矩阵
四.卡尔曼滤波代码(matlab)
一. 滤波器分类
滤波是信号处理中的一个重要概念,滤波电路的作用是尽可能减小脉动的直流电压中的交流成分,保留其直流成分,使输出电压纹波系数降低,波形变得比较平滑。
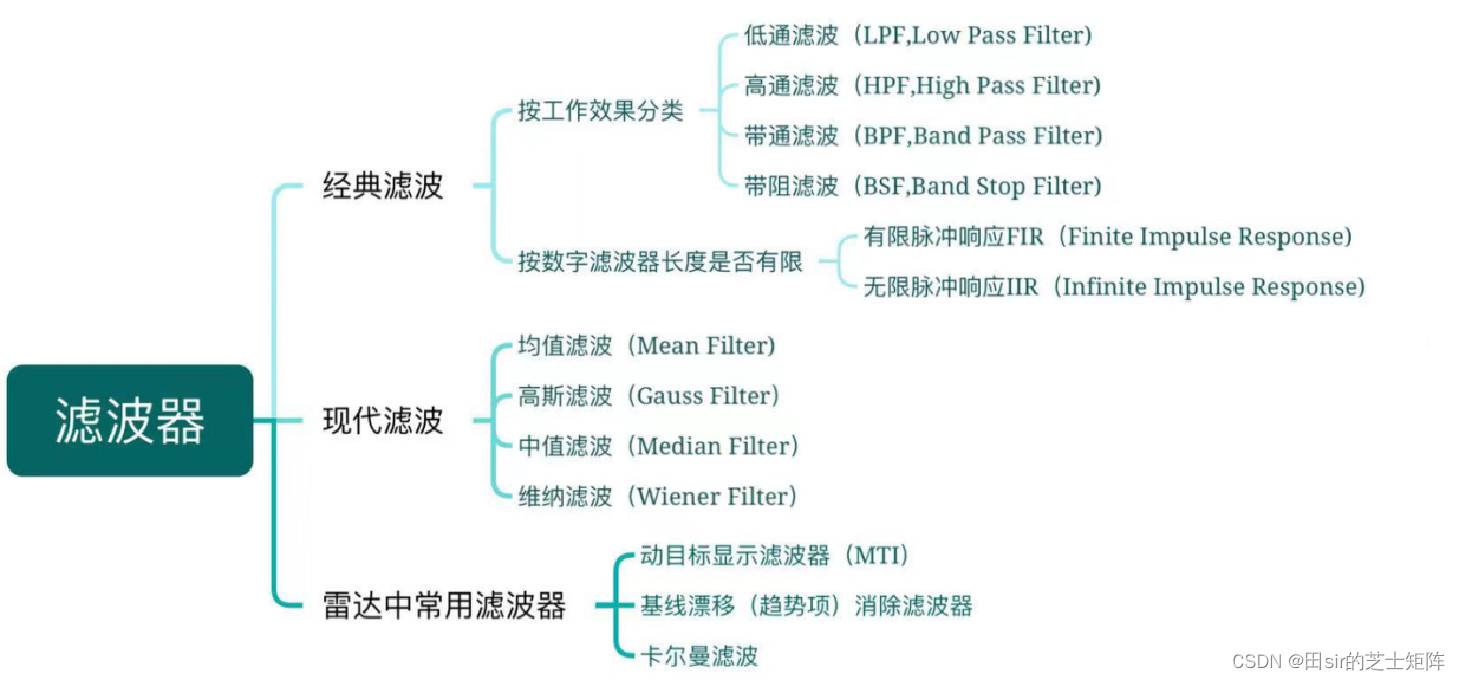
一般滤波器可以分为两类:经典滤波器和现代滤波器:
- 经典滤波器:只允许一定频率范围内的信号成分正常通过,而阻止另一部分频率成分通过的电路,叫做经典滤波器。 经典滤波器通常从频率的视角,留下某些成分,削弱某些成分,达到信号纯化、目标特征提取等目的。
- 现代滤波器:自适应滤波并不针对某一些频段来操作,而是针对从有用目标信号中分离噪声、抑制噪声的目的开展深入研究探讨。显而易见,现代滤波器、自适应滤波器更适用于雷达这样的系统。
对于雷达来说,人们感兴趣的是其能够跟踪目标。但目标的位置、速度、加速度的测量值往往在任何时候都有噪声。卡尔曼滤波利用目标的动态信息,设法去掉噪声的影响,得到一个关于目标位置的好的估计。这个估计可以是对当前目标位置的估计(滤波),也可以是对于将来位置的估计(预测),也可以是对过去位置的估计(插值或平滑)。
二.卡尔曼滤波(Kalman Filter)原理
卡尔曼滤波(Kalman filter)是一种高效率的递归滤波器(自回归滤波器),它能够从一系列的不完全及包含噪声的测量中,估计动态系统的状态。卡尔曼滤波会根据各测量量在不同时间下的值,考虑各时间下的联合分布,再产生对未知变数的估计,因此会比只以单一测量量为基础的估计方式要准确。
以飞机的某一状态为例:

(1)定性理解
卡尔曼滤波主要的工作步骤有两个:预测与更新
- 在预测阶段,滤波器使用上一状态的估计,做出对当前状态的估计。
- 在更新阶段,滤波器利用对当前状态的观测值优化在预测阶段获得的预测值,以获得一个更精确的新估计值。
(2)定量推导
卡尔曼滤波前提假设:
- 假设物体时匀速运动的,即v1=v2
- 假设所有状态(位置)的变化都是线性的
- 噪声服从高斯分布
卡尔曼滤波器核心估计模式:

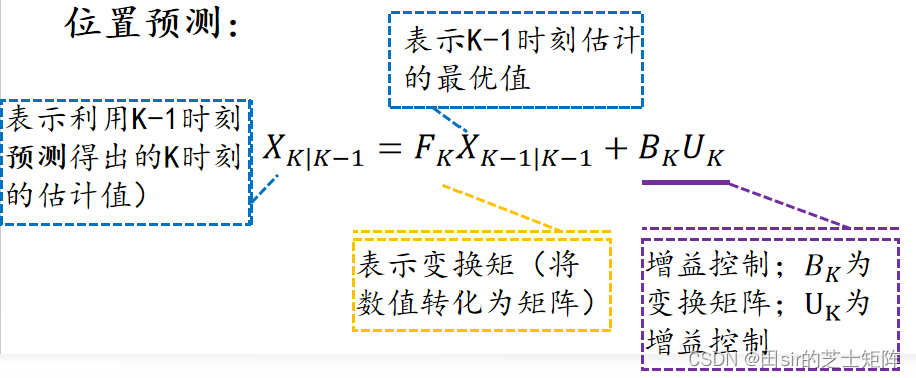
1. 预测阶段
通过第k-1时刻预测出的k时刻估计值 = k-1时刻的最优值+ 控制增益

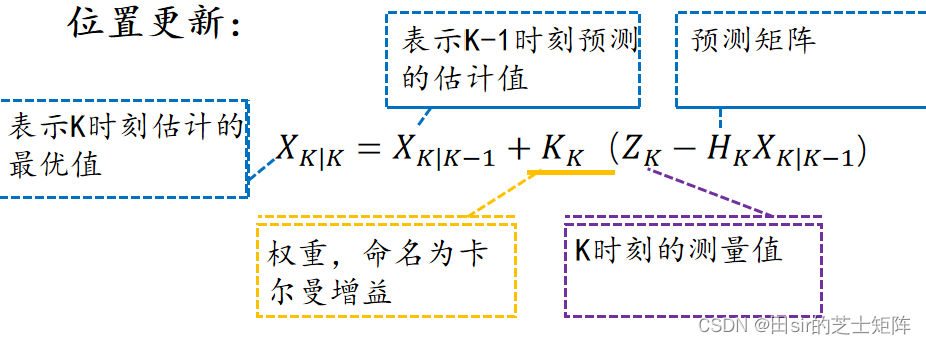
2. 更新阶段
K时刻位置的估计最优值 = 通过k-1时刻的预测k时刻的估计值+因子a ×(测量值-上次估计值)
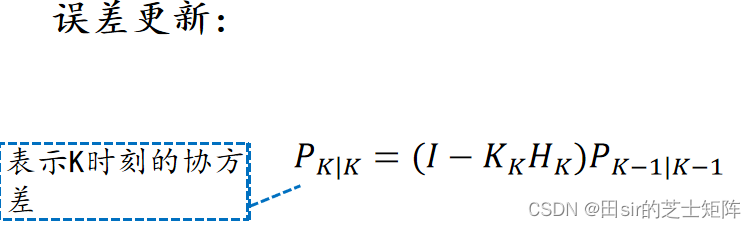
3. 卡尔曼增益
1)卡尔曼增益
其中表示对象噪声的方差矩阵
当前位置状态最优估计:
此时k时刻的位置表达式就是由上一时刻估计的位置与占一定权重的误差(测量值与估计值)所构成的。
2)如何理解卡尔曼增益?
卡尔曼增益实质上这个是用来调节根据上个位置估计出的当前位置值与测量值最终结果中的占比用的。
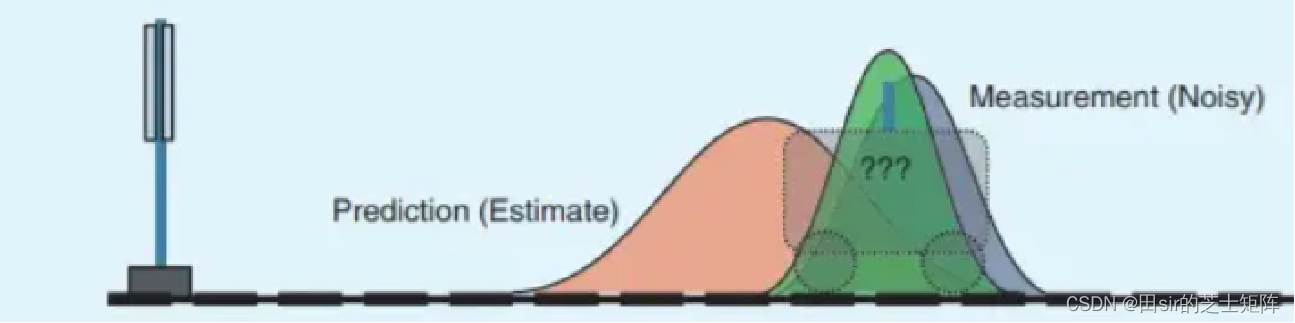
上图中红色的高斯分布表示预测的小车位置; 蓝色的高斯分布表示观测的小车位置; 而融合后,就是绿色的位置;这里只是做了两个高 斯分布的相乘,结果是高斯分布。
三.统计概念理解
(1)马尔科夫链
- 定性理解:某一过程当前的状态仅仅与上一时刻的状态有关,与过去无关
- 结合雷达:当前位置的预测只需要通过上一时刻的位置来预测,不需要更早时刻的数据。
(2)转移矩阵
- 定性理解:矩阵各元素都是非负的,并且各行元素之和等于1,各元素用概率表示,在一定条件下是互相转移的,故称为转移概率矩阵。
- 结合雷达:计算出每一中情况下,从k-1状态达到k状态的概率,所有的概率构成一个转移矩阵。
四.卡尔曼滤波代码(matlab)
function kalman_filter
% 初始化参数
N = 100; % 观测数据长度
dt = 0.1; % 时间间隔
T = 10; % 总时间
x = randn(N, 1); % 初始状态
P = eye(N); % 初始估计协方差
Q = randn(N, N); % 过程噪声协方差
R = randn(N, N); % 观测噪声协方差
K = zeros(N, N); % 卡尔曼增益矩阵
x_est = zeros(N, 1); % 估计状态
P_est = eye(N); % 估计协方差矩阵% 卡尔曼滤波循环
for t = 1:T% 更新过程x_est(t) = x_est(t-1) + dt * (P_est(t-1) * x_est(t-1) + Q(t-1));P_est = P_est - dt * (P_est * x_est(t-1) + R(t-1));K(t) = P_est / (P_est + R(t)); % 卡尔曼增益计算% 预测部分(噪声)数据加上观测值进行修正y = z; % 这里的 z 是实际观测数据,根据你的应用设定,你可能需要使用一个接口或其他方式来获取这个值。y_hat = y - P * K; % 对预测的 y 值进行处理以获取正确的 y 值,这个处理通常包含了一些数学变换。% 使用新的 y 值来更新估计值和协方差矩阵x_est(t) = x_est(t) + K * (y - x_est(t)); % 用观测值更新估计值P_est = (eye(N) - K * P) * P_est; % 用观测噪声更新协方差矩阵
end
end
其中:
N是数据长度,也就是需要在卡尔曼滤波中处理的数据点数量dt是时间间隔T是总时间,也就是需要对数据进行的处理次数x是初始状态,P是初始估计协方差矩阵,Q是过程噪声协方差,R是观测噪声协方差K是卡尔曼增益矩阵,它决定了如何使用观测值来更新估计值和协方差矩阵x_est是估计状态,它是在卡尔曼滤波过程中不断更新的值P_est是估计协方差矩阵,描述了估计状态的精度- 在循环中,首先进行更新过程,然后进行预测部分(噪声)数据加上观测值进行修正,最后使用新的观测值来更新估计值和协方差矩阵。这个过程会重复
T次。








![[图解]SysML和EA建模住宅安全系统-02](https://img-blog.csdnimg.cn/direct/e39683c2350d4b4d92f5424a83977026.png)