题目与题解
参考资料:动态规划总结篇
647. 回文子串
题目链接:647. 回文子串
代码随想录题解:647. 回文子串
视频讲解:动态规划,字符串性质决定了DP数组的定义 | LeetCode:647.回文子串_哔哩哔哩_bilibili
解题思路:
只能想到表面是动态规划,但实际是暴力法的方法。
dp[i]表示包含第i个字符的0-i范围的字符串有几个回文串,dp[i+1]的计算则在dp[i]的基础上增加了新字符后增加的回文串。用isReversed函数判断当前字符串是否为回文串,如果是就在结果上加一。
class Solution {public int countSubstrings(String s) {int[] dp = new int[s.length()];dp[0] = 1;for (int i = 1; i < s.length(); i++) {dp[i] = dp[i-1];for (int j = 0; j <= i; j++) {dp[i] += isReversed(s, j, i) ? 1:0;}}return dp[s.length()-1];}boolean isReversed(String s, int start, int end) {int i = start, j = end;while (i <= j) {if (s.charAt(i) != s.charAt(j)) {return false;}i++;j--;}return true;}
}看完代码随想录之后的想法
二维dp有点难,想不到,记录一下。
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
在确定递推公式时,就要分析如下几种情况。
整体上是两种,就是s[i]与s[j]相等,s[i]与s[j]不相等这两种。
当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况
- 情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
- 情况二:下标i 与 j相差为1,例如aa,也是回文子串
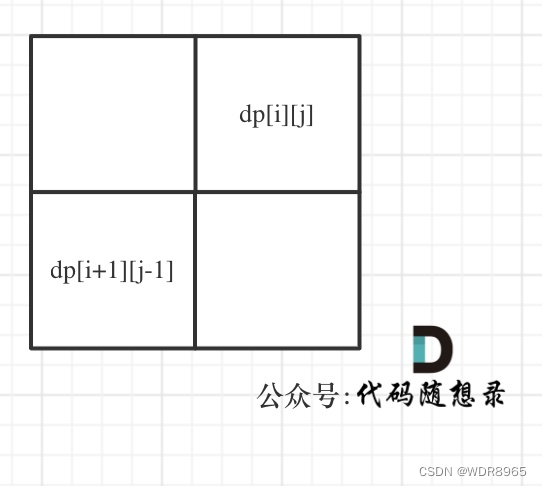
- 情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
初始化dp的值为false。遍历顺序为从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的。
class Solution {public int countSubstrings(String s) {char[] chars = s.toCharArray();int len = chars.length;boolean[][] dp = new boolean[len][len];int result = 0;for (int i = len - 1; i >= 0; i--) {for (int j = i; j < len; j++) {if (chars[i] == chars[j]) {if (j - i <= 1) { // 情况一 和 情况二result++;dp[i][j] = true;} else if (dp[i + 1][j - 1]) { //情况三result++;dp[i][j] = true;}}}}return result;}
}中心法非常巧妙,按顺序遍历每个字符,如果以当前字符为中心有回文,中心字符一定是当前字符,或当前字符和下一个字符。
class Solution {public int countSubstrings(String s) {int len, ans = 0;if (s == null || (len = s.length()) < 1) return 0;//总共有2 * len - 1个中心点for (int i = 0; i < 2 * len - 1; i++) {//通过遍历每个回文中心,向两边扩散,并判断是否回文字串//有两种情况,left == right,right = left + 1,这两种回文中心是不一样的int left = i / 2, right = left + i % 2;while (left >= 0 && right < len && s.charAt(left) == s.charAt(right)) {//如果当前是一个回文串,则记录数量ans++;left--;right++;}}return ans;}
}遇到的困难
这属于不看想不到的题,记住吧。
516.最长回文子序列
题目链接:516.最长回文子序列
代码随想录题解:516.最长回文子序列
视频讲解:动态规划再显神通,LeetCode:516.最长回文子序列_哔哩哔哩_bilibili
解题思路:
不会,看答案
看完代码随想录之后的想法
仍旧是用二维dp,但是定义有点说法,dp[i][j]表示范围在i-j之内的最长回文子序列。
思路跟前一题的二维dp算法有点类似,如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
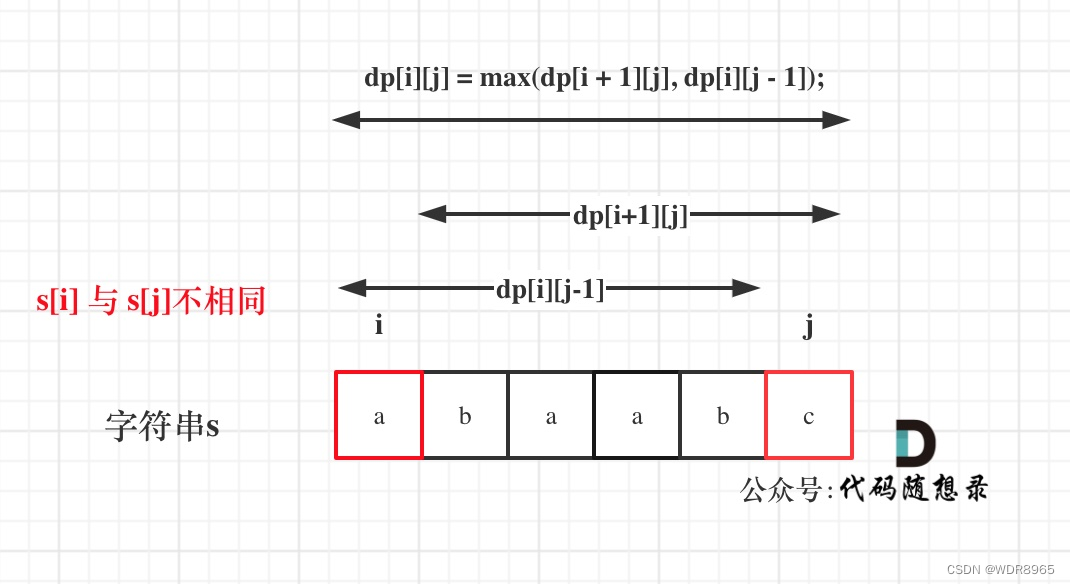
需要手动初始化dp[i][i]为1,表示单字符至少存在一个回文子序列。
根据递推公式可以得到遍历顺序为从下往上从左往右
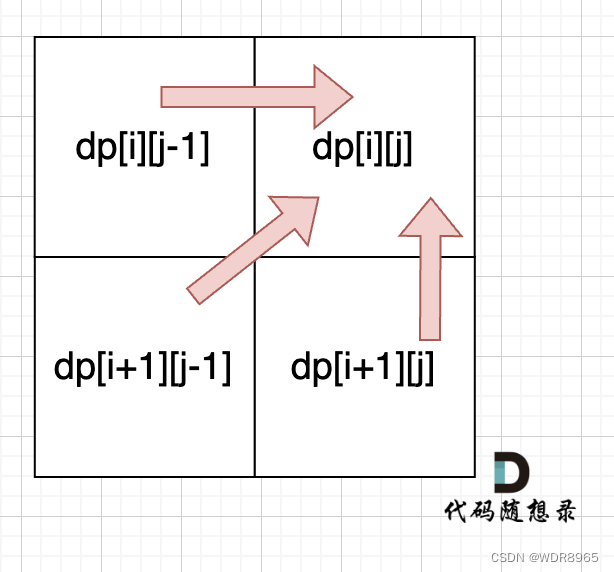
class Solution {public int longestPalindromeSubseq(String s) {int[][] dp = new int[s.length()][s.length()];for (int i = s.length()-1; i >= 0; i--) {dp[i][i] = 1;for (int j = i+1; j < s.length(); j++) {if (s.charAt(i) == s.charAt(j)) {dp[i][j] = dp[i+1][j-1]+2;} else {dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1]);}}}return dp[0][s.length()-1];}
}遇到的困难
动态规划题目过于灵活变化多端把握不住。
今日收获
动态规划结束,灵活的二维动态规划好难。不过碰到这种字符串啦序列的题目,用前后两端的作为计算的start和end还蛮常见的,回溯法里面也有用到,可以记一下。




![[Kotlin]创建一个私有包并使用](https://img-blog.csdnimg.cn/direct/c2c510e486244c47a43bc8bd93c9ff65.png)


![[译文] 恶意代码分析:1.您记事本中的内容是什么?受感染的文本编辑器notepad++](https://img-blog.csdnimg.cn/direct/f615cf28f3084158957e6d5f6e0d1384.png#pic_center)