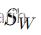线上OJ:
一本通:http://ybt.ssoier.cn:8088/problem_show.php?pid=1971
核心思想:
本题的约束条件有两个:
条件1、colorx = colorz
条件2、x、y、z的坐标满足 y − x = z − y(即 y 在 x 和 z 的中心位置)
第二个约束条件可以理解为, z 到 x 的距离是 y 到 x 的距离的两倍,所以对z暴力枚举时,步长为2的倍数
考场上如果暂时没有更好的想法,可以先把 暴力枚举 写出来。本题的暴力法比较简单,只需要枚举x和z,并且在 枚举z的时候考虑步长为2 即可(这样可以保证x和z中间一定有整数y,就不用再考虑y了)。这样可以快速拿到40%的分数。
解法一、暴力枚举(40%)
#include <bits/stdc++.h>
#define MOD 10007
using namespace std;// 40% 暴力分
int main()
{int n, m, ans = 0;cin >> n >> m;int col[n+5], num[n+5];for(int i = 1; i <= n; i++) scanf("%d", &num[i]);for(int i = 1; i <= n; i++) scanf("%d", &col[i]); for(int x = 1; x <= n; x++)for(int z = x + 2; z <= n; z += 2) // 考虑x和z中间夹一个y,所以每次搜寻z时步长为2{if(col[x] == col[z])ans += (((x + z) % MOD) * ((num[x] + num[z]) % MOD)) % MOD;}printf("%d", ans % MOD); // 最后一次别忘了除模return 0;
}
解法二的核心思想:
思考1、对于分颜色的问题如果正向枚举超时,我们可以尝试用 桶 的方式思考。由于满足 c o l o r x = c o l o r z color_x = color_z colorx=colorz 才进行计算,所以在读入数据时 把相同颜色的色块放入同一个桶 中,这样计算时只需要每个桶内进行枚举判断是否满足 z 到 x 的步长为 2 即可。
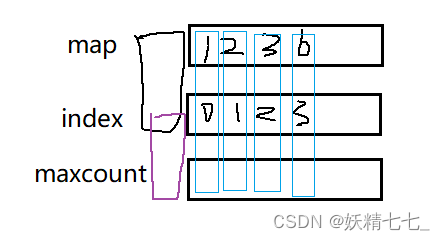
思考2、对于桶内的编号进一步分析。如下图举例,假设蓝色的色块包含序号为1、3、4、5、6、7、12的色块。我们发现满足 z 到 x 的步长为 2 的色块 要么都是偶数 编号,要么都是奇数 编号。如果我们把奇数和偶数的部分再拆成2个小桶,那么在每个小桶内就不需要枚举判断,而是直接遍历计算每个格子即可。本题的最终结果就是每个小桶的结果之和。
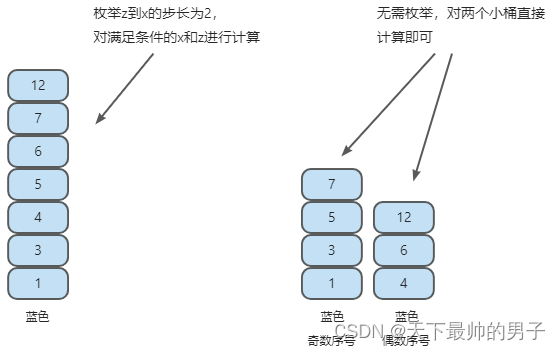
思考3、以上图中蓝色奇数序号的小桶为例,该小桶内的计算公式为,
a n s j = ( x 1 + x 2 ) ∗ ( n u m 1 + n u m 2 ) + ( x 1 + x 3 ) ∗ ( n u m 1 + n u m 3 ) + ( x 1 + x 4 ) ∗ ( n u m 1 + n u m 4 ) ans_j = (x_1+x_2)*(num_1+num_2)+ (x_1+x_3)*(num_1+num_3)+ (x_1+x_4)*(num_1+num_4) ansj=(x1+x2)∗(num1+num2)+(x1+x3)∗(num1+num3)+(x1+x4)∗(num1+num4)
+ ( x 2 + x 3 ) ∗ ( n u m 2 + n u m 3 ) + ( x 2 + x 4 ) ∗ ( n u m 2 + n u m 4 ) \quad \quad \quad + (x_2+x_3)*(num_2+num_3)+ (x_2+x_4)*(num_2+num_4) +(x2+x3)∗(num2+num3)+(x2+x4)∗(num2+num4)
+ ( x 3 + x 4 ) ∗ ( n u m 3 + n u m 4 ) \quad \quad \quad + (x_3+x_4)*(num_3+num_4) +(x3+x4)∗(num3+num4)
= x 1 ∗ ( n u m 1 + n u m 2 ) + x 1 ∗ ( n u m 1 + n u m 3 ) + x 1 ∗ ( n u m 1 + n u m 4 ) \quad \quad = x_1*(num1+num2) + x_1*(num_1+num_3) + x_1*(num_1+num_4) =x1∗(num1+num2)+x1∗(num1+num3)+x1∗(num1+num4)
+ x 2 ∗ ( n u m 1 + n u m 2 ) + x 3 ∗ ( n u m 1 + n u m 3 ) + x 4 ∗ ( n u m 1 + n u m 4 ) \quad \quad \quad + x_2*(num_1+num_2) + x_3*(num_1+num_3) + x_4*(num_1+num_4) +x2∗(num1+num2)+x3∗(num1+num3)+x4∗(num1+num4)
+ x 2 ∗ ( n u m 2 + n u m 3 ) + x 2 ∗ ( n u m 2 + n u m 4 ) \quad \quad \quad + x_2*(num_2+num_3) + x_2*(num_2+num_4) +x2∗(num2+num3)+x2∗(num2+num4)
+ x 3 ∗ ( n u m 2 + n u m 3 ) + x 4 ∗ ( n u m 2 + n u m 4 ) \quad \quad \quad + x_3*(num_2+num_3) + x_4*(num_2+num_4) +x3∗(num2+num3)+x4∗(num2+num4)
+ x 3 ∗ ( n u m 3 + n u m 4 ) + x 4 ∗ ( n u m 3 + n u m 4 ) \quad \quad \quad + x_3*(num_3+num_4) + x_4*(num_3+num_4) +x3∗(num3+num4)+x4∗(num3+num4)
= x 1 ∗ ( n u m 1 + n u m 2 + n u m 1 + n u m 3 + n u m 1 + n u m 4 ) \quad \quad = x_1*(num_1+num_2+num_1+num_3+num_1+num_4) =x1∗(num1+num2+num1+num3+num1+num4)
+ x 2 ∗ ( n u m 1 + n u m 2 + n u m 2 + n u m 3 + n u m 2 + n u m 4 ) \quad \quad \quad + x_2*(num_1+num_2+num_2+num_3+num_2+num_4) +x2∗(num1+num2+num2+num3+num2+num4)
+ x 3 ∗ ( n u m 1 + n u m 3 + n u m 2 + n u m 3 + n u m 3 + n u m 4 ) \quad \quad \quad + x_3*(num_1+num_3+num_2+num_3+num_3+num_4) +x3∗(num1+num3+num2+num3+num3+num4)
+ x 4 ∗ ( n u m 1 + n u m 4 + n u m 2 + n u m 4 + n u m 3 + n u m 4 ) \quad \quad \quad + x_4*(num_1+num_4+num_2+num_4+num_3+num_4) +x4∗(num1+num4+num2+num4+num3+num4)
= x 1 ∗ ( 2 ∗ n u m 1 + n u m 1 + n u m 2 + n u m 3 + n u m 4 ) \quad \quad = x_1*(2*num_1 + num_1+num_2+num_3+num_4) =x1∗(2∗num1+num1+num2+num3+num4)
+ x 2 ∗ ( 2 ∗ n u m 2 + n u m 1 + n u m 2 + n u m 3 + n u m 4 ) \quad \quad \quad + x_2*(2*num_2 + num_1+num_2+num_3+num_4) +x2∗(2∗num2+num1+num2+num3+num4)
+ x 3 ∗ ( 2 ∗ n u m 3 + n u m 1 + n u m 2 + n u m 3 + n u m 4 ) \quad \quad \quad + x_3*(2*num_3 + num_1+num_2+num_3+num_4) +x3∗(2∗num3+num1+num2+num3+num4)
+ x 4 ∗ ( 2 ∗ n u m 4 + n u m 1 + n u m 2 + n u m 3 + n u m 4 ) \quad \quad \quad + x_4*(2*num_4 + num_1+num_2+num_3+num_4) +x4∗(2∗num4+num1+num2+num3+num4)
所以,如果一个小桶内有n个格子,则上述公式可以调整为
a n s j = x 1 ∗ [ ( n − 2 ) ∗ n u m 1 + n u m 1 + n u m 2 + n u m 3 + . . . . . . + n u m n ] ans_j = x_1*[(n-2)*num_1 + num_1+num_2+num_3+......+num_n] ansj=x1∗[(n−2)∗num1+num1+num2+num3+......+numn]
+ x 2 ∗ [ ( n − 2 ) ∗ n u m 2 + n u m 1 + n u m 2 + n u m 3 + . . . . . . + n u m n ] \quad \quad \quad + x_2*[(n-2)*num_2 + num_1+num_2+num_3+......+num_n] +x2∗[(n−2)∗num2+num1+num2+num3+......+numn]
+ x 3 ∗ [ ( n − 2 ) ∗ n u m 3 + n u m 1 + n u m 2 + n u m 3 + . . . . . . + n u m n ] \quad \quad \quad + x_3*[(n-2)*num_3 + num_1+num_2+num_3+......+num_n] +x3∗[(n−2)∗num3+num1+num2+num3+......+numn]
. . . . . . \quad \quad \quad ...... ......
+ x n ∗ [ ( n − 2 ) ∗ n u m 4 + n u m 1 + n u m 2 + n u m 3 + . . . . . . + n u m n ] \quad \quad \quad + x_n*[(n-2)*num_4 + num_1+num_2+num_3+......+num_n] +xn∗[(n−2)∗num4+num1+num2+num3+......+numn]
我们发现, n u m 1 + n u m 2 + n u m 3 + . . . . . . + n u m n num_1+num_2+num_3+......+num_n num1+num2+num3+......+numn 在初始读入数据时可以顺便计算出来(前缀和),将其表示为 ∑ ( n u m i ) \sum(num_i) ∑(numi),表示该小桶中所有格子的数值之和。
a n s j = x 1 ∗ [ ( n − 2 ) ∗ n u m 1 + ∑ ( n u m i ) ] + x 2 ∗ [ ( n − 2 ) ∗ n u m 2 + ∑ ( n u m i ) ] + . . . . . . ans_j = x_1*[(n-2)*num1 + \sum(num_i)] + x_2*[(n-2)*num2 + \sum(num_i)] + ...... ansj=x1∗[(n−2)∗num1+∑(numi)]+x2∗[(n−2)∗num2+∑(numi)]+......
+ x n ∗ [ ( n − 2 ) ∗ n u m n + ∑ ( n u m i ) ] \quad \quad \quad + x_n*[(n-2)*num_n + \sum(num_i)] +xn∗[(n−2)∗numn+∑(numi)]
= x 1 ∗ ( n − 2 ) ∗ n u m 1 + x 1 ∗ ∑ ( n u m i ) + x 2 ∗ [ ( n − 2 ) ∗ n u m 2 + x 2 ∗ ∑ ( n u m i ) + . . . . . . \quad \quad = x_1*(n-2)*num1 +x_1*\sum(num_i) + x_2*[(n-2)*num2 + x_2* \sum(num_i) +...... =x1∗(n−2)∗num1+x1∗∑(numi)+x2∗[(n−2)∗num2+x2∗∑(numi)+......
+ x n ∗ ( n − 2 ) ∗ n u m n + x n ∗ ∑ ( n u m i \quad \quad \quad + x_n*(n-2)*num_n + x_n*\sum(num_i +xn∗(n−2)∗numn+xn∗∑(numi
= ( n − 2 ) ∗ x 1 ∗ n u m 1 + ( n − 2 ) ∗ x 2 ∗ n u m 2 + . . . . . . + ( n − 2 ) ∗ x n ∗ n u m n \quad \quad = (n-2)*x_1*num1 + (n-2)*x_2*num2 + ...... + (n-2)*x_n*num_n =(n−2)∗x1∗num1+(n−2)∗x2∗num2+......+(n−2)∗xn∗numn
+ ( x 1 + x 2 + . . . . . . + x n ) ∗ ∑ ( n u m i ) \quad \quad \quad +(x_1+x_2+......+x_n)*\sum(num_i) +(x1+x2+......+xn)∗∑(numi)
上式中,(n-2)表示该小桶中格子的数量减2。这个 n 可以在初始 读入数据时先行累加 出来。
因此我们发现,在计算时每一个格子真正参与的部分是:
( n − 2 ) ∗ x i ∗ n u m i + x i ∗ ∑ ( n u m i ) (n-2) * x_i * num_i + x_i * \sum(num_i) (n−2)∗xi∗numi+xi∗∑(numi)
在上式中, x i x_i xi 是格子的编号, n u m i num_i numi 是格子的数值,(n-2)是格子所属小桶中格子的数量-2(可提前计算), ∑ ( n u m i ) \sum(num_i) ∑(numi) 是格子所属小桶中所有格子的数值之和(可提前计算)。至此,已不需要枚举任何数值。
同时, 每个格子不管归属于哪一个小桶,都要参与一次计算,所以把每一个格子都进行一次计算,所得到的总和就是最终的结果。
题解代码:
#include <bits/stdc++.h>
#define MOD 10007
#define MAXN 100005
using namespace std;const int N = 100010, mod = 10007;int num[MAXN], col[MAXN]; // num[i]表示第i个格子的数字,col[i]表示第i个格子的颜色//cnt[i][0]表示颜色为i、编号为偶数的格子的个数
int sum[MAXN][2], cnt[MAXN][2]; // sum[i][0]表示颜色为i、编号为偶数的格子上数字的∑wi// sum[i][1]表示颜色为i、编号为奇数的格子上数字的∑wi// cnt[i][0]表示颜色为i、编号为偶数的格子的个数// cnt[i][1]表示颜色为i、编号为奇数的格子的个数int main()
{int n, m, ans = 0;cin >> n >> m;for(int i = 1; i <= n; i ++) scanf("%d", &num[i]);for(int i = 1; i <= n; i ++){scanf("%d", &col[i]); // 根据格子的颜色以及奇偶,更新对应桶的∑wi。每个颜色分为奇偶两桶sum[col[i]][i % 2] = (sum[col[i]][i % 2] + num[i]) % MOD;// 根据格子的颜色以及奇偶,更新对应桶内的格子个数,用于n-2时使用cnt[col[i]][i % 2] ++;}for(int i = 1; i <= n; i ++)ans = (ans + i * ((cnt[col[i]][i % 2] - 2) * num[i] % MOD + sum[col[i]][i % 2])) % MOD;printf("%d", ans);return 0;
}






![[Meachines][Easy]Bizness](https://img-blog.csdnimg.cn/img_convert/f0c3b43cdf7c18f876752b72612cfd06.jpeg)